咸阳市渭城区第二初级中学教学楼设计外文翻译资料

英语原文共 13 页，剩余内容已隐藏，支付完成后下载完整资料

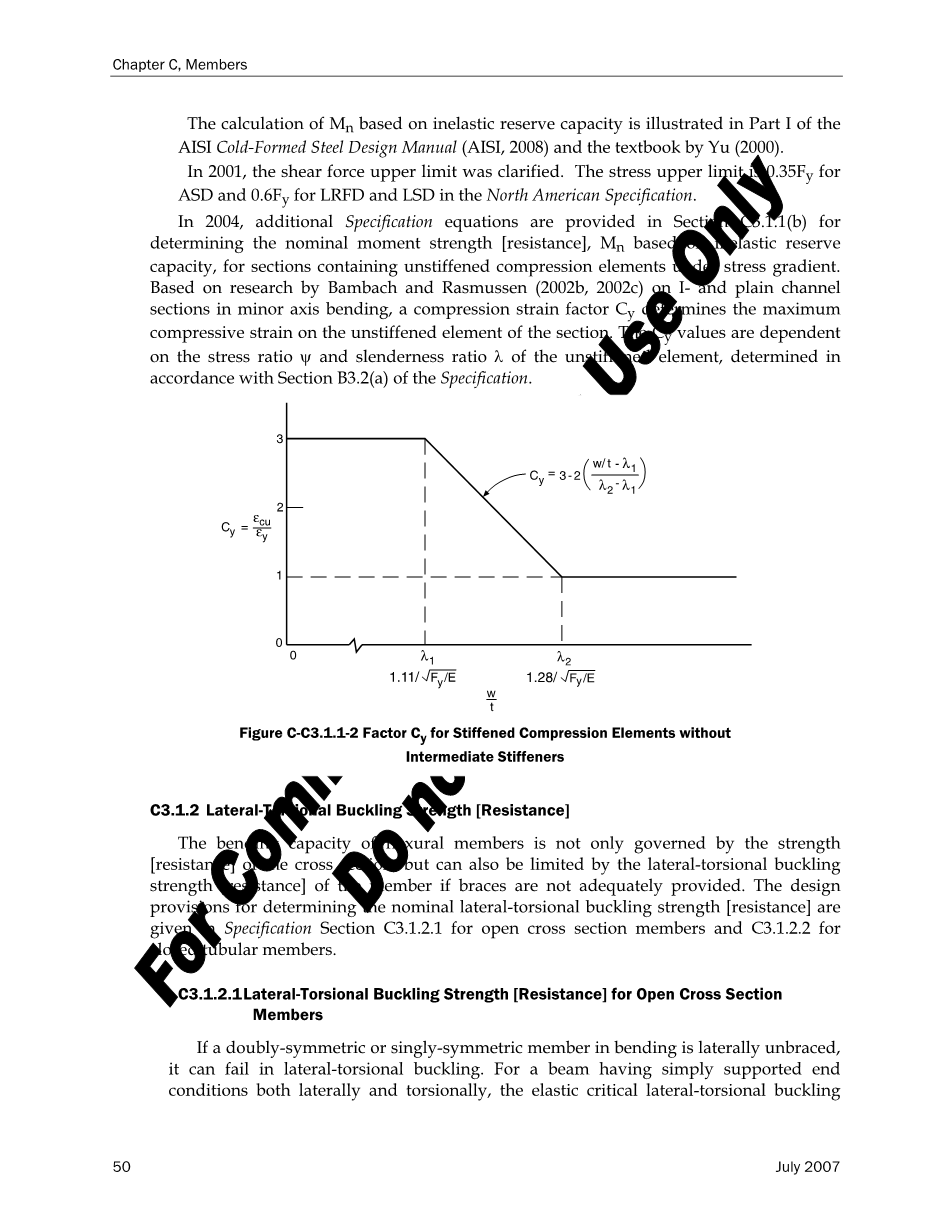
美国钢结构学会冷弯型钢设计手册（美国钢结构学会2008）和余教授编写的教科书（2000）的第一部分说明了关于非弹性储备能力的M_n的计算。在2001，已经清楚了剪力上限值。在北美规范中，对于ASD其应力上限值是0.35f_y，而对于LRFD和LSD则是0.6f_y。在2004年，在C3.1.1（b）部分中又增加了规范方程，可用来确定在应力梯度下对于非压缩杆件的非弹性储备能力的力矩值的M_n。在本巴赫和拉斯姆森（2002b，2002C）在对短轴弯曲中的I型钢和普通槽钢的研究中，压缩应变系数C_y决定了刚性元件的最大压缩应变值。而C_y取决于刚性元件的应力比和长细比，与规范B部分3.2(a)的说明相一致。

图C-C3.1.1-2无中间加劲肋受压元件的系数C_y

C3.1.2横向扭转屈曲强度

受弯构件的抗弯承载力不仅受截面强度的影响，而且如果没有合适的支撑，也会受到构件的横向扭转屈曲强度的影响。对开口截面的侧向扭转屈曲强度规范C3.1.2.1有说明,而对封闭的管状构件规范C3.1.2.2有所规定。

C3.1.2.1开口截面构件的横向扭转屈曲强度

如果一个双对称或单轴对称的受弯构件是受到横向支撑的话，它会由于侧扭屈曲而破坏。对于一个受到横向和扭转的简支端梁，其弹性弯扭屈曲临界应力可以通过方程C-C3.1.2.1-1确定。

对于其他条件的简支端构件，方程C-C3.1.2.1-1可以变形为方程C-C3.1.2.1-1a（加兰博斯，1998）

上述方程中，K_y和K_t是有效长度系数，L_y和L_t是y轴方向弯绕且受扭的杆端自由长度，另外，E是弹性模量，G是剪切模量，S_f是极端受压的刚性构件的弹性截面模量，I_y是绕Y轴的惯性矩，C_w是扭转翘曲常数，J是圣维南扭转常数，L是自由杆端长度。

对于受到横向和扭转简支端条件的平翼缘I型截面构件，方程C-C3.1.2.1-2可以用来计算弹性屈曲临界应力（温特，1947a；余教授，2000）：

方程C-C3.1.2.1-2中，平方根下的第一项表示构件的横向抗弯刚度，和第二项代表圣维南扭转刚度。对于薄壁冷弯型钢部分，第一个项的值大小通常大幅度超过第二项。

对于非平翼缘简支端Ｉ型截面构件，下列是由温特推导的求其横向扭转屈曲应力的方程（温特，1943）：

式中I_yC和I_yt是平行于腹板形心轴的压缩惯性矩和全截面拉伸转动惯量。其他的符号如之前所定义的。对于平翼缘构件，I_yC =I_yt =I_y/2，方程Ｃ-Ｃ3.1.2.1-2和Ｃ-Ｃ3.1.2.1-3情况也是如此。

对于其他条件的简支端构件，方程Ｃ-Ｃ3.1.2.1-3可以变形为方程Ｃ-Ｃ3.1.2.1-3a。

在Ｃ-Ｃ3.1.2.1-3a方程中，平方根中第二项代表圣维南扭转刚度。因此，可以考虑I_y =I_yC I_yt，省略4GJ(K_tL_t)²/(pi;²I_yEd²)这一项，方程Ｃ-Ｃ3.1.2.1-3a可简化为公式Ｃ-Ｃ3.1.2.1-4所示。

方程Ｃ-Ｃ3.1.2.1-4是在均匀弯矩基础上推算的，对于其他的弯矩情况不是精确的，为此在的右边乘以弯曲系数C_b进行修正。考虑到非均匀弯矩的情况，将符号改为F_e，即：

式中C_b是弯曲系数，该值可以按规范来取，也可以按下面式子计算：

式中M1是自由杆端的较小弯矩值，M2是自由杆端的较大弯矩值。

1968，1980，1986，和1991版本的美国钢结构学会规范使用得都是上述方程。因为只有对直线弯矩图适用，所以方程Ｃ-Ｃ3.1.2.1-6 C_b的计算由下面的方程来完成，并保留在1996版美国钢结构学会规范这个版本中：

M_max:自由杆段的最大弯矩绝对值

M_A: 自由杆段的四分之一处弯矩绝对值

M_B: 自由杆段中心线上的弯矩绝对值

M_C: 自由杆段四分之三处的弯矩绝对值

图Ｃ-Ｃ3.1.2.1-1：C_b的直线弯矩图

方程Ｃ-Ｃ3.1.2.1-7是由柯比和内瑟科特（1979）推导出来的，可用于在自由杆端各种形状的弯矩图。对于受弯固定端构件和不是直线型的弯矩图，它提供了更精确的解决方法。这个方程是同样被用于美国国家标准学会 /美国钢结构学会S360中（美国钢结构学会，2005）。

图Ｃ-Ｃ3.1.2.1-1展示方程Ｃ-Ｃ3.1.2.1-6和Ｃ-Ｃ3.1.2.1-7在直线弯矩图中的差异。

在2001年，因为方程Ｃ-Ｃ3.1.2.1-5，y轴方向的有效长度系数K_y被加入到方程Ｃ3.1.2.1-14和方程Ｃ3.1.2.1-15中。这K_y系数不仅仅适用于简支杆端条件的。此外，自从1968版美国钢结构学会规范后，方程Ｃ3.1.2.1-14应用于单轴对称的C型截面和I型截面的设计计算，而自从1996版美国钢结构学会规范后，方程C3.1.2.1-15可用于Z型截面的设计计算。

同样在2001年，在规范C5部分由于不考虑轴向荷载和弯矩，则C_b按规范统一取值。这个规定是正确的，因为在规范C5部分中的 C_b和C_m是杆件弯矩梯度的调整值，C_b按规范统一取值是偏于安全的。当弯矩是不连续的而且C_m调节了构件P-二阶的级数，则C_b是侧向扭转屈曲的临界弯矩调整值。因为这两个是独立的量，所以更适合用C_b和C_m这两个量计算在组合荷载下的杆件，但是，C_b仍然按规范统一取值。

应该指出的是，当计算理论屈曲应力时小于或等于比例极限时，方程Ｃ-Ｃ3.1.2.1-1a和Ｃ-Ｃ3.1.2.1-5只适用于冷弯型钢构件，当计算的应力超过比例极限时，梁将受非弹性屈曲控制。非弹性屈曲应力F_C用以下方程Ｃ-Ｃ3.1.2.1-8计算（余教授，2000）：

式中F_C是弹性临界侧向扭转屈曲应力

1968，1980年和1986年版的美国钢结构学会规范中方程Ｃ-Ｃ3.1.2.1-5 和Ｃ-Ｃ3.1.2.1-8的K_y＝1.0及L_y = L就可以得到I型截面构件横向扭转屈曲的许用应力设计方程。在1986年版的美国钢结构学会规范中，除了方程Ｃ-Ｃ3.1.2.1-5 和 Ｃ-Ｃ3.1.2.1-8可以测定临界应力，更多的设计方程（方程Ｃ3.1.2.1 4，Ｃ3.1.2.1-5，和Ｃ3.1.2.1-10）可用来计算弹性临界应力。这些方程是由佩科滋，温特和雪拉比就偏心荷载下薄壁截面弯扭屈曲的研究而来的。这些通用的设计方程可以用于单轴对称，双轴对称和点对称截面。因此，弹性临界横向扭转屈曲应力可由以下方程计算：

式中和是弹性屈曲应力正如规范方程3.1.2.1-8和C3.1.2.1-9定义。

应该指出的是，如平翼缘的Z型截面等点对称截面的横向抗弯强度比双轴对称或单轴对称截面低，规范中已有一个设计方法，在这方法中弹性屈曲临界应力取I型构件弹性屈曲临界应力值的一半。

对于非弹性屈曲临界应力，在1986版美国钢结构学会规范C3.1.2(a)中，下面的公式用于计算临界弯矩值，而不是用方程Ｃ-Ｃ3.1.2.1-8：

其中（M_Cr）_ｅ是弹性临界屈曲弯矩值。在1996年，在美国钢结构学会规范C3.1.2.1(a)部分中，对于单轴、双轴和点对称的基本非弹性弯扭屈曲曲线重新改成与规范C3.1.2.1(b)中的I型、Z型截面的非弹性弯扭屈曲曲线一样。方程Ｃ-Ｃ3.1.2.1-8曲线的一般形状与前版的规范一致（美国钢结构学会 1986）：

图Ｃ-Ｃ3.1.2.1-2侧向扭转屈曲应力

规范Ｃ3.1.2.1指出，在弹性应力达到0.56前发生的是横向扭转屈曲。从0.56F_y到（10/9）F_y的约翰逊抛物线段是非弹性区。（10/9）这个因子是在受弯截面弹塑性状态下求得的（嘉兰博思，1963）。曲线中的平台状态是由于极限应力最大值为F_y而产生的，这样可以使因横向扭转不稳定无应力损失情况下计算最大自由长度。最大自由长度可以在方程 Ｃ-Ｃ3.1.2.1-8中设F_y=F_c而计算。

梁柱（佩科兹和苏美尔，1992）和墙体立柱（牛和佩科兹，1994）的研究已证实单轴，双轴和点对称截面的弹性弯扭屈曲曲线自由化。

Ｃ-Ｃ3.1.2.1-2示图展示的是弹性和非弹性弯扭屈曲临界应力强度。只要自由长度L小于L_u，横向扭转屈曲都不需要考虑，其中L_ｕ是设F_e= 2.78Ｆ_ｙ和Ｌ_ｕ=L_y=L_t来确定的。L_u也可以使用下面给出的表达式计算（美国钢结构学会， 1996）：

（a）对于单轴、双轴和点对称截面：

其中：

当为单、双对称截面

当为点对称截面

（b）对于垂直I型、C型或Z型构件的腹板质心轴线受弯，由以下方程来代替（a）（美国钢结构学会，1996）情况来计算：

对双对称的I字型截面和单对称的C型截面：

对于点对称Z型截面：

对于自由长度Lle;L_ｕ的构件，或弹性弯扭屈曲应力F_ege;2.78Ｆ_ｙ，抗弯强度按照Ｃ3.1.1（a）来计算。

以上讨论仅解决了局部稳定梁的横向扭转屈曲强度。对于局部失稳梁，受压构件的局部屈曲和构件整体的弯扭屈曲的相互作用可能导致构件横向扭转屈曲强度降低。规范Ｃ3.1.2.1中用有效截面的弹性模量SC来考虑临界弯矩下局部屈曲的影响，即：

式中：

FC：弹性或非弹性临界弯扭屈曲应力

SC：应力F_C达到极限压缩状态时计算的有效截面的弹性截面模数

使用上述定义计算时，阻力系数b = 0.90，beta;值取值为2.4~3.8

艾利福瑞特、普特和海恩斯（1992）的研究表明，当中心两支撑间距离定义为自由长度时，对于只有一个跨中支撑的，规范C3.1.2.1方程可以应用。但是两个或两个以上的跨中支撑，该方程将不适合。

上述研究（艾利福瑞特、普特和海恩斯，1992）和卡瓦拿盖和艾利福瑞特研究（1993，1994）已经表明，单独一根的桁架梁，没有屋面和覆盖物，可能在支称之间由于横向扭转屈曲或是扭曲屈曲亦或是在支撑点附近而破坏。见规范 C3.1.4畸变屈曲强度的注释。

图C-C3.1.2.1-3组合板加劲肋截面

图C-C3.1.2.1-4 U型梁的横向屈曲

上面讨论的问题是解决I型截面、C型截面和Z型截面构件单位扭转或横向单位位移时的侧扭屈曲。但这不适于如C-C3.1.2.1-3所示的U型梁和复合板加劲肋的截面情况。对于这种情况，当截面受到如下受荷形式，即构件加劲肋的边缘板受压，梁翼缘受拉而不发生横向侧移时；受压翼缘往往会在横向方向上屈曲，同时腹板发生平面外弯曲，如图C-C3.1.2.1-4所示，除非支撑的强度满足。

U形梁横向屈曲的精确分析是比较复杂的。受压翼缘和腹板的受压部分不仅如弹性基础上的柱一样复杂，而且受翼缘扭转作用的弱化影响也比较复杂。因此，在美国钢结构学会冷弯型钢结构设计手册（美国钢结构学会 2008）的第五部分第2节所述的设计程序（补充资料）是基于道提的简化分析后来确定无支撑的横向受压翼缘的的公称应力值。

在1964年，豪斯勒提出了严格的方法来确定弹性稳定梁的强度（豪斯勒，1964）。在他的方法中，豪斯勒也将无支撑的受压翼缘视作为弹性基础上的柱而且他的方法更严谨。

豪斯勒的方法和道提的简化方法的比较表明，后者可能提供一个较低的临界应力值。

横向无支撑受压翼缘的另外一个研究是在康奈尔大学（石瑞特和佩科兹，1992，1994和1995）进行的。给出了一种用于确定的直立缝屋面板的畸变屈曲强度分析方法。大量的预测值与实验结果进行了比较。

C3.1.2.2封闭箱形构件横向扭转屈曲强度

由于封闭的箱形截面的抗扭转刚度大，在经典的设计考虑中横向扭转屈曲不是关键的，即使是受弯的长轴。当不大于L_u时

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[140559]，资料为PDF文档或Word文档，PDF文档可免费转换为Word