基于中空纳米粒子γ-Al2O3的纳米流体的导热系数以及界面热阻的影响外文翻译资料

英语原文共 6 页，剩余内容已隐藏，支付完成后下载完整资料

基于中空纳米粒子gamma;-Al₂O₃的纳米流体的导热系数以及界面热阻的影响

M.A.Serebryakova, A.V.Zaikovskii, S.Z.Sakhapov, D.V.Smovzh, G.I.Sukhinin, S.A.Novopashin

Kutateladze Institute of Thermophysics, Novosibirsk, Russia

关键词：导热系数 纳米流体 卡皮查界面热阻 液固界面

摘要

本文介绍了基于中空纳米颗粒的纳米流体导热系数的理论和实验研究结果。通过对中空Al₂O₃纳米颗粒在水、乙二醇和异丙醇中的实验，研究了纳米流体的导热系数。该实验是在纳米颗粒体积浓度为2.2%时进行的，导热系数采用非稳态热丝法进行测量。结果发现对于所有纳米流体，获得的热导率与体积浓度的相关性给出的值低于麦克斯韦理论获得的值。分析表明，在这些实验条件下存在空腔，因而不能用该理论解释观察到的结果。基于实验数据与理论的比较，得出了纳米颗粒-液体界面卡皮查接触热阻的最终值。卡皮查接触热阻是针对纳米颗粒材料和所用基本流体之间的界面进行估算的。

1. 引言

纳米流体是包含纳米尺度范围的液体和固体颗粒的两相介质。纳米流体研究引起了人们的兴趣，因为纳米颗粒可以显著的改变基础流体的热物理性质[1]。至今已经进行了许多理论和实验研究[2–16]，理论和实验结果已经得到推广[17–31]。深入的研究表明，经典麦克斯韦理论描述了低浓度球形纳米颗粒下纳米流体的热导率[32]，提出理论模型；他们不仅考虑了依赖于纳米颗粒的体积浓度，还考虑了布朗运动对纳米颗粒的影响、纳米颗粒的形状、导热系数对温度的依赖性、系统的表面电荷和PH值、以及卡皮查接触热阻的贡献[17,18]。注意到他们的研究虽然对结果进行了分析，但大多数实验工作都没有考虑到卡皮查接触热阻的作用[33]。

应该注意的是纳米级别固体颗粒的导热系数在理论描述上发生了重大的变化[34,35]。当描述悬浮液的导热系数时，纳米颗粒的实际导热系数还是一个未知的值，严格的分析需要额外的确定这个值。如果颗粒材料的导热系数大大超过液体的导热系数（一般来说，固体的导热系数比液体导热系数高2-3个数量级），方程式就可以简化，其中纳米颗粒的实际导热系数排除在外。在低浓度的球形纳米颗粒，他们的体积分数、卡皮查接触热阻、纳米颗粒半径和液体导热率[36]是决定参数。

卡皮查热阻导致两个不同材料的界面的温度跳跃，与热通量成正比。这种效应的大小取决于温度和材料特性[35,37–39]。对于接触的固体材料，即使是在微米级，表面热阻也变得很大，这对MEMS技术[40–42]很重要。因为流体的导热系数比固体低2-3个数量级，在向纳米级过渡时卡皮特热跳跃变得很重要。纳米流体热接触热阻在热过程中影响的理论问题在一些研究中已经解决[43–47]。无量纲参数gamma;=GK_f/b决定了卡皮查表面热阻分布，其中b是纳米粒子半径，K_f是基本流体的导热系数，G是颗粒材料和基本流体的接触热阻。这个无量纲参数表征了球形颗粒与周围环境之间的热传递[47]。

在液-固界面处的热跳跃可以通过实验测得[48,49]，也可以通过计算得到，例如通过分子动力学模拟计算[50–54]。当系统有几个界面时，卡皮查热阻对导热系数的作用可能很大，例如在基于核-壳颗粒的纳米流体中。基于核-壳颗粒的悬浮液中导热系数的问题，在排除卡皮查热跳跃后已经得到解决[55]。

本文通过实验研究了基于中空氧化铝纳米粒子和各种基本流体：水、乙二醇和异丙醇对纳米流体的导热系数。通过对基于中空纳米颗粒的纳米流体的导热系数研究，考虑了卡皮查热阻的作用。将实验数据与理论分析的结果进行比较[19]。在总结数十个研究小组的结果后得出结论，纳米流体的导热系数是由麦克斯韦理论描述的，理论分析没有考虑到布朗运动[16]和热量波动[35,56]的影响。纳米颗粒聚集[57]；相关层的影响；根据声子的玻尔兹曼方程改变导热率的机制[35,56,58]，弹道和弹道扩散传热[59]。理论上的分析是基于卡皮查热阻的经典热传导方程，假设纳米颗粒的浓度很低，纳米颗粒材料的导热系数远高于基液的导热系数。

2实验

氧化铝中空纳米颗粒是由等离子弧法[60]合成的，将铝-石墨电极喷入氦介质中，然后在950℃的空气中退火。XRD分析表明该材料是Al₂O₃具有gamma;修饰的晶体结构[60]。根据透射电子显微镜拍摄的照片，该材料呈现中空纳米颗粒，其形状接近球形，典型的尺寸为10纳米。（图1）

图1.Al₂O₃中空纳米颗粒

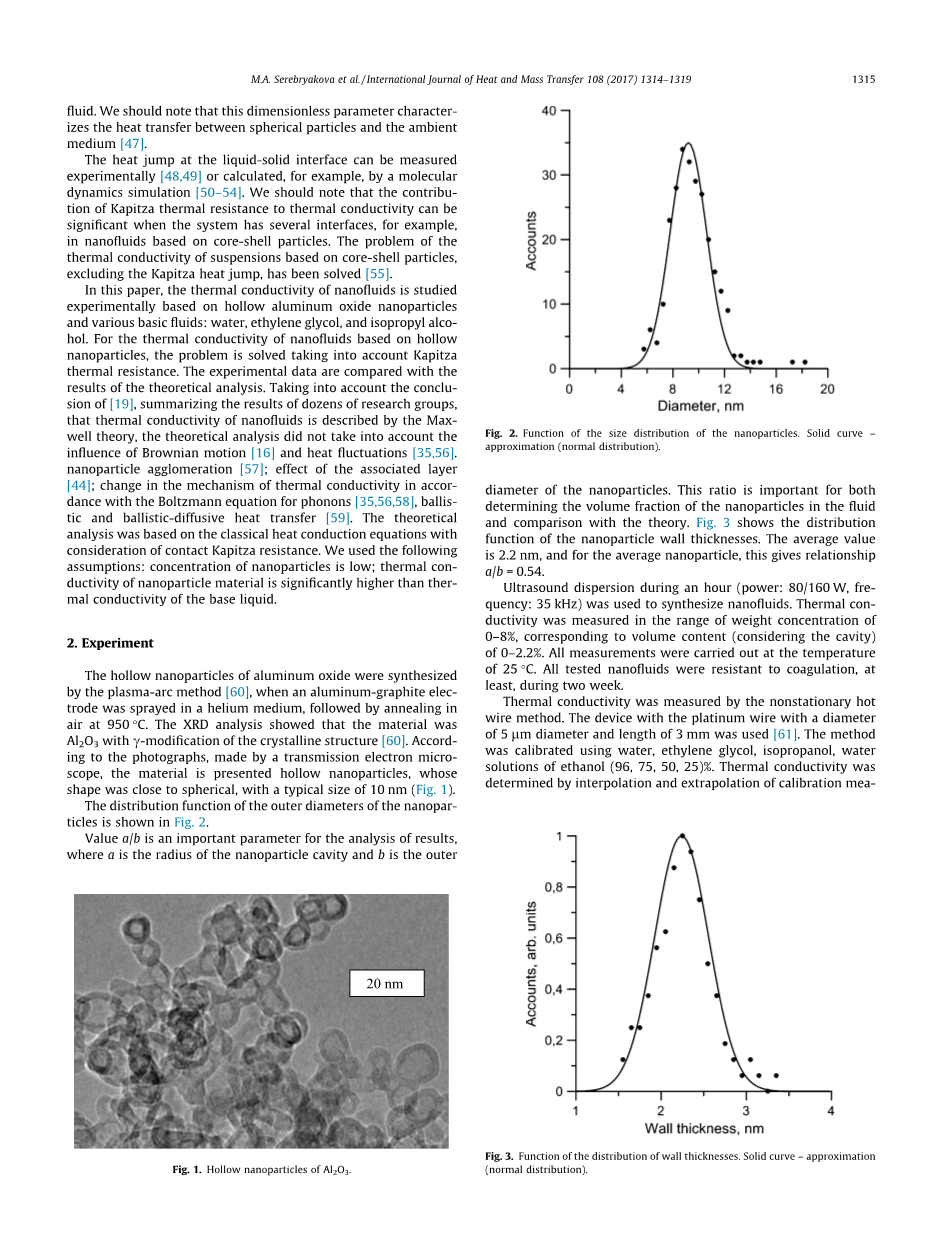
纳米颗粒外径的分布函数如图2所示

图2.纳米颗粒尺寸分布的函数。固体曲线近似(正态分布)

值a/b是分析结果的重要参数，其中a是纳米颗粒腔的半径，b是外部纳米颗粒的直径。这个比率对确定流体中纳米颗粒的体积分数以及与理论进行比较都很重要。图3显示了纳米颗粒壁厚的分布函数。平均值是2.2nm，对于平均纳米颗粒，这给出了关系a/b=0.54。

图3.壁厚分布的函数。固体曲线近似(正态分布)

用超声波持续一个小时的分散（功率：80/160W,频率：35KHZ）来合成纳米流体。在质量浓度为0-8%的条件下测量导热系数，此时相应的体积含量为0-2.2%（考虑空腔）。所有的测量都在25℃的温度下进行，所有测试用的纳米流体至少在两周内抗凝。

导热系数是通过非稳态热丝法测得的。该装置采用的铂丝直径为5um，长度为3mm[61]。这种方法用水、乙二醇、异丙醇、乙醇的水溶液（96,75,50,25%）来校准。导热系数是通过校准测量的插值和外推确定的。为了达到要求的准确度，在每个实验点进行几个系列的25次实验。这样使准确度可达到0.3%。

3、理论

基于中空纳米颗粒的纳米流体的导热系数问题，在排除液-粒表面界面处的卡皮查热跳跃后已经得到解决[55]。在本文中，我们考虑接触热阻的影响。首先，我们解决了关于液体中核-壳颗粒的温度分布问题。

考虑到在极限温度下的线性分布（恒定的温度梯度）：▽=A=常数[62]。用指数p，s和f表示粒子核、壳和流体。因此，导热系数在这些区域分别为K_p、K_s和K_f。假设原子核的半径等于a，外壳的半径为b。在标准的边界条件下，温度平等并且在接触面上的热量流动连续。我们发现可以用以下公式表示温度的分布：

用麦克斯韦法[32]，纳米流体的导热系数可以用以下关系式确定：

这里的K_f和K_nf分别表示的是基本流体的导热系数和纳米流体的导热系数，phi;表示的是纳米颗粒的体积含量。考虑到粒子-液体界面的卡皮查热跳跃，给出以下边界条件：

其中G表征的是界面上温度跳跃的值。

为了找到解决方案，通过引入传导率比值alpha;=K_p/K_f,和beta;=K_s/K_f来计算C_f。无量纲参数gamma;=GK_f/b表征的是表面热阻。利用边界条件，可以得出未知系数的值。具体而言，如下：

其中引入phi;：

通过将公式（3）中C_f/b³代入到公式（2）中，得到了必要的解。因此，由核-壳颗粒组成的纳米流体的传导率和颗粒-液体边界上的表面热阻取决于以下五个参数的值：phi;,（a/b）,alpha;=K_p/K_f,beta;=K_s/K_f和gamma;。

在极限情况下的解与已知的解一致：

1. 当gamma;=0时，解与核-壳颗粒的解一致[55]：

2.假设beta;=alpha;,a=0，可以得到关于在颗粒-液体界面热跳跃颗粒的解[36]：

为了描述基于中空纳米颗粒的纳米流体的导热系数，假设alpha;=0并得到了最终的关系式：

4、结果

测量结果如图4。对基于水、乙二醇和异丙醇三种基础液体的纳米流体进行了测量。对于水和异丙醇，测量到纳米颗粒的体积含量为1.5 %；对于乙烯甘醇溶液测得的纳米颗粒含量高达2.2 %。这是因为破坏了前两种流体的稳定性，纳米颗粒的体积含量进一步增加。对于不同的基本流体，不同的测量误差值也显示了这种现象。尽管每个点都是通过平均50次以上的测量获得的，但这些值还是存在着明显的分散性。注意到基于乙二醇的纳米流体是最稳定的；同时，测量误差最小。

图4.相对热导率与纳米颗粒体积分数的关系

麦克斯韦理论关于纳米粒子低体积含量的相关性计算也在图4中；符合这些实验的条件。观察到水基纳米流体的最大数据散射。考虑到统计处理，这种分散会产生0.3 %的误差。在图中，它仅显示了水基纳米流体。当前研究的主要结果表明，所有实验数据都明显低于理论相关性。对于基于乙二醇、异丙醇和水的纳米流体，热导率的增加与纳米颗粒体积分数之间的比例系数(与麦克斯韦理论相比)分别为0.37、0.27和0.17。以下章节对可能的原因进行分析。

5、讨论

实验值低于理论预测有三个可能的原因。第一，在实验中，使用了中空颗粒，这自然减少了颗粒内部的热流，并影响了纳米流体的热导率。第二，纳米颗粒材料是gamma;- Al₂O₃。这种修改仅在纳米尺寸范围[63]内是稳定的。可以认为gamma;-Al₂O₃的导热率低于已知的导热率良好的alpha;-Al₂O₃的导热率。第三，在实验中使用了半径小于5 nm的纳米粒子，并且粒子边界处的温度跳跃可能产生显著的影响。

对于下面的分析，提出几点修正。根据公式(2)，C_f/b³值表征的是纳米颗粒比体积含量热导率的增加。对于当前实验的条件(phi;lt;lt;1)，公式(2)可以改写为:

根据公式(3)，值(-C_f/b³)可以在-1到0.5之间变化。特别地，值(-C_f/b³)=1对应于当纳米颗粒材料的热导率高于流体的热导率时的情况，并且没有考虑颗粒边界处的温度跳跃。对于导热不良的纳米颗粒或高卡皮查跳跃的另一个极限情况，纳米流体的热导率与基本流体热导率相比的降低关系为K_nf/K_f=1-3/2phi;。

从理论上分析，空腔对没有界面热阻的纳米流体导热率的影响(gamma;=0，公式(7))。(-C_f/b³)与颗粒和流体的导热率之比的关系beta;=K_s/K_f为图5中所示的三个值(a/b)³: (a/b)³=0对应于固体颗粒；(a/b)³= 0.16对应于当前实验的条件；(a/b)³= 0.5对应于颗粒，其空腔半径约为颗粒半径的0.8。如果使用alpha;-Al2O3导热系数的表格值，beta;=K_s/K_f，水、异丙醇和乙二醇分别约为70、100和150。根据图5，随着beta;的增加和减少，空腔的作用变得更小。对于较高的beta;值，这种效应显然与颗粒材料的高热传导率和对半径比(a/b)的较高(立方)依赖性有关。根据图5，就像实验中观察到的那样，即使(a/b)=0.8((a/b)³=0.5)的比率也不会对纳米流体的热导率产生如此强的影响。

图5.系数(-C_f/b³)与beta;=K_s/K_f的相关性

上述分析表明允许忽略空腔对实验中观察到的效果的影响。通过对粒子导热率和温度的变化边界效果的分析，(C_f/b³)对参数gamma;=GK_f/b的关系如图6所示，对于在(a/b)³=0.16：beta;=infin;中的三个beta;值是纳米颗粒材料的无限导热率的情况；beta;=66对应于alpha;-Al₂O₃和水的导热率之比。

beta;=30的曲线用来解释beta;对纳米颗粒较低热导率的影响。该图显示纳米颗粒材料的热导率，甚至比alpha;-Al₂O₃热导率的低两倍

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[608570]，资料为PDF文档或Word文档，PDF文档可免费转换为Word