用小波作为输入支持向量机和神经网络的磁共振脑图像分类外文翻译资料

英语原文共 7 页，剩余内容已隐藏，支付完成后下载完整资料

生物医学信号处理与控制1（2006）86-92

www.elsevier.com/locate/bsp

用小波作为输入支持向量机和神经网络的磁共振脑图像分类

Sandeep Chaplot a，L.M。Patnaik a，*，N.R。 Jagannathan b

计算神经生物学组，印度科学研究院超级计算机教育与研究中心，印度班加罗尔560012

b全印度医学科学院核磁共振系，Ansari Nagar，印度新德里110029

2006年2月17日收到; 2006年5月8日收到修订后的表格; 2006年5月11日接受

摘要

在本文中，我们提出了一种新的方法，使用小波作为神经网络自组织映射的输入和支持向量机的人脑磁共振（MR）图像的分类。所提出的方法将MR脑图像分类为正常或异常。我们使用52个MR脑图像的数据集测试了所提出的方法。使用神经网络自组织图（SOM）和98％来自支持向量机，实现了超过94％的良好分类百分比。我们观察到，与基于自组织映射的方法相比，支持向量机分类器的分类率很高。

＃2006 Elsevier Ltd.保留所有权利。

关键词：磁共振成像（MRI）;离散小波变换（DWT）;人工神经网络（ANN）;自组织地图（SOM）;支持向量机（SVM）

1. 介绍

磁共振（MR）成像被引入临床医学，并且从那时起就在脑成像中扮演了无与伦比的重要角色。磁共振成像是一种先进的医学成像技术，已被证明是研究人类大脑的有效工具。 MR图像提供的关于软组织解剖结构的丰富信息极大地改善了脑病理诊断和治疗的质量。然而，数据量对于手动解释来说太多了，因此非常需要自动图像分析工具。 MR成像最重要的优点是它是一种非侵入性技术。与其他成像模式相比，可以看到的细节水平非同寻常。 MR成像提供身体内器官和结构的二维和三维图像。

*通讯作者：CEDT建筑微处理器应用实验室，印度理工学院239室，班加罗尔，印度卡纳塔克邦，560012。电话： 91 80 23600451;传真： 91 80 2360683。

电子邮件地址：lalit@micro.iisc.ernet.in（L.M。Patnaik）。

1746-8094 / $ - 见前面的＃2006 Elsevier Ltd.版权所有。 DOI：10.1016 / j.bspc.2006.05.002

从MR脑图像中提取基本特征对于正确分析这些图像是必不可少的。独立分量分析（ICA）[1]，傅立叶变换[2]和小波变换[3]是用于从图像中提取特征的几种方法。虽然小波是一种相对较新的结构，但它已成为工程师，物理学家和数学家进行时空频率分析的首选工具。与仅提供信号频率分析的傅立叶变换不同，小波变换提供时频分析，这对于模式识别特别有用。

我们使用机器学习算法来获得正常或异常两类图像的分类。

人工神经网络（ANNs）[4,5]具有生物学启发。它们由许多并行操作的非线性计算元件组成，并且以类似于生物神经网络的模式排列。人工神经网络根据他们的环境修改他们的行为，从经验中学习，并从之前的例子推广到新的例子。人工神经网络已成为大类模式识别任务的首选技术。 Lippmann [6]对人工神经网络进行了很好的评论。自组织映射（SOM）是一种无监督算法，它具有优于其他网络的优点，可以自动形成相似图，并可以产生抽象。

自组织映射可以推广到非矢量符号数据，而其他网络则不是[7]。

支持向量机（SVM）是一种机器学习技术，源于统计理论[8]，用于图像分类。主要优点是它能够模拟高度非线性系统，决策表面的特殊属性确保了非常好的通用性。由于其计算效率和良好的泛化性能，SVM已广泛用于模式识别应用。

因此，ANN和SVM在识别和分类任务中非常有吸引力。比较两种方法的结果。

本文的其余部分安排如下。第2节介绍了图像的输入数据集和特征提取方法以及分类的简短描述。第3节包含结果和讨论，而结论在第4节中给出。

1. 材料和方法
   1. 输入数据集

输入数据集由轴向，T2加权，256times;256像素MR脑

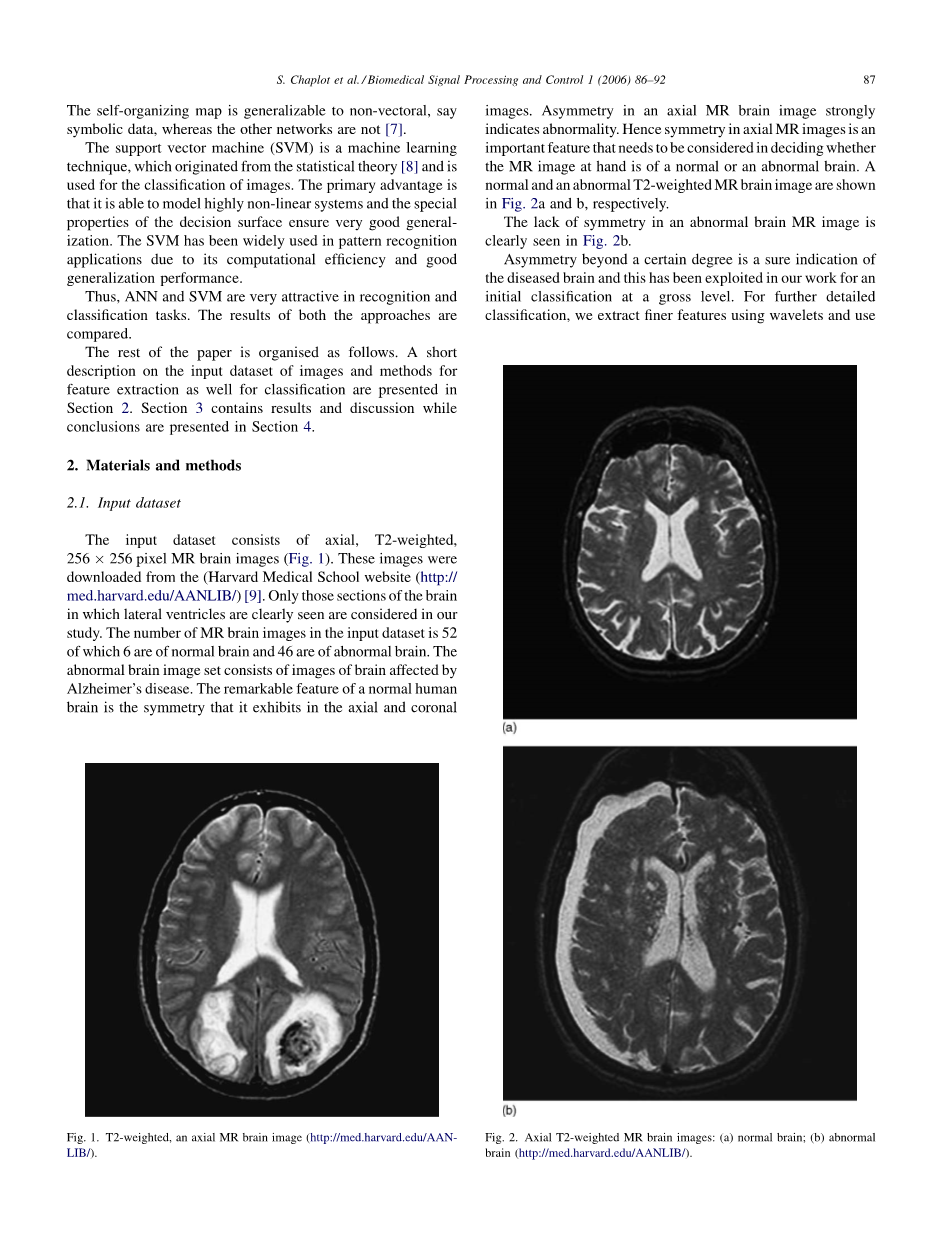
图像组成（图1）。这些图像是从（哈佛医学院网站（http：// med.harvard.edu/AANLIB/）[9]下载。在我们的研究中，只考虑了能够清楚地看到侧脑室的大脑部分.MR脑部的数量输入数据集中的图像中有52个，其中6个是正常脑，46个是异常脑。异常脑图像集由受阿尔茨海默病影响的大脑图像组成。正常人脑的显着特征是它呈现的对称性在轴向和冠状

图1.T2加权，轴向MR脑图像（http://med.harvard.edu/AAN-LIB/）。

图片。轴向MR脑图像中的不对称性强烈表明异常。因此，轴向MR图像中的对称性是在决定手边的MR图像是正常脑还是异常脑时需要考虑的重要特征。正常和异常的T2加权MR脑图像分别如图2a和b所示。

在图b中清楚地看到异常脑MR图像中缺乏对称性。

超过一定程度的不对称性是患病大脑的确定指示，并且这已经在我们的工作中用于初级分类。为了进一步详细分类，我们使用小波和使用提取更精细的特征

图2.轴向T2加权MR脑图像：（a）正常脑; （b）大脑异常（http://med.harvard.edu/AANLIB/）。

88S。

这些功能用于自组织神经网络和支持向量机分类。

• 1. 基于小波的特征提取

小波是数学函数，它将数据分解为不同的频率分量，然后以与其比例相匹配的分辨率研究每个分量。小波已成为分析复杂数据集的强大新数学工具。傅立叶变换仅基于其频率内容提供图像的表示。因此，当小波函数在空间中定位时，该表示不是空间定位的。傅里叶变换将信号分解为频谱，而小波分析将信号分解为范围从粗糙度范围的等级。因此，小波变换[3]提供了各种分辨率的图像表示，是从图像中提取特征的更好工具。

• • 1. 离散小波变换（DWT）

DWT是小波变换的实现，使用离散的小波尺度集并且遵循一些定义的规则进行平移。对于实际计算，有必要对小波变换进行离散化。比例参数在对数网格上离散化。然后，相对于比例参数离散化平移参数（t），即在二元（对数的基数通常选择为两个）采样网格上进行采样。离散化的比例和平移参数由下式给出，

s = 2 m且t = n2 m，其中m，n 2 Z，所有整数的集合。小波变换将信号x（t）分解成一系列合成小波，如下面的等式1中给出的。 （2）和（3），

对于离散时间信号x [n]，I八度音阶上的小波分解由下式给出

其中ci，k i = 1 I：小波系数和di，k i = 1 I：缩放系数。

小波和缩放系数由下式给出，

其中gi [n 2ik]和hI [n 2Ik]分别代表离散波导和缩放序列，（*）表示复共轭。

• • 1. DWT在两个方面

在图像的情况下，DWT分别应用于每个维度。这导致图像Y被分解成第一级近似分量Y 1，并且是详细的

个

因此，小波函数族表示在

组分Y 1，Y 1

和Y1;对应水平，

HOD

（1），

（1）

垂直和对角线细节[10]。图3描绘了该过程

将图像分解为近似和详细的组件。近似分量（Ya）包含图像的低频分量，而详细分量（Yh，Yv

图3.图像Y的小波变换直到第二级。 Y1和Y2分别是第一和第二级近似分量。 Y1，Y1和Y1是第一级

细节组件。 Y2，Y2和Y2是二级细节组件。

HOD

和Yd）包含高频成分。从而，

如果将DWT应用于Y 1，则获得第二级近似和详细分量。类似地执行更高级别的分解。如果该过程重复多达N个级别，则可以根据第N个近似分量（YN）和下面在等式1中给出的所有详细分量来写入图像Y. （8），

一个

一个

在每个分解级别，分解信号的长度是前一级信号长度的一半。因此，获得的近似分量的大小

Ntimes;N图像的第一级分解为N / 2times;N / 2，第二级为N /

4times;N / 4，依此类推。作为水平

增加了分解，获得了紧凑但较粗略的图像近似。因此，小波为解释图像信息提供了一个简单的分层框架[11]。

• • 1. 母小波的选择

压缩或局部化的小波变换的基础被称为小波变换的母小波。在大脑的MR图像的情况下，像素强度值平滑地变化，这不能通过Haar小波非常有效地表示[12]。 Daubechies-4（DAUB4）[13]小波虽然计算成本昂贵，但与Haar小波相比，具有更好的分辨率，可以平滑地改变信号。因此，我们选择了Daubechies-4小波，这提供了出色的分类精度。在本文中，我们提取了MR脑图像的DAUB4小波逼近系数，并将它们用作特征向量进行分类。

• 1. 自组织地图（SOM）

Kohonen等人。 [7]提出了一种称为自组织映射的无监督方法。 SOM [14]是一种用于分析和可视化高维数据的强大神经网络方法。它将高维测量数据之间的非线性统计关系映射到简单的几何关系，通常在二维网格上。 SOM是一种无监督的方法，我们只提供一系列输入模式，它自己学习如何将这些模式组合在一起，以便类似的模式产生类似的输出。

SOM的第一部分是数据。自组织地图的想法是将n维数据投影到可以在视觉上更好理解的东西。 SOM的第二个组成部分是权重向量。

输入数据点映射到二维网格上的SOM单元。通过简单的随机学习过程从训练数据样本中学习映射，其中SOM单元相对于从数据中提取的特征向量以小步长调整并且一个接一个地呈现（以随机顺序）。

SOM组织自己的方式是竞争样本的代表。通过学习变得更像样本以期赢得下一次比赛，神经元也被允许改变自己。正是这种选择和学习过程使权重组织成一个代表相似性的地图。

构建SOM的第一步是初始化权重向量，从那时起我们随机选择一个样本向量并搜索权向量的映射以找出最能代表该样本的权重向量。由于每个权重向量都有一个位置，因此它也具有靠近它的相邻权重。算法的步骤如下：

步骤1.初始化权重 - 初始化每个权重它们被初始化为0到0.5之间的随机数。

步骤2.获得最佳匹配单元 - 呈现输入模式计算从每个权重到所选样本向量的距离x，并确定获胜权重或最佳匹配单位c，使得

如果有的话，最短距离的体重是胜利者在具有相同距离的多于一个重量的情况下，在具有最短距离的权重中随机选择获胜权重。

步骤3.缩放邻居 - 调整最佳匹配单元c和所有邻居单元

的权重;其中i是邻居权重的索引，t是整数，离散时间坐标。邻域内核hci（t）是时间函数和相邻权重i与获胜权重c之间的距离; hci（t）定义输入模式对S

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[18195]，资料为PDF文档或Word文档，PDF文档可免费转换为Word