使用CFD提高离心泵性能的设计技术外文翻译资料

英语原文共 11 页，剩余内容已隐藏，支付完成后下载完整资料

使用CFD提高离心泵性能的设计技术

摘要

离心泵是工业领域最常用的泵。设计一个更高性能的泵，需要使用机械概念进行设计优化。在本研究中，对叶轮和蜗壳进行了优化，以提高离心泵的性能。采用流体机械设计理论和内部设计数据库进行基础叶轮设计，并通过数值分析评估其性能。然后进行设计优化，以提高基础叶轮的性能。叶轮的设计变量和变量范围已被定义。基于这些设计变量和范围，生成实验组，并通过数值分析评估其性能。然后根据响应面法（RSM）分析，以产生满足设计规范的优化叶轮。最后，优化叶轮的性能通过数值分析验证。Stepanoff理论也被应用在蜗壳的设计中，并通过修改蜗壳截面分布和性能评估得到了适当的设计，进行数值分析。

关键词：离心泵;叶轮;设计优化;响应面法；蜗壳；Stepanoff理论；截面分布;计算流体力学（CFD）

1.介绍

泵是一种典型的将机械能转化为流体压力和动能的流体机械。通过泵的形状和性能特点，可以分为各种类型（例如：离心泵，混流泵，轴流泵）。和其他类型泵相比，离心泵提供高性能压力[1]。但是，他们处理工作流体的能力相对较低[2]。离心泵长期应用于许多工业领域，如水，污水，排水，和化工行业。已经进行了许多研究来改进离心泵，包括其性能[3-7]。因此，最近的离心泵显示出来高性能水平。然而，需要更系统的方法，如优化技术来实现更显著的性能提升。在泵的所有部件中，因为流体通过叶轮在泵中流动时产生能量，所以叶轮在离心泵性能上具有最大影响。因此，许多研究专注于叶轮的优化来提高离心泵性能[8-10]。提高叶轮的性能需要基于变量评估的设计优化。

除叶轮外，蜗壳是影响离心泵性能的另一主要部件。 蜗壳从泵中获得流体并将其输送到管道。产生内部流量时的动态压力损失可能会降低泵的性能。因此，需要设计蜗壳以尽量减少压力损失。Stepanoff理论已被应用于蜗壳的设计中来控制横截面分布[11]。 然而，由斯塔潘夫理论计算出的横截面分布并不与所有类型的蜗壳兼容。 因此，需要验证计算的横截面分布来设计优化蜗壳[12,13]。

在本研究中，研究了满足设计规格的离心泵的最佳设计。基础叶轮采用流体机械设计理论和内部设计数据库设计。通过数值分析评估基础叶轮的性能。为了提高基础叶轮的性能，进行了设计优化。定义叶轮的设计变量和可变范围。 基于这些设计变量和范围，生成实验组，并通过数值分析评估其性能。 然后根据响应面法（RSM）分析产生满足设计规格的优化叶轮。 最后，通过数值分析验证了优化叶轮的性能。 Stepanoff理论应用于蜗壳的设计中。 通过数值分析修改蜗壳的横截面分布和性能评估，提出了适当的设计。

2.选择基础叶轮

2.1基础叶轮的设计

本研究的设计规范如表1所示。为了进行研究，基础叶轮设计符合设计规范。

叶轮的3D几何形状可以通过子午平面的设计和叶片的角度来产生。如图1（a）所示，将包含叶片上的几何信息的子午平面投影到2D平面上，其中包含叶片上的基本信息。 为了确定子午平面，需要关于比转速（Ns）的信息。比转速由流体机械理论定义如下：

(1)

其中N、Q和H分别表示泵的转速，流量和扬程。根据比转速选择泵的类型和子午面的形状。 本研究中泵的比转速约为240.基础叶轮的子午平面是依据比转速建立的内部设计数据库设计的[14]。基础叶轮的子午平面设计信息如表2所示。

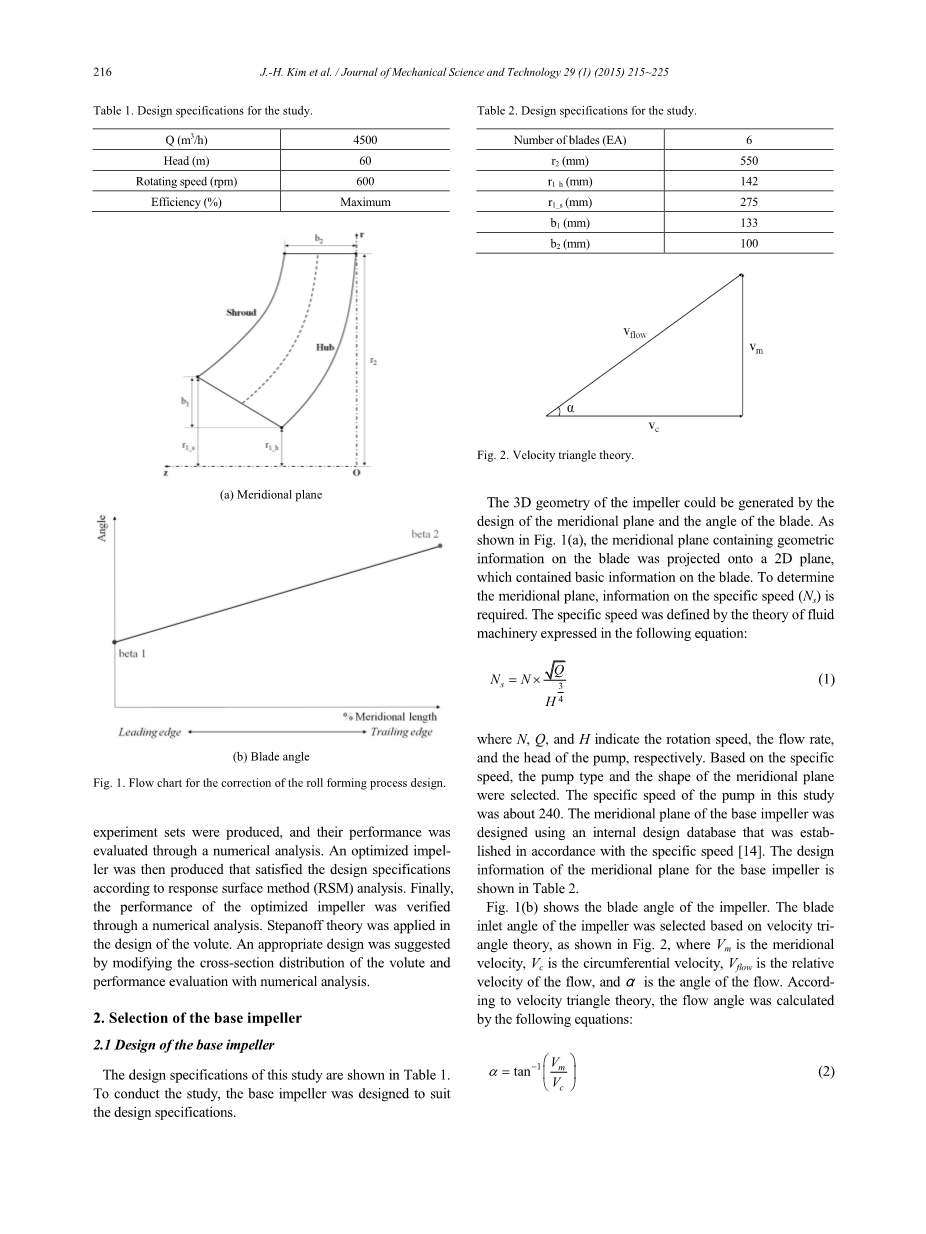
图1（b）表示叶轮的叶片角度。 叶片入口角度根据速度三角理论选择，如图2所示，其中Vm是子午速度，Vc是圆周速度，Vflow是流动的相对速度，alpha;是流动角度。 根据速度三角理论，流角由下式计算：

(2)

(3)

(4)

其中A表示流体的横截面积，omega;表示角速度，r表示叶轮半径。为了设计基础叶轮的入口角，使用速度三角理论计算流动角度。 计算的流动角度在下盖板处为37°，在上盖板处为21°。 上盖板和下盖板的流角被选择为基础叶轮的入口角(beta 1_h andbeta 1_s)。 基础叶轮的出口角度(beta 2_h and beta 2_s)，通过扬程设计规格的水平确定，并且上盖板和下盖板的流角均为24°。

2.2使用CFD评估基础叶轮的性能

如图3所示。使用ANSYS BladeGEN ver 13生成基础叶轮的3D几何模型。数值分析所使用的流体计算域是如图4所示的3D几何模型。当流体计算域产生时，使用周期条件选择一个叶轮叶片的流道，并且考虑到数值分析的时间。对于流体计算域，使用ANSYS TurboGrid ver生成结构化网格。进行叶轮的网格依赖性测试，选择可靠的网格进行性能评估。在不同数量的网格节点下，使用扬程和效率结果进行叶轮的网格依赖性测试。当流量为4500 m3 / h。尽管网格节点数量发生变化，但每个部分的比例保持不变。基于叶轮的网格依赖性测试结果，如图5所示。最终选择了具有0.1％或更低性能误差范围的网格系统。所选网格的总节点数量约为20万，叶片部分约为15万。该网格系统的平均y 值为1.7，小于2。对叶轮进行数值分析时，采用采用基于k-omega;模型的SST模型,一个湍流模型。使用SST模型进行数值分析，

应用Low-Reynolds模型计算y 值小于2的近壁面流动。使用壁面函数计算的可靠性高于k-omega;模型[15]。所选择的网格系统如图4所示。

为了评估叶轮的性能，使用商业3D粘性流体分析应用ANSYS CFX ver进行数值分析。为了检查流场的特性，采用了不可压缩湍流分析的3D平均Navier-Stokes方程[16]。 数值分析的控制方程通过有限体积法（FVM）进行离散化，使用二阶或更高精度的高分辨率技术进行离散化[17,18]。 对于数值分析的边界条件，参考压力设定为1个标准大气压，并且将入口处的压力设置为0个大气压，使得入口处为大气压状态，与此同时出口处设置为流量出口。 将转子（N）的转数设定为600 rpm，工作流体为清水。在周期条件下，对一个流道进行数值分析。

从CFD的计算结果可以确定基础叶轮的性能，如图6所示。 扬程为65米，额定工况（Q：4500立方米/小时）下的效率为97.1％根据数值分析的结果可知，基础叶轮的性能满足设计规范。 然而，评估性能排不包括蜗壳和其他部件损失。 通过先前的研究验证了选择设计边际的损失和误差[19]。
考虑到这些损失和数值分析的误差（约12％），基础叶轮似乎不符合设计规范。 此外，最高效率点为4950 m3 / h，与设计规格（Q / Qdesign = 1.1）不同。 因此，基础叶轮需要进行修改。

3.叶轮优化

为了设计满足研究设计规范的离心泵，进行了RSM和数值分析的优化过程。优化过程如下表所示，如图7所示。

3.1叶轮的设计变量

建立叶轮优化设计变量。 由于设计的局限性，子午平面的变量被固定在基本模型值中。 对于叶片角度，使用四个设计变量：叶轮后盖板的入口角（beta;1_h），叶轮前盖板的入口角（beta;1_s），叶轮后盖板的出口角（beta;2_h）和叶轮前盖板的出口角（beta;2_s）。 所选设计变量和范围如表3所示

3.2叶轮优化方法

使用RSM和数值分析优化叶轮。 由Box和Wilson于1951年推出的RSM，是一种众所周知的估计独立变量之间的相互作用效应的方法，而不是对每个独立变量的每个级别进行阶乘设计实验[20]。 在RSM中，至少有两种以上的变量是目标，优化算法使用自变量的变异性来估计响应函数之间的函数关系。有几种类型的RSM。 当响应面的估计是初级时，使用两级因子设计，当响应面的估计是次要的时，采用三级因子设计。.

使用RSM进行优化，共生成了25个实验组用于数值分析，以适应中心组合。 最初，共采用30个实验组进行优化，采用RSM的中心组合。 然而，考虑到数值分析的特征，消除了用于确认重复性能评估的误差，这些组中的五个。 生成的实验组的变量值如表4所示。所有实验组同时采用与基础叶轮相同的数值分析进行性能评估。

3.3生成优化叶轮

基于每个实验组的性能评估结果，使用MiniTab程序优化叶轮进行RSM分析。图8显示了从RSM获得的设计优化结果。考虑到数值分析的损失和误差范围，设定了满足设计规范的目标性能。目标性能将扬程设置为69，与此同时离心泵效率最高。优化分析预测，当beta 1_h为35°、beta 1_s为19°、beta 2_h为28°和beta 2_s为28°时，扬程为69米，效率为69.3％，通过使用RSM优化，生成优化叶轮，如图9所示，使用数值分析评价其性能。结果如图10所示。结果显示，额定工况（Q：4500 m3 / h）下的扬程为69.1m，效率为98.3％，与估计结果一致。扬程高出4.1米，效率比基础叶轮提高了1.2％。考虑到损耗和误差范围，优化叶轮的性能被认为满足于设计规范。除此之外，叶轮优化解决了基础叶轮的最大效率点和额定工况点之间的不匹配问题。

3.4内部流场比较

为了研究基础叶轮和优化叶轮性能差异的原因，根据数值分析结果对内部流场进行了分析。 图11显示了额定工况点（Q：4500m 3 / h）下，基础叶轮和优化叶轮的叶片部分的子午平面上的压力云图。 在基础叶轮的情况下，前盖板和后盖板的压力升高程度不同。 该偏压的压力上升导致不均匀的流动并且导致性能的降低。 另一方面，优化叶轮在前盖板和后盖板侧显示压力均匀的升高。

图12显示基础叶轮和优化叶轮在额定工况点（Q：4500m 3 / h）下的流线分布。从图中可以看出，在基础叶轮中部产生涡流区，而优化叶轮则抑制了流动分离。 基础叶轮在后盖板上具有较高的压力上升，如图11所示。 由于压力分布，验证了前盖板上的内部流速比在后盖板上的速度更快。 由于跨度位置的速度差，在基础叶轮上发生流动分离，而优化叶轮上因为具有一致的压力分布，所以流动分离被抑制。
不均匀流动的改进提高了叶轮的性能。 基于这些结果，选择优化叶轮用于最终设计。

4.选择基础蜗壳
4.1设计基础蜗壳

蜗壳是收集流体并连接到螺旋管的装置。 由于它具有易于制造的简单形状，因此已广泛用于离心泵。在设计泵中蜗壳的横截面分布时，主要使用Stepanoff理论。横截面分布随着角度成比例地变化，以在蜗壳中保持恒定的流速。 根据Stepanoff理论，蜗壳中的流速定义如下：

(5)

其中g表示重力加速度，H表示扬程，K表示实验常数。 K由比转速定义如下：

(6)

蜗壳根据旋转角度的横截面分布可以从伯努利方程定义如下：

(7)

为了进行研究，通过Stepanoff理论设计了适合优化叶轮的基础蜗壳。 基础蜗壳中的流速为14 m/s，计算出与角度相对应的各个横截面分布。 基础蜗壳的横截面形状如图13所示。 蜗壳（b3）入口的径向角（theta;）和宽度分别在所有旋转角度固定为15°和175 mm。 蜗壳（R）的高度（h）和圆周半径，随着旋转角度的横截面分布而改变。

4.2 使用CFD对基础蜗壳进行性能评估

基于计算出的横截面分布和基础蜗壳的横截面形状，使用SolidWorks 2013生成了基础蜗壳的流体域，如图13所示。生成的流体域被用作基础蜗壳的计算域。使用ANSYS ICEM CFD ver.13生成用于计算域的非结构化网格系统。进行蜗壳的网格依赖测试以选择可靠的网格进行性能评估。蜗壳的网格依赖性测试使用了不同数量的蜗壳的网格节点的扬程和效率结果，如在叶轮的网格依赖性测试中所做的那样。当进行蜗壳的网格依赖试验时，应用优化叶轮。合格的叶轮网格系统通过叶轮的网格依赖性测试，2.2.1用于叶轮网格系统的优化。为了与蜗壳结合，优化叶轮的计算域使用整个流体域。图14显示出网格依赖性测试的结果。基础蜗壳的选定网格系统如图15所示。有250万个节点。所选蜗壳的网格系统的平均y 值约为15。因此，在使用该蜗壳网格系统的情况下，应用壁面函数计算靠近墙壁的流体[15]。

由350万个节点组成的网格系统，需要小于2的y 值来计算使用Low-Reynolds模型的壁面附近的流体。 然而，350万个节点的网格系统的结果与通过网格依赖测试所示的具有250万个节点的网格系统的结果相似。 结果，由于分析效率如存储空间和分析时间，使用了250万个节点的网格。

为了评估带有蜗壳的叶性能，使用商业3D粘性流体分析软件ANSYS CFX ver. 13进行了数值分析。主要的数值分析方案与叶轮的数值分析相同。大多数进行数值分析的边界条件也设定了叶轮的情况。然而，叶轮的整个计算域用于调节叶轮出口和蜗壳入口的界面面积比，而不是周期性条件。此外，在叶轮和蜗壳的交界面，应用阶段平均状态。当应用阶段平均状态时，平均值上的数据作为旋转域旋转时每个接口点的数据共享[21]。因此，根据旋转位置的性能没有差别。因此，阶段平均状态通常用于流体机械的性能评估[22-26]。

从

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[138886]，资料为PDF文档或Word文档，PDF文档可免费转换为Word