磁热影响和磁制冷外文翻译资料

英语原文共 13 页，剩余内容已隐藏，支付完成后下载完整资料

磁热影响和磁制冷

Ames实验室和材料科学与工程系，爱荷华州立大学，255 Spedding，Ames，IA 50011-3020，美国于1999年1月21日收到；1999年4月9日修订表格收到

摘要：讨论了磁热效应的现象以及最近的进展和未来的需要，在新的磁性制冷剂材料的磁热性质方面的表征和探索。 此外，还回顾了磁性冰箱设计的最新进展。 （1999 Elsevier Science B.V.保留所有权利）

关键词：磁热影响；磁制冷；稀土材料；铁磁体；顺磁体退磁；绝热退磁

1. 磁热影响
   1. 发现和基础

磁热影响（MCE），或绝热温度变化(Delta;Tad),，这是检测由于磁性材料的磁场变化引起的加热或冷却，最初是由沃伯格在铁的发现的。MCE的本质是解释和达到一个过程，称为绝热退磁，是由德拜和吉奥克独立提出的。

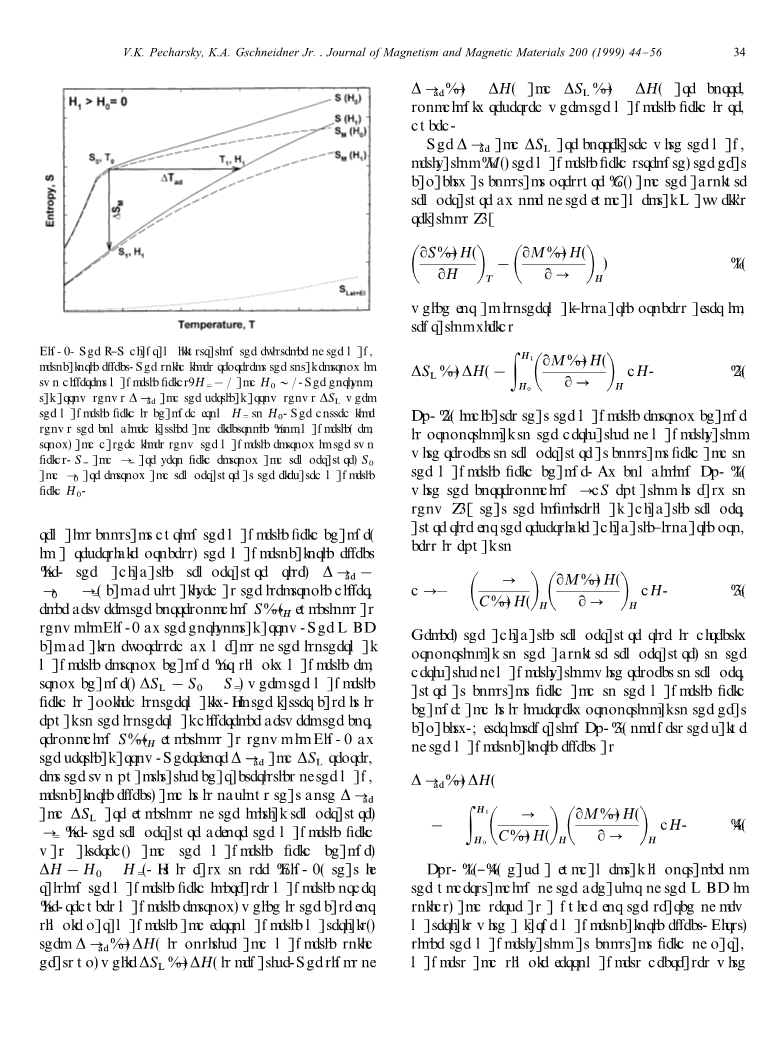
MCE是所有磁性材料固有的、是因与磁场磁晶格的耦合，从而改变固体的磁性部分的熵，就像一个气体压缩，等温磁化的顺磁性或软磁体减少熵，在一个可逆过程，退磁（这是一个类似于气体的膨胀）恢复零场磁熵系统。在附近的一个铁磁体的磁有序温度MCE的热力学（居里温度，Tc）是在图1的示意性地示出。在恒定压力下的磁性固体的熵S（T，H），这是一个双方的磁场强度的函数（H）和绝对温度（T），是磁性的，S_M，晶格的总和，S_Lat、电子、S_EI贡献：

S(T,H)=S_M(T,H) S_Lat(T) S_EI(T) (1)

其表示出了在两个恒定磁场（零磁场H0和非零磁场，H1）中的铁磁材料以及相应的磁和非磁项。 当绝热地施加磁场时（即当系统的总熵为时）。

图1.表示出了磁热效应存在的S-T图。 实线表示两个不同磁场中的总熵：H0=0和H1gt;0。 当磁场从H0变为H1时，水平箭头显示Delta;Tad，垂直箭头显示Delta;SM，虚线表示组合的晶格和电子（非磁性）熵，虚线表示磁熵 在两个S0和T0是零“熵和温度，S1和T1是在升高的磁场H1处的熵和温度

在磁场变化期间保持恒定，在可逆过程中，磁热效应（即绝热温度升高）可以被可视化为如图所示的相应的S（T）H函数之间的等熵差在图1中由水平箭头表示。当等温施加磁场时，MCE也可以通过等温磁熵变（或简单地磁熵变）表示。在后一种情况下，它等于相应的S（T）H函数之间的等温差，如图3所示。 1由垂直箭头。因此Delta;Tad和Delta;SM代表磁热效应的两个定量特性，很明显，Delta;Tad和Delta;SM都是初始温度的函数，即T0（即磁场改变前的温度） （图1），如果提高磁场增加磁顺序（即降低磁熵，这是简单的顺磁性和铁磁性材料的情况），这是容易看到的（图1） ），则Delta;Tad（T，Delta;H）是正的磁性固体加热，而Delta;SM（T，Delta;H）是负的。Delta;Tad（T，-Delta;H）和Delta;SM（T，-Delta;H）在磁场减小时相应地反转。

Delta;Tad和Delta;SM与磁化强度（M），磁场强度，恒定压力下的热容量（C）和绝对温度之间有一个基本的麦克斯韦关系

其对于等温等压过程的积分产率

式（3）表示磁熵变与磁场相对于恒定磁场的温度和磁场变化的导数成比例。 通过组合方程 （2）与相应的T dS方程，很容易显示[4]可逆绝热等压过程的无穷小绝热温升等于

因此，绝热温度升高与绝对温度成正比，与磁场相对于恒定磁场和磁场变化的温度的导数成正比; 它与热容量成反比。积分方程（4）将磁热效应的值作为

式（2）-（5）对于理解固体中MCE的行为具有根本的重要性，并且用作具有大磁热效应的新材料的搜索的指南。首先，由于顺磁体和简单铁磁体的恒定磁场的磁化随着温度的增加而降低[即（M / T）Hlt;0）]，则Delta;SM（T）Delta;H应为负的，Delta;Tad（T）Delta;H为正的（方程式（2）（M / T）H）中，Tc是最大的（式（4）和（5）），这与图1一致。第三，虽然从方程（4）和（5）不能直接得出，因为在常数“C”下的热容量，接近Tc的场合也是异常的，在Delta;H →0时的居里温度下，在铁磁体尖峰中已经表明Delta;Tad（T）Delta;H, Delta;SM（T）Delta;H的行为应该类似。第四，对于相同的Delta;Tad（T）Delta;H, Delta;SM（T）Delta;H的行为，即它将在低于和高于1℃时逐渐降低。在较高的绝对温度下，以及当固体的总热容较低时（方程（5）），较大的值将是较大的。后一点对于理解这样的事实是至关重要的，即顺磁体显示（Delta;H）仅在接近绝对零度的温度，其中（M / T）H的限制值容易通过可忽略的晶格热容设定。此外，在高温下，只有当固体自发地命令时，即（M / T）H的值变得显着时，才预期可测量的绝热加热（或冷却）。

• 1. 磁热探测的测量

磁热效应可以直接测量或者可以从测量的热容的磁化或场依赖性间接计算。直接技术总是涉及在磁场H0和HF中测量样品温度（T₀和T_F），其中下标0和F分别表示初始和最终磁场。 然后将Delta;Tad（T）Delta;H为给定的T₀和Delta;H =H_F-H₀的T_F和T₀之间的差。

直接MCE测量可以使用接触（即当温度传感器与样品直接热接触时）和非接触技术（即当样品温度在没有传感器直接连接到样品的情况下测量时）同时进行。由于在直接MCE测量期间需要磁场的快速变化，所以当通过对磁体充电/放电或通过将样品移入和移出磁场来提供磁场变化时，可以在固定的样品上进行测量均匀磁场体积。使用固定化样品和脉冲磁场，直接在1到40T的磁场中进行MCE测量。电磁体的使用通常将磁场强度限制为小于2T。实验装置（其中样品或磁体被移动以提供变化的磁场环境）通常采用超导或永磁体，其将磁场范围限制为0.1-10T。直接实验技术的精度取决于温度测量中的误差，场设置中的误差，样品的热绝缘的质量（当MCE大时，这成为关键的误差源，因此破坏绝热条件） ，补偿方案消除了变化磁场对温度传感器读数的影响。考虑所有这些影响，测量精度在5-10％范围。

与仅产生绝热温度变化的直接MCE测量不同，间接实验允许计算Delta;Tad（T）Delta;H和Delta;SM（T）Delta;H热容量测量值，或只是Delta;SM（T）Delta;H磁化测量。作为温度和磁场的函数的实验测量的磁化在方程（3）的数值积分之后提供Delta;SM（T）Delta;H，并且被合理地建议作为用于快速筛选预期磁性制冷剂材料的有用技术。从磁化数据计算的Delta;SM（T）Delta;H的精度取决于磁矩，温度和磁场测量的精度。由于涉及数值积分，并且由于分别用测量的Delta;M，Delta;T和Delta;H代替精确的微分（dM，dT和dH），所以来自磁化的Delta;SM（T）Delta;H的典型精度测量报告在3-10％的范围内。特别是对于小的Delta;SM（T）Delta;H值，相对误差可能变得明显更大。

在恒定磁场C（T）H中作为温度的函数测量的热容量提供了磁性材料相对于其磁热效应的完全表征，因为磁性固体的熵可以从热容量积分

其中S0和S0，H是零温度熵。 在浓缩系统中，这些是相同的（即S₀=S_0，H），因此，Delta;Tad（T）Delta;H和Delta;SM（T）Delta;H的计算是直接的使用热容量数据的MCE计算的精度在很大程度上取决于热容量测量和数据处理（公式（6））的精度，因为Delta;Tad（T）Delta;H和Delta;SM（T）Delta;H是两个大量（温度和总熵）之间的微小差异，热容量误差Delta;SM（T）Delta;H给出

其中S（T）H=0和sigma;S（T）Hne;0分别是零磁场熵和非零磁场熵的误差。 Delta;Tad（T）Delta;H中的误差也与熵的误差成正比，但它与熵相对于温度的导数成反比

应当注意， （7）和（8）产生计算的磁热效应的绝对不确定性，因此，对于小的MCE值，相对误差显着增加（图2和图3）。 因此，假设热容量测量的精度是磁场无关的，对于较大的Delta;H，Delta;Tad（T）Delta;H和Delta;SM（T）Delta;H的相对误差将减小。

• 1. 顺磁性的磁热效应

如上所述，顺磁性的MCE仅预期在接近绝对零度的温度下是可测量的，其中增强的但仍然有限的（M / T）H容易忽略的固体的晶格热容。

图2.根据在0和5T磁场（空心圆，左手标尺）中测量的实验热容量数据计算的磁场中的Gd的Delta;SM从0到5T。 虚线（左侧刻度）表示绝对误差的范围，实线表示相对误差（右侧刻度）

图3.在0和5T磁场（空心圆，左侧刻度）中测量的实验热容量数据计算的磁场中的Gd的Delta;Tad从0到5T变化。 虚线（左侧刻度）表示绝对误差的范围，实线表示相对误差（右侧刻度）

早期对于在顺磁体中的磁热效应的研究是由于通过绝热退磁冷却达到超低温的驱动。 值得注意的是，Giauque和MacDougall的先驱工作，研究顺磁的低温磁热性能Gd₂（SO₄）₃）8H₂O，表明可以达到小于1K的温度。这项工作和其他对固体低温行为的重要贡献使得Giaugue赢得了1949年诺贝尔化学奖。许多年后，低温磁热效应被报道在各种顺磁盐，包括铁铵明矾，铬钾明矾和硝酸铈镁。

顺磁性盐的低热导率对于绝热退磁应用是有害的，因此顺磁性金属间化合物在它们的磁热性能方面引起一些关注。最受研究的材料之一是PrNi5，其仍然成功地用于核绝热退磁装置。结合Cu作为低温核磁退磁阶段和PrNi5作为上层，记录被设置为最低工作温度（27micro;K），在该温度下可以对材料进行有用的实验，而不是制冷剂本身。最近的实验和理论数据表明，在较高的温度（-3Klt;Tlt;-13 K），顺磁性PrNi5的磁热效应是异常的，由于结晶电场效应，导致顺磁系统在磁化时冷却去磁。

已经投入相当大的努力来研究顺磁性石榴石中的MCE，主要是因为它们具有高导热性，低晶格热容和非常低的订购温度（通常低于1K）。 随着订购温度接近绝对零度，可以获得大的Delta;SM，以保持高达20K的显着MCE。Clark和Alben报告Delta;Tad镱中Delta;H=11T接近6-10 K 和钆铁石榴石在10和30 K之间。在4.2 K的钕镓石榴石（Nd₃Ga₅O₁₂）和15K以下的钆镓石榴石（Gd₃Ga₅O₁₂）中也报道了明显的磁热效应。 Shull和他的同事最近观察到了基于铁取代的钆镓石榴石（Gd₃Ga_5〜xFe_xO₁₂（xle;2.5）的磁性纳米复合材料中的Delta;SM。

• 1. 磁热相变和有序-无序磁相变

顺磁性固体在降低温度时的自发磁性排序是协作现象，其在各种温度下发生，这取决于磁性子晶格的性质和交换相互作用的强度。当发生自发磁性排序时，固体的磁顺序参数以及固体的体积磁化在接近相应的居里或NeHel温度的相对窄的温度间隔中经历大的变化，从而导致大的（M / T）H，即使不是绝对磁化，而是磁化相对于温度的导数，其必须大于产生的MCE，4f（参见等式（2））金属（镧系元素）及其合金比3d金属及其合金更广泛地进行了研究，因为前者的可用理论磁熵远大于后者。大多数关于MCE的研究与用于例如氦和氢液化的应用，从4到77K的软铁磁材料，或者对于诸如常规空调和制冷的应用的室温附近的材料订购。本文的范围和大小不允许我们审查所有可用的数据，因此，我们将简要讨论最有趣的结果。

1.4.1低温：MCE在范围-10-80 K

低温磁性致冷剂材最自然的选择之一是在低温下有序的纯镧系金属，例如Pr，Nd，Er和Tm。如果这四种，则除了Pr（其不是顺磁性），并且未实现对大MCE值的期望。 Zimm et al报道说，Nd的MCE在T=10K时对于Delta;H=7T达到了ge;2.5K的Delta;Tad。在gt; 20和gt; 80K之间的Er中出现的几个磁相变，带来在20-90 K温度范围内几乎恒定但相当小的MCE（对于7 T磁场变化，平均值在4和5 K之间）纯Tm在~56K下以正弦调制的铁磁结构磁性排序，在~32K时变为铁磁性.Tm磁性结构的这些特征限制了其MCE，其对于Delta;H=7T在~56K上几乎不超过3K。还观察到在1T的弱磁场中，Tm中的MCE在~32和~56K之间变为负值。这些低的值的主要原因是Nd，Er和Tm中的大部分磁相是反铁磁和亚铁磁的，并且大部分熵涉及将自旋转向铁磁排列。
在~10和~80K之间显示最大MCE的材料是含有镧系金属的金属间化合物。其中最好的是RAl2，其中R=Er，Ho，Dy和Dy_0.5Ho_0.5，R=Dy_xEr_1-x，0lt;xlt;1，GdPd ，其中R=Gd，Dy和Ho。所选材料的Delta;Tad显示在图4中。很容易看出，随着温度从~10℃升高到~80 K，这与这些合金中晶格热容量的快速增加相关。在该温度范围内MCE的场依赖性从~1到~2 K/T变化。

图4.对于从0到7.5T

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[138916]，资料为PDF文档或Word文档，PDF文档可免费转换为Word