在超弹性循环下形状记忆合金中的塑性应变，最大变形应变和转变温度的变化外文翻译资料

英语原文共 10 页，剩余内容已隐藏，支付完成后下载完整资料

计算材料科学

在超弹性循环下形状记忆合金中的塑性应变，最大变形应变和转变温度的变化

摘要：对经受超弹性循环的形状记忆合金（SMA）丝的实验研究显示出显著的性能退化，包括塑性应变的累积，最大转变应变和转变温度的演变。当合金用于基于SMA的致动器和振动隔离器中时，SMA的循环降解必须仔细研究和理解。由这些问题，目前的工作旨在开发一种在考虑到由超弹性循环引起的退化下对SMA的循环效应的综合方法。新的循环本构模型是在基于亥姆霍兹自由能的热力学框架中构建的。为了解释塑性应变的演变，在正向和反向变换中单独的最大转变应变和转变温度，总累积马氏体体积分数分成两部分：在正向以及反向转换中产生的累积马氏体体积分数。基于分解，建立塑性应变，最大变形应变和变形温度的相应演变规律。最后，在我们的工作中也进行了基于提出的本构模型的数值模拟，观察到良好的相关性。

关键词：形状记忆合金 、循环退化、 本构模型、 塑性

1. 介绍

形状记忆合金（SMA）由于其热弹性马氏体转变而表现出许多特殊性质，例如形状记忆效应，超弹性（或超弹性）和阻尼[1]。 在这些热机械行为中，超弹性特别有趣。当SMA材料在高于奥氏体完成温度的环境温度下机械负载时，会显示超弹性行为。卸载后，SMA材料可恢复其初始形状并且应力应变响应显示典型的滞后环。 这个独特的超弹性促使SMA用于医疗应用，例如动脉支架，医疗导丝和导管[2]。 此外，典型的滞回环在应力应变空间中揭示了SMA是一种能量耗散材料。 利用这种性质的优点，SMA也用于隔振，例如地震隔离和机械振动隔离[3-5]。

当SMA在超弹性状态下循环时，SMA的性能将随着循环数的增加而衰减，包括塑性应变的累积和最大变形应变（也称为饱和恢复应变）的演变[ 6-8]。此外，当SMA经受重复的热或热机械负载时，转变温度将随着循环数而演变（例如超弹性循环是典型的热机械循环负载）[9-12]。特别地，在超弹性循环期间可以在SMA中产生两种塑性应变。第一个是转变诱导塑性（TRIP），其考虑了由于位错的累积，晶界错配和转变中产生的其它缺陷而产生的不可恢复的应变。第二种与在非常高的应力（例如奥氏体的屈服应力）下开始的滑移相关[13]。由于在工程应用中使用的SMA通常在合理的应力下工作，所以主要的不可逆应变是TRIP。因此，TRIP与 SMA本构模型联系更大。 为了便于理解，我们在下面几节使用“塑性应变”代表TRIP。

宫崎发现，导致塑性应变产生的位错主要在马氏体相和正向转变期间产生，因为奥氏体的滑移临界应力比马氏体的临界应变大几倍[14]。 基于这种现象，塑性应变的演变应该只发生在正向变换中，而不是都在正向和反向变换[15]。因此，本构模型中塑性应变的演化规律应与正向变换相关。

然而，现在的描述SMA的超弹性循环效应的本构模型通常假设了一个与塑性应变的正向和反向变换相关的演变规律。此外，塑性应变，最大变形应变和转变温度的演变在现有模型中几乎不被同时考虑[16-22]。

因此，本文旨在发展SMA的本构模型，考虑超弹性循环退化，包括塑性应变的累积，最大变形应变的演变和四个转变温度。 此外，不同变量的演化规律与该模型中的不同变换相关。 新的循环本构模型是在基于亥姆霍兹自由能的热力学框架中构建的。 本文的组织如下：第2节介绍通过超弹性循环实验观察到的SMA中的循环退化。考虑塑性应变，最大变形应变和转变温度的循环演变的1-D本构模型在第3节中给出，而在第4节中，数值示例被给出和讨论，结论总结在最后一节中。

为了简化表示，我们分别通过A和表示与超弹性相关的两个相，分别为奥氏体和去孪晶马氏体。 正向和反向相位变换分别由A￫和￫A表示。

1. 观察超弹性循环行为

我们对NiTi丝进行超弹性循环实验。在28℃下将金属丝反复加压至900MPa。丝的应力应变响应如图1所示，塑性应变和最大变形应变的演变如图2所示。其特征是塑性应变的演变，最大相变应变和转变温度如图3所示，并且循环降级的典型特征概述如下：

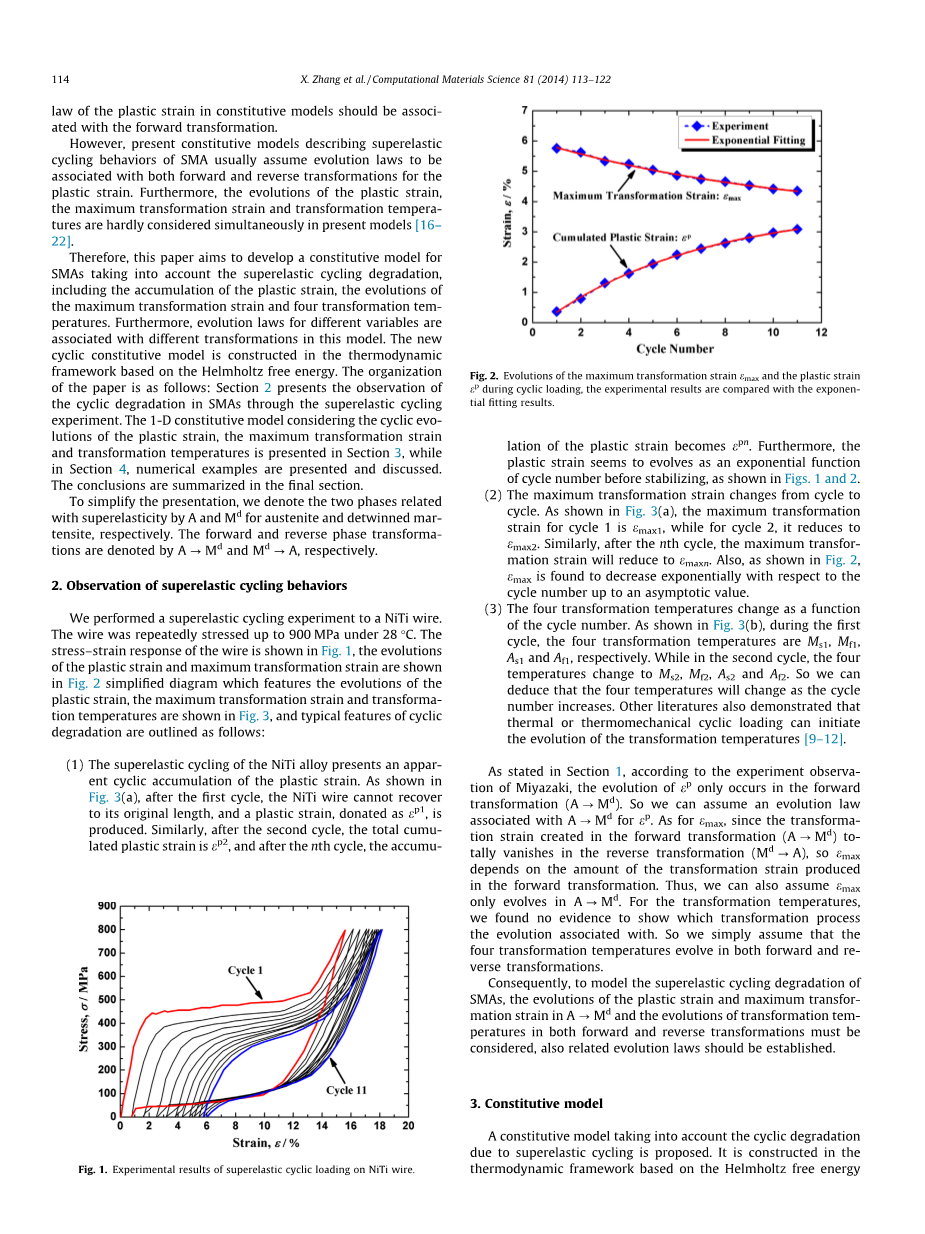
（1）NiTi合金的超弹性循环呈现明显的塑性应变循环累积。如图3（a）所示，在第一循环之后，NiTi线不能恢复到其原始长度，并且产生的塑性应变。 类似地，在第二周期之后，总累积塑性应变为，并且在第n个周期之后，塑性应变的累积变为。 此外，如图1和2所示，塑性应变似乎演变为稳定之前的循环数的指数函数。

图.1. NiTi线上超弹性循环载荷的实验结果

图.2.循环荷载下最大变形应变和塑性应变的变化，实验结果与指数拟合结果进行比较

（2）最大变形应变从一个循环到另一个循环变化。如图3（a）所示，循环1的最大变形应变为ε max1，而对于循环2，其减小到ε max2。 类似地，在第n个循环之后，最大变换应变将减小到ε maxn。 此外， 如图2所示，发现ε max相对于循环数指数地减小直到渐近值。

（3）四个转变温度作为循环数的函数而变化。 如图3（b）所示，在第一循环期间，四个转变温度分别为M s1，M f1，A s1和A f1。 而在第二周期中，四个温度变为M s2，M f2，A s2和A f2。 因此，我们可以推断出四个温度将随着循环次数的增加而改变。 其他文献还表明，热或热机械循环加载可以引发转变温度的演变[9-12]。

如第1节所述，根据宫崎的实验观察，的演化仅发生在正向变换（A→M d）中。 所以我们可以为假设与A→M d相关的演化规律。 对于εmax，由于在正向变换（A→M d）中产生的变换应变在逆向变换（M d→A）中完全消失，所以ε max取决于正向变换中产生的变换应变的量。 因此，我们也可以假设εmax只在A→M d中演变。 对于转变温度，我们没有发现证据表明哪个转变过程与演化有关。

因此，为了模拟SMA的超弹性循环降解，必须考虑A→M d中的塑性应变和最大变形应变的演变以及正向和反向变换中的变换温度的演变，还应建立相关的演变规律。

3. 本构模型

提出了考虑由于超弹性循环的循环降级的本构模型。 它在基于亥姆霍兹自由能的热力学框架中构建，以模拟SMA的热机械行为。 本构模型的结构详述如下。

3.1. 应变分解和内部变量

在无限小应变假设下，总应变ε被分解为弹性应变和非弹性应变：(1)其中，非弹性应变可以进一步分解为热膨胀应变，变形应变和塑性应变. (2) 热膨胀应变被忽略，因为该值为比其他的小得多，所以可以得到下面的表达式：(3) 如公式 （3）所示，需要两个内部变量来解释转变应变和塑性应变的演变。 通常，马氏体体积分数用作内部变量且与相关[23]：(4) 其中是最大变形应变，在[0,1]区间内马氏体体积分数是必要的

如第2节所述，塑性应变和最大变形应变仅在超弹性循环期间的正向变换中演变。 为了考虑这些演变过程，累积马氏体体积分数定义为：(5) 其中和表示累积马氏体体积分别在正向和反向变换。遵循这些定义，和可以表示如下：(6) 其中，t是运动时间，表示马氏体生成率。

发现塑性应变随着拉伸循环的数目呈指数增加直到渐近值。 此外，如第2节所指出的，假设仅在正向变换中累积。 因此，可以用假设：(7) 其中表示由于循环加载引起的累积塑性应变的饱和值。 假定为正的形状因子可以通过非线性拟合法从峰值应变对循环数的实验曲线获得。

基于第2节中的陈述，假设在循环期间在正向变换中以指数单调地演变。 因此，可以假定为：(8) 其中表示达到饱和值时的最大变化量，是循环前的初始值，可以通过超弹性循环实验获得。 形状因子可以从实验测试获得。

3.2. 自由能和转变硬化功能

多晶SMA的总亥姆霍兹自由能 [24]：(9) 其中是弹性应变能密度和。E，q分别是杨氏模量和质量密度。(11) 是热能密度，c，分别是比热容，比熵和有效比内能。 T和表示温度和参考温度。是与转换相关的能量密度。 具体地，项是与前向和反向变换相关联的能量密度。

图.3.（a）塑性应变，应力 - 应变空间中的最大变形应变和（b）超弹性循环下应力 - 温度空间中的变换温度的演变。 为了清楚起见，在应力 - 温度空间中未示出奥氏体开始和完成转变温度的演变

有效比热c在相变过程中几乎不变，因此假定它是恒定的。 但是，其他材料性质。 （10）和（11）假定为随马氏体体积分数而变化：其中上标A和M分别表示奥氏体相和马氏体相。 符号表示马氏体相和奥氏体相之间的相应材料参数的差。

是用于考虑奥氏体相和经退火的马氏体相之间的相互作用的能量密度。 在这项工作中，建立了非线性模型：其中a和b是与包括四个转变温度和临界应力的材料常数相关的本构模型参数，它们的推导将在3.6节中介绍。

3.3. 热力学和本构关系

在[25]中遵循Truesdell等人，赫尔莫兹自由能和内能u被代入热力学第一和第二定律中，得出系统状态的热力学约束，得到以下本构关系：其中，项X和Q是与和共轭的热力学力，它们是变换和塑性应变和最大变形应变演变的驱动力。 与弹性应变 和温度T相关的项具有以下表达式：SMA的热机械过程必须满足第二定律的热力学，所以耗散D必须是非 负的，被分解为固有耗散D i和热耗散D T: 其中，散热定义如下：并且所述固有耗散由亥姆霍兹自由能定义为：取等式（9）中的的时间导数，内在损耗变为：为了进一步简化等式 （25），取等式6中所示的的时间导数因此， （25）可以重写为：基于上述分析，为了满足不等式（25），必须满足不等式（26）。 因此，热力学力（X Q）必须改变符号为， 以下部分将通过Kuhn-Tucker条件满足不等式。

3.4.转换函数和Kuhn-Tucker不等式

在本模型中，假设当热力学力X达到相应的临界值时开始变换。然而，由于塑性应变和最大变形应变的演变与在正向变换中堆积的马氏体的累积同时开始，所以假定热力学力Q具有零的临界值。关于正向和反向转化的激活以及塑性应变和最大转变应变的演变的关键点总结如下。

对于正相位变换（），因为奥氏体转变成孪晶马氏体，假定为正。等式（26）可以通过假定相应的热力学里X的正值来满足。因此，对于，，X被假定为X =的临界值，基于该假设，的变换表面：当lt;0时，对于正向变换：类似地，对于反向变换（M d→A），，X和Q可以假定为和Q = 0，建议变换表面：当gt;0时，用于逆转换：其中本构模型参数和 是各个变换域的半径，这些参数的推导将在3.6节中给出。

由于热力学力必须达到相应的临界值以引起变换，因此变换函数在正向和反向变换（A→M d和M d→A）期间将满足以下条件：考虑到上述假设和约束，我们得到变换的一致性（或Kuhn-Tucker）条件，给出如下：

3.5.演化规律

通过取等式（4）和（7）的时间导数。 借助等式（8），可以得到变形应变和塑性应变的演化规律：如第2节所述，假设四个转变温度在正向和反向变换中都发展，因此总累积马氏体体积分数（在等式（5）中定义）作为控制变量以控制转变温度的演变 。 类似于塑性应变，演化规律由下式给出：其中下标0表示循环加载之前的相对参数的初始值，M fmax，M smax，A smax，A fmax分别是超弹性循环期间的相应相变温度的最大变化。 形状因子m 1，m 2，m 3和m 4可以通过非线性拟合方法从相变温度对循环数的实验曲线获得。

3.6. 本构模型参数识别程序

本文提出的本构模型有三种参数：（1）一般材料参数，（2）循环材料参数，（3）本构模型参数。 表1中列出的前两种参数可以通过实验获得。 然而，第三种参数需要通过一些识别程序来确定。

从等式（16）、（27）和（28）中可以看出，本构模型参数，包括a，b，和 需要被导出以完成本构模型。 从方程（16），（27）和（28），我们可以发现参数b和解释了正向变换，而a和 解释逆变换， 因此，我们需要考虑正向和反向变换，这是由图4所示的两个加载路径引起的 （相应的应力 - 应变曲线如图5所示），以推导这些参数。

图.4.在应力 - 温度空间中正向和反向转换的加载路径

图.5. 超弹性体系中的临界应力和相应的应变

对于相变：诱导相变加载路径是路径。如图4所示，加载路径是在恒定温度T c（T cgt; A f）下增加SMA的应力。

由于在不同温度下的加载和卸载仅执行一个循环，所以在这些模拟中不考虑循环影响，与循环退化相关的参数被设置为零。

在变换的开始，正向变换中的累积马氏体体积分数假定为，并且可以推导出以下约束：

图.7. 当T = 333K时马氏体体积分数的演变。

应力代表正向变换（）开始时的临界应力，是相应的弹性应变。 等式（8），（19）和（20）可以表示为：

图.6.在336K温度下的模拟拉伸实验结果

图.8. 在300.5K, 5.5％应变幅度, 10个循环的超弹性循环下，SMA丝的实验结果

图.9. 使用提出的本构模型模拟循环应力与应变曲线10个周期

将方程 （38） - （40）代入（27）得出下式：

图10.对于循环1，循环4和循环10的模拟与超弹性循环实验的结果。

图11.在实验结果和模型模拟之间的塑性应变和最大变形应变的演变的比较。

在转换结束时，可以推导出以下约束应力表示正转变结束的临界应力（），是相应的弹性应变。等式（8），（19）和（20）可以表示为：将方程 （43） - （45）代入（27）得出以下方程：

求解方程 （41）和（46）对于b和使用相同的识别程序，的本构模型参数 可以被给出：其中应力和表示反向转变开始和结束的临界

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[140584]，资料为PDF文档或Word文档，PDF文档可免费转换为Word