英语原文共 9 页，剩余内容已隐藏，支付完成后下载完整资料

IEEE电力输送交易，卷30，第3号，六月2015

气体放电管中的火花击穿电压脉冲避雷器

摘要：气体放电管击穿电压浪涌电压保护已被发现依赖于电压上升率, 在慢电压增加, 它接近固定电压条件，并假定为击穿在一个给定的关于帕邢定律电压,偏差平稳的放电电压测量测试样本分配的电极条件的变化，并说明为汤森德系数(r)的影响。冲量增加放电电压在电压快速上升取决于滞后的时间火花击穿的统计和形成的影响评估时间滞后, 作为离子雪崩和流光的起源的形成，冷场的电子发射过程被认为对于稀有随机事件的泊松概率函数关注发射电子流的评价, 由于有关系统参数缺乏适用值脉冲放电电压和的关系模拟得到的电压上升率或多或少具有定性特征, 仿真系数取值选择拟合的模拟结果测得的, 它们的相关性进行了验证，通过比较它与典型值在文献中发现的排放量.

指数期货的击穿概率，气体放电管，冲击放电电压，放电，放电电压、统计时间滞后。

1. 简介

浪涌保护电路过压气体时的放电，放电管（GDT）保护, 在一定的点火或放电电压之间出现的开路工作电压和保护电平电压, GDT电极之间的放电电压降低基本上低于保护水平，甚至低于正常电路电压, 在功率电路中，它减小到200伏左右当放电电流不超过0.3 A的一些或

20 V的其他电流高于1A.

GDT的施工比较简单，因为它是由至少两电极连接到保护电路不同电位线之间；两种不同

概念见图1。三分之一电极有时添加为了帮助GDT放电, 电极系统是一个普通的真空密封在一个特定的气体介质（惰性气体，如氩，氖，或它们的混合物）压力和电极由间隙隔开，在那里放电发生,立即点燃后，辉光或电弧放电开发的放电电流的大小保持电极之间的间隙电压在100 V和V的大小的订单，分别[ 1 ]为了模拟GDT在电压脉冲响应，一线性增加电压施加由于简化计算程序。模拟的目的是获得GDT放电点火的定性模型基于相关物理现象

以下故障理论首次提出，这是论文的本质的数学模型。它的推导在下一节，其中三例脉冲放电电压上升分别处理

在本文的最后一部分，模拟的结果数学模型，并与测量结果进行比较。我们的目标是使用该模型来确定在选定的火花击穿的统计概率电压上升和峰值电压

图1,GDT的建设原则

1. GDT击穿

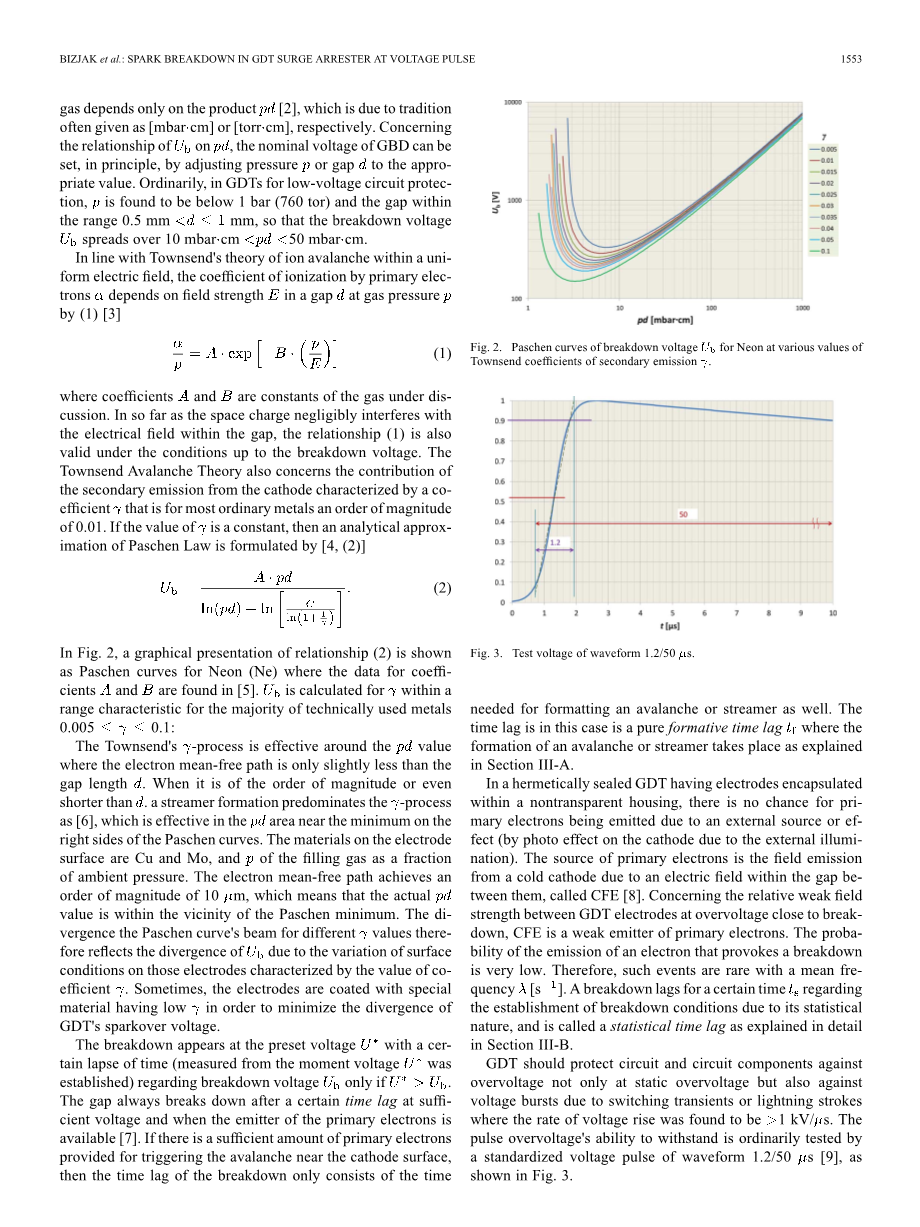
由于其保护功能，最高允许通过电压U_P不应超过保护级别,GDT工作电压是用容忍偏离其额定电压分配按产品标准20%。标称电压是由火花放电电压U*在静止条件下,接近击穿电压U_b关于压力和化学的封装气体混合物组成和电极间的间隙。火花放电电压U*在一个非常缓慢的增加电压总是提供大小在略高于U_b测量.由于保持和常数的随机效应，具有一定的耗散性。根据帕邢定律,在规定的气体击穿电压U_b只取决于产品pd[ 2 ]，这是由于通常分别用[厘米]或[乇毫巴厘米]。关于U_b与pd的关系，GBD的标称电压可设定，原则上，通过采用调整压力p或间隙d到适当的值。通常，GDT的低压电路保护，被发现是低于1杆（760吨）和间隙范围内0.5mm＜d＜1mm，使击穿电压分布在50毫巴厘米gt;pdgt;10厘米毫巴。符合汤森德的离子电场雪崩理论，一次电子电离系数取决于气体压力p在气隙磁场强度（1）[ 3 ].

(1)

系数A和正在讨论中的气体常数B,在迄今为止的空间电荷可以忽略干扰的间隙内电场的关系（1）也是有效的条件下达到击穿电压。汤森德雪崩理论还涉及从阴极的二次发射的贡献，其特征在于由一个系数r，这是对于大多数普通金属的一个数量级0.01。如果该值r是一个常数，那么Paschen Law的解析近似是由[ 4（2）]制定的.

(2)

在图2中，图示的关系（2）显示至于霓虹Paschen曲线（NE）在数据的系数

A和B是在[ 5 ]。U_b计算范围为大多数技术上使用的金属的范围内的特性

汤森德的过程是有效的在pd值，电子的平均自由路径仅比间隙长度d略少。当它的数量级甚至小于d。流光形成占主导地位的过程[ 6 ]，这是在附近的最低pd地区有效的Paschen曲线的右侧。在电极表面的材料是Cu 和 Mo,，和p的填充气体环境压力的一部分,电子的平均自由程达到10米一个数量级，这意味着实际pd值在Paschen附近最小。不同的r值发散的帕邢曲线梁因此反映U_b由于地表条件变化对电极由系数r价值的分歧.有时，电极涂层以减少放电管的击穿电压的差异具有低r特殊材料。

故障出现在同一段时间预置电压U*（从目前电压U*测量成立）的击穿电压U_b只有U* gt; U_b。该间隙总是打破一定的时间滞后后，在足够的电压，当主电子发射器可用[ 7 ]。如果有触发的阴极表面附近的原电子雪崩提供足够量的时间滞后，然后崩溃只包含所需的时间格式雪崩或流光.时间滞后在这种情况下是一个纯粹的形成时间滞后的地方形成了雪崩或流光发生在第iii-a.解释.在一个密封的GDT具有电极封装在一个不透明的住房，也没有机会为主要的电子被发射由于外部电源或效果（由光电效应在阴极由于外部照明）。初级电子场发射源是由于电场冷阴极在它们之间的间隙，称为CFE [ 8 ]。关于相对弱场强电极之间的电压接近击穿GDT，CFE是初级电子的弱发射。激发击穿的电子的发射几率很低。因此，这样的事件是罕见的平均频率lambda;[s^-1].故障滞后有关故障条件下由于其统计性质的建立一定的时间ts，又称为统计时间滞后详细解释第iii-b.

GDT应该保护电路和电路元件的过电压不仅在静态电压也对电压脉冲由于瞬变或雷击，升压率被发现大于1 kV /秒脉冲过电压的承受能力是由一个标准化的波形1.2/50我们[ 9 ]电压脉冲通常测试开关，如图3所示。

图4。击穿峰值由于放电电压波形的一1.2/50不同幅值的火花放电模拟（见插图）。

图5,传导测量的测量方案

图6。在静态测量试验电压的上升率100 V /s和1 kV / us(U_p)对测试样本集放电电压U*。

由于其特定的时间滞后，即为电压脉冲响应变化的电压上升率。巨大的放电电压和工作时间为响应GDT标准电压脉冲1.2/50在不同峰值示插图在Fig.4在指定故障电压U_b=400V[ 5 ].当超过击穿电压U_b在各种放电出现.击穿发生在峰值以下，U_p积分波形U(t)-U_b在时间间隔到崩溃的时刻的规则（U(t)=U_p）应是一个恒定的脉冲幅度。击穿后，电压降低到辉光或电弧电压（如图4所示）。

一种过电压脉冲响应时间相对较长的滞后特性的GDT相比其他类型的过电压保护元件（压敏电阻、二极管等），但它能够承受高电流脉冲在雷击。

1. 击穿数学模型GDT的过程

为了避免复杂的计算程序，这是一个趋势，创造一个GDT的击穿的物理模型时，基本的物理现象和规律进行分解过程的数学模型。一个斜坡形式的电压脉冲具有不同的上升率，用于模拟电压浪涌被用于定性呈现击穿特性的目的。

关于估计形成的时间滞后，少量的过电压theta;关于U_b采用汤森德雪崩模型，虽然故障可能出现在物质上的theta;价值高。对于故障与theta;用于仿真的形成时间的数学关系被认为是相当于Argon由于其相似的其他惰性气体，但随着系数的不同的值。

统计时间滞后，通过计算发射来自稀有事件的泊松过程的CFE电子的概率估计。在文献中找到的参数精度差评价CFE和电离在GDT；因此，相关参数的值必须通过拟合计算结果与测量值确定。

1. 冲击放电电压上升由于形成时间滞后

当火花电极之间的电压瞬间提升到一个恒定值时U* gt; U_b，只要有大量的初级电子可用于雪崩的开始，然后会发生击穿后U* 形成的时间t_f的推移。连续地，火花电极之间的电压将急剧下降到电压的自持放电，无论是辉光或电弧.形成的时间t_f是一个分数过电压theta;函数，定义在[ 7 ]为

(3)

范围内的0.01lt;theta;lt;0.3，形成的时间t_f是成反比的大多数气体

(4)

在常是气型。在过电压分数theta;，（5）更充分说明这个关系是（4）

（5）

在这情况下，指数beta;延伸0.5和2之间。方程（4）冰条件的有效期为那些靠近汤森的雪崩电离的案例，但在不断增长的流光电晕的形成有影响，从差（4）（5）增加[ 6 ]。在两个特定方面的研究报告，在缺口上d 增加1毫米，汤森r过程可能是显性的[ 5 ]。

实验结果表现层的形成时间在[ 6 ]是通过电极与照明城市紫外，在离第一部少10 ns辐射空调的地方电极的应用，因此，这个初始期间被排除在形成放电时，然后，形成的时间t_d，来自测量，接近t_f电极调节的时间是可以忽略不计的比较时，辐照和崩溃的那一刻开始之间的时间间隔.实验发现的关系类似于（5）被描述为:

(6)

在氩a=20us.

窗体顶端

窗体底端

关于有效性（6），形成的时间也可以进行评估的情况下，电压U脉冲在时间作为一个功能U(t)和分数过theta;以及瞬时电压增大.在一个适度的增加U，电离所得的温度T增加半平稳热过程。因此，预击穿电流i随之增加，直到T达到一个临界值T_C，和i的临界值I_C，造成后时间的推移故障t_d，制定

(7)

在（7），值也有所不同，如图所示

(8)

一般来说，时间t应计算从故障的条件刚刚完成，然后进一步维护的时刻。在电压斜坡的情况下，有一个恒定的上升速度k，并从零开始在某一时刻,这是方便（8）涉及时间trsquo;计数的时候电压u刚过U_b由于故障没有发生在较低的值.所以U(trsquo;)=k*trsquo;,关于trsquo;=0时U(trsquo;=0)=U_b且U(trsquo;)gt;U_b.关系（8）然后达到形式

(9)

只要保持平稳的热条件下，以（9）、关系（10）可以由表达式（7），其中关键的预击穿电流I，一般，一个功能theta;和trsquo;，或他们的产品#甚至一个函数theta;*trsquo;.的关系（10）也为t_d指定是有效的

(10)

在指定气体已知值的地方。在电压斜坡t_d的情况下，当它满足条件时形成的击穿时间（11），在材料常数击穿电压U_b被称为指定的气体电极系统电压上升率k

(11)

当电压斜坡U(t)的波形由线性函数,关于时间坐标t=0时U(t)=0，在给定的k,斜坡值达到U_b此刻t_b和t_b形成击穿后的时间，它发生在斜坡时间t_p，制定

(12)

通过插入计算值t_p,成线性关系的斜坡在指定k,一个故障U_p斜坡值获得

(13)

方程（13）表明斜坡击穿发生在上述U_b在陡峭的斜坡击穿发生在更高的电压，由于时间滞后电压。模拟结果如图7所示。

B.冲击放电电压上升由于统计时间滞后

当气体电极系统在击穿条件下的主电子的来源是不存在的或阴极的照射是无法释放电子，击穿有时触发由外部粒子解放启动电子。在真空密封的封装类型GDT此类事件的频率是罕见的，可以忽略不计，如图1所示。在这种情况下，它被证实，电流通过电极间隙的电压取决于与他们根据[ 10 ]密立根–Lauritzen的关系，表明初级电子从冷阴极发射场（CFE）。

CFE的过程是由Fowler–Nordheim理论描述，适用于解释场发射电子枪的操作在一个真空以及真空开关击穿之间的接触甚至之间紧密排列在气体[ 4 ]电接触的初始阶段,在这些情况下，修改原有的常规理论简称CFE–经常被应用，如制定[ 11 ]

(14)

在C₁和C₂经验确定的CFE系统参数。对于原来的F-N理论，指数的k值等于2.但经验值靠近k=1.2[12][13],C2中的系数C1也依赖于阴极表面的电子功函数phi;:

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[27265]，资料为PDF文档或Word文档，PDF文档可免费转换为Word