FDTD模拟水平接地电极及其等效电路建模外文翻译资料

英语原文共 9 页，剩余内容已隐藏，支付完成后下载完整资料

FDTD模拟水平接地电极及其等效电路建模

Masanobu Tsumura, Yoshihiro Baba, Member, IEEE, Naoto Nagaoka, Member, IEEE, and Akihiro Ametani, Fellow, IEEE

摘要：利用有限差分时域（FDTD）方法计算电流导线和电压参考导线的三种不同布置中的水平接地电极的瞬态响应求解麦克斯韦方程。测试布置不会影响水平接地电极的瞬态响应。 使用用于Sunde等效电路的电磁瞬态程序（EMTP）计算的瞬态响应与使用FDTD方法计算的相应响应相当好，除了在水平接地极的闭合端（到激励点）的电压的初始上升部分。等效电路的EMTP计算响应（被修改以改善这种差异）更好地与相应的FDTD计算的响应一致。

索引术语 - 电磁瞬态分析，等效电路，有限差分法，接地电极。

一、介绍

通过将故障电流耗散到地中，接地电极防止电信和电力系统的设备被损坏。因此，为了优化这些系统的防止过电压和故障电流的保护装置，有必要知道瞬变和接地电极的稳态特性。

通过实验（例如，Liew和Darveniza [1]; Sekioka et al[2]; Ametani et al[3]）和最近通过基于时刻法（有限元法（FEM）和Yee [7]和Taflov和Hagness [8]的用于求解麦克斯韦方程的时域有限差分（FDTD）方法）的数值电磁分析（例如Grcev和Dawalibi[4]; Liu et al[5]; Tanabe[6]）研究了接地电极的瞬态和稳态特性。可以假定地面的电导率和相对介电常数的任意值来进行数值电磁分析。这样的结果对于理解现象以及确认测量结果是有用的。虽然数值电磁分析具有上述优点，但是它们通常需要长的计算时间和大量的存储器。因此，它们限于小空间的分析，并且不能用于分析大型电信和电力系统中的瞬态现象。对于这种大系统中的瞬态分析，基于等效电路的计算更合适。

在本文中，使用FDTD方法计算电流导线和电压参考导线相对于水平接地电极的三种不同布置中的水平接地电极（称为平衡）的瞬态响应，并且找到这三种安排中最适当的一种。然后，使用用于Sunde等效电路（Sunde [10]）的电磁瞬变程序（EMTP）（Scott-Meyer [9]）计算的响应与使用FDTD方法计算的相应响应进行比较，并且讨论响应中的差异。等效电路的EMTP计算的响应（Yamaguchi et al[11]）也与相应的FDTD计算的响应进行比较，确定其电路参数的值。在附录中，将两个不同接地电极的FDTD计算响应与相应的测量值进行比较（[6]，Tanabe et al[12]），以测试作者的FDTD计算的有效性。注意，在本文中，土壤被假定是均匀和非分散的，虽然Teixeira et al [13]在地面穿透雷达的FDTD分析中成功地表示了使用分段线性递归卷积技术的土壤色散。还要注意，在大电流注入下发生的非线性效应（例如，[1]，Chisholm和Janischewskyj [14]）在本文中没有考虑。

二、FDTD计算

A、模型

在测量水平接地电极的瞬态响应时，已经使用了水平电流导线和水平电压参考线（例如[2]，[3]，[6]，[11]，[12]）。尽管希望将水平导体彼此垂直放置以减少不期望的导入，但是这种布置不能在水平面上实现。在本节中，使用FDTD方法研究了电线布置对水平接地电极响应测量的影响。本节的目的是在测量中显示合理布线，尽管在FDTD计算中因为可以对电场进行积分评估而不需要用于评估接地电极电压的电压基准线。请注意作者的FDTD计算的有效性在附录中得到证明，其中将两个不同接地电极的FDTD计算响应与相应的测量结果进行比较[6]，[12]。

图1显示了要测试的测量中的三个代表性安排。在布置1中[如图1（a）所示]，接地电极平行于电流导线放置，并与电压基准线垂直。在布置2中[如图1（b）所示]，接地电极垂直于电流导线和电压基准线放置，其中电流导线从电压参考线拉伸。在布置3中[如图1（c）所示]，接地电极平行于电压参考线放置，并与电流导线垂直。

图1.使用FDTD方法分析长度为1.5m的水平接地电极的瞬态响应测试安排的侧面和平面图。（a）布置1（b）布置2（c）布置3。

水平接地电极的长度，其半径及其埋深分别设定为1.5m，7mm和0.1m。水平电流导线的长度，其半径和高度分别设定为8m，23mm和4m。水平电压参考线的长度，其半径和高度分别设定为8m，23mm和0.1m。当水平电流导线和电压参考线的长度设置为16m时，FDTD计算的响应与长度和水平电流导线和电压参考线的长度等于8m的情况没有太大的不同。水平电流导线的远端与埋入部分为1m的垂直导线连接。导线的近端通过与集总电流源串联连接的类似的垂直导线（空中）和相对介电常数与土壤相同的绝缘导线（空气/接地界面下方）与水平接地电极连接。该垂直导线与水平电压基准线之间有0.1m的间隙。电流源产生具有1A的幅度和7ns的上升时间的斜波。地面的导电率，相对介电常数和相对磁导率分别设定为sigma;=7.5mS/m，ε_r=20，mu;_r=1。20mtimes;20mtimes;20m的工作体积分为0.1mtimes; 0.1mtimes;0.1m立方块，并被廖氏二阶吸收边界条件的六个平面包围(Liao et al. [15])。执行最多0.5mu;s的计算，时间增量为0.0962ns。当使用具有3.8GHz Pentium 4处理器和3GB内存的个人计算机时，计算时间约为4小时。

在FDTD程序中用零半径的线（通过强制沿线的轴线的电场切向分量为零）模拟电流导线和半径为23mm的电压基准线，其横截面积为0.2mtimes;0.2m，相对介电常数ε_r为0.390，相对磁导率mu;_r为0.390（Noda和Yokoyama [16]）。类似地，半径为7mm的水平接地电极由嵌入截面积为0.2mtimes;0.2m，导电率sigma;为0.296S/m，相对介电常数ε_r为0.296，相对磁导率mu;_r为0.296的矩形棱镜的零半径线表示(Baba et al. [17])。

B、计算结果

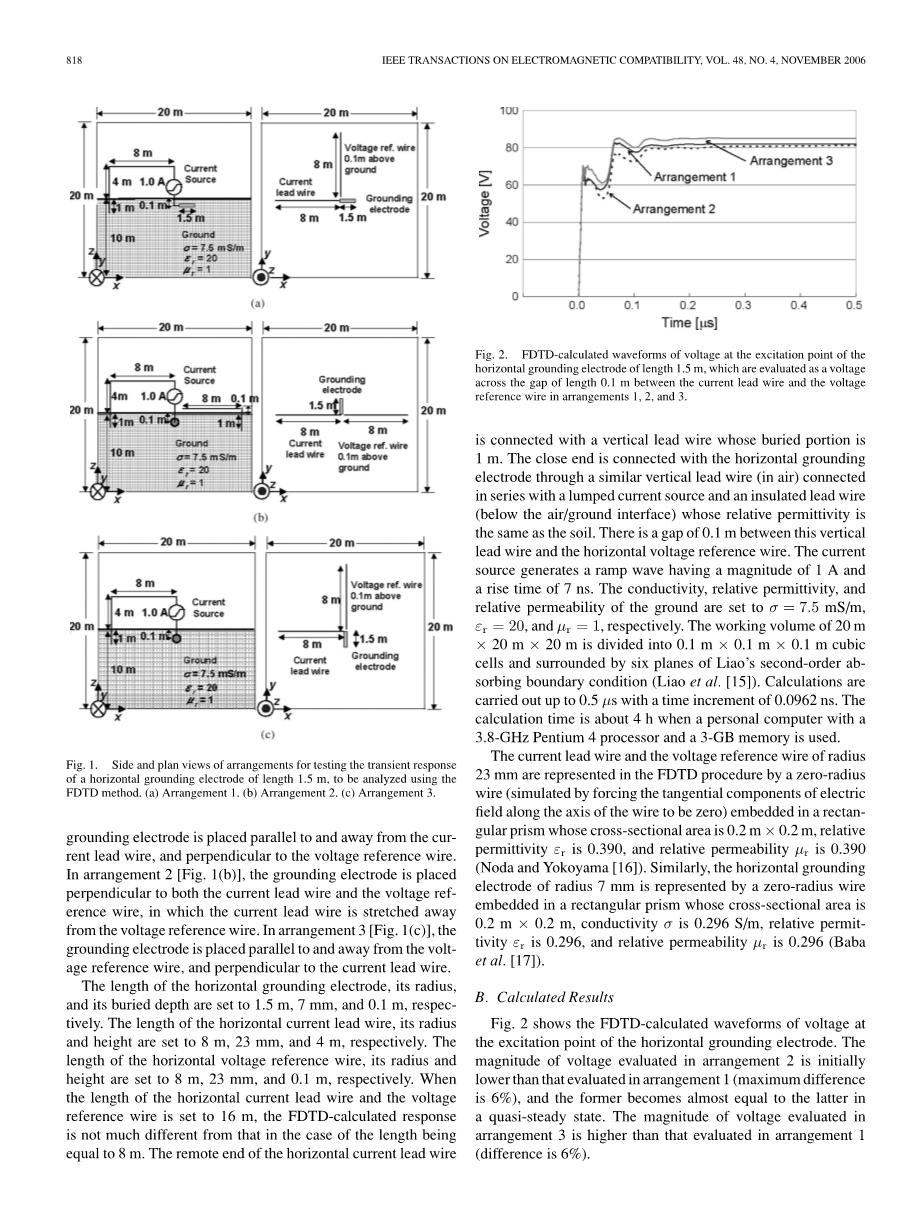
图2展示了在水平接地电极的激发点处的电压的FDTD计算波形。布置2中评估的电压幅度初始低于布置1中评估的电压的大小（最大差异为6％），并且前者在准稳态下几乎等于后者。在布置3中评估的电压的大小高于布置1中评估的电压的大小（差异为6％）。

图2 长度为1.5m的水平接地电极激发点的电压的FDTD计算波形，其中电压为布置1、2、3中被评估为电流导线与电压参考线之间的长度为0.1m的间隙上的电压。

C、讨论

图3 （a）布置2和（b）布置3中沿着水平电流导线和水平接地电极传播的电流波产生的轴向电场方向示意图。

虽然测试装置对评估的瞬态响应的影响不显著（6％），但沿着电流导线和本节中的水平接地电极传播的电流波的相关轴向电场定性地解释了评估电压差异的原因。

图3展示了沿着电线和相关电场的电流波示意图。图3（a）示出了布置2的侧视图，其中水平电流导线平行于和远离水平电压参考线放置，并且它们都垂直于水平接地电极。在这种布置中，从电流源向左传播的负电流波产生左向电场。该电场抑制垂直电流导线与水平电压基准线之间的间隙上的电压。这就是为什么在布置2中评估的电压的大小最初低于布置1中评估的电压的原因。

图3（b）展示了布置3的侧视图，其中电压参考线平行于和远离水平电压参考线放置，并且它们都垂直于水平电流导线。在这种布置中，沿着水平接地电极向左传播的正电流波产生正向电场。该电场增加了垂直电流导线和水平电压参考线之间的间隙上的电压。这就是为什么布置3中评估的电压的大小高于布置1和2中评估的电压的大小。在布置3中评估的准稳态中的电压高于布置1和2中评估的电压的原因是可能是由于布置3（并联）中的接地电极和电压参考线的布置与布置1和2（垂直）不同。

从上述可以看出，在测量水平接地电极的瞬态响应的三种布置中，布置1是最合适的，因为它受到不期望的轴向电场的影响最小。然而，由于测试布置的差异而导致的评估电压幅度的差异仅为6％。请注意，在FDTD计算中，电压可以在不使用参考电压的情况下对电场进行积分。在不存在电压基准线的情况下，从吸收边界到激励点的水平电场（平行于y轴）的电压波形几乎与垂直电流导线与电压基准线之间的间隙电压一致，如图4所示。

图4 布置1的长度为1.5m的水平接地电极的激发点处的电压的FDTD计算的波形被认为是电流导线和水平电压参考线之间的0.1m间隙上的电压，值为对从吸收边界到激发点的水平电场进行积分。

1. 针对当前等效电路的EMTP计算

A、FDTD模型

在本节中，为了测试Sunde等效电路的有效性[10]，将该等效电路的EMTP计算响应与图5所示配置中的水平接地电极的FDTD计算响应进行比较。水平电流导线的长度，其半径和高度分别为15m，6mm和2m。水平电流导线的远端连接到垂直导线，并且近端通过与集总电流源串联连接的半径为6mm的垂直电流导线连接到水平接地电极（空气中）和导体半径为6mm（空气/接地界面以下）的绝缘导线。该电流源产生具有1A的幅度和7ns的上升时间的斜波。接地电极上一点的电压是从吸收边界（距接地电极55m）到该点的水平电场的积分。空气中和地面上半径为6mm的电线使用第二部分所述的相同方法表示。60mtimes;80mtimes;35m的工作体积分为0.25mtimes;0.25mtimes;0.25m的立方块，并被廖氏二阶吸收边界条件的六个平面包围[15]。计算时间可达0.5或1mu;s，时间增量为0.240 ns。

B、Sunde的等效电路

Sunde [10]得出了水平接地电极的电导G₁和电容C₁的表达式，如下：

(1)

其中sigma;是地面的电导率，是介电常数的真空度，是地面的相对介电常数，l是水平接地电极的长度，r是其半径，d是其埋深。等效电路如图6所示。

图六 Sunde的水平接地电极的等效电路

C、比较与讨论

图7（a）表示在图5所示的结构中使用FDTD方法计算出的水平接地电极的端部（表示为点A）和其中心点（表示为点B）的波形，利用EMTP为图6所示的Sunde等效电路计算。图7（b）表示电流波形。水平接地电极的长度（l）为5m，半径（r）为10mm，埋深（d）为1m。地面的电导率和相对介电常数分别设定为sigma;=7.5mS/m和=10。在EMTP计算中，使用（1）计算出的G₁和C₁（36.2mS和0.427nF）。使用“电缆参数”程序（Ametani[18]）以1MHz的频率计算图6所示电路的分布线部分的常数。注意，在该计算中，水平接地电极被认为是具有=10，芯导体半径（r）为10mm，壳体导体半径为的绝缘电缆。确定的值，使得电缆的芯和护套之间的电容等于（1）给出的C₁。还要注意，长度为5m的水平接地电极由图6所示电路的五个串联连接表示（每个长度为1m，分布电路部分的特性阻抗为130Omega;，每个集线电导率为7.24mS=36.2/5mS）。

图七 使用用于Sunde等效电路的EMTP计算的水平接地电极的不同点和使用FDTD方法计算的水平接地电极的不同点的电压波形图（a）及电流波形图（b）（l=5m，r=10mm，d=1m，sigma;=7.5mS/m和ε_r=10）。

电压急剧上升，然后随时间缓慢下降。该特性被称为“感应”特性（例如，Tanabe [19]），并且当地电导率高时趋于发生。在FDTD计算电压和电流波形两者中观察到的0.15mu;s周围的突起是5m长接地极的远端的反射。

图8（a）和（b）分别为sigma;=1mS/m，=10和sigma;=7.5mS/m，=2时的同一接地电极的电压波形。在图8（a）和（b）的EMTP计算中，5m长的接地电极以与上述相似的方式表示。分布线部分的特征阻抗分别为130和280Omega;，每个元件的集总电导分别为0.965和7.24mS。与图7（a）所示的不同，电压随时间相当缓慢上升到峰值，然后保持稳定。这个特性被称为“电容”特性[19]，并且当地电导率低时，往往会发生这种特性。

虽然使用EMTP为Sunde等效电路计算的电压和电流的波形与使用FDTD方法计算的电压和电流波形吻合良好，但对于Sunde电路计算的A点电压初始峰值比使用FDTD计算的初始电压峰值高出10％-20％方法。

在下一节中，将修改后的等效电路[11]的EMTP计算响应与相应的FDTD计算响应进行比较，电路参数的值将使修改电路在更好的情况下再现FDTD计算的响应确定方式（波形和磁场）。

图8 使用用于Sunde等效电路的EMTP计算的水平接地电极的不同点处的电压波形和使用FDTD方法计算的电压波形，其中（a）图：sigma;= 1mS/m和= 10，（b）图sigma;= 7.5mS/m，= 2。

1. <st

   剩余内容已隐藏，支付完成后下载完整资料

   ---

   资料编号：[26118]，资料为PDF文档或Word文档，PDF文档可免费转换为Word

   </st