表征复杂网络的社区结构外文翻译资料

英语原文共 9 页，剩余内容已隐藏，支付完成后下载完整资料

表征复杂网络的社区结构

作者：Andrea Lancichinetti, Mikko Kivelauml;, Jari Saramauml;ki, Santo Fortunato

摘要

背景：社区结构是复杂网络的关键特征之一，在人类学和功能上起着至关重要的作用。 虽然在社区检测问题上已经做了大量工作，但迄今为止，很少关注真正网络社区的调查工作。

方法/主要结果：本文对大型信息，通信，技术，生物和社会网络中社区的统计特性进行了系统的实证分析。本文发现相同类别的网络的介观组织是非常相似的。这反映在社区结构的几个特征中，可以被用作特定网络类别的“指纹”。虽然社区规模分布总是广泛的，但某些类别的网络主要由树状社区组成，而其他类型的网络则更为密集。社区内的平均路径长度最初以社区规模对数增长，但是对于大于特征大小的社区，增长饱和或减慢。此行为与社区中的中心的存在相关，其角色在不同类别之间有所不同。另外，根据社区内的链接分数来衡量节点的社区嵌入度，每个类别都有一个特征分布。

结论/意义：本文的研究结果通过使用两种根本不同的社区检测方法进行验证，允许对真实网络进行分类，并为网络演化的现实建模铺路。

引言

复杂系统的现代科学经历了一个重大的进步后发现复杂系统的图表示方法，尽管它很简单，但也能揭示一些关键特征，并足以揭示其一般结构特性，功能和演化机制。将复杂系统表示为图形意味着将系统的基本单元转换为节点，而节点之间的链接则表示其相互之间的交互或关系。许多复杂网络的特征在于节点的邻居数量的广泛分布，即其度数。作用是研究特殊属性，如随机故障的高度鲁棒性，以及流行病传播的门槛缺乏性。

复杂网络的另一个重要特征是通过它们的介观结构来表示的，其特征存在于称为社区或模块的节点组，这些节点组具有高密度的同一组节点和不同组的节点之间的链接相对低密度之间的关系。在不同来源的系统中网络的这种分隔组织非常普遍。在20世纪60年代就有人指出，分层模块化结构对于复杂系统的鲁棒性和稳定性是必要的，并且给它们带来进化上的优势。

探索网络社区的重要性主要有三个原因：1）以粗略的方式揭示网络组织，这可能有助于为其起源和演化制定现实的机制; 2）更好地了解网络上发生的动态过程（例如，流行病学和创新的传播过程），这可能会受图形模块化结构的严重影响; 3）通过检查一个整体的图形来发现节点之间不明显的关系，一般由系统的功能来实现。

所以近几年来，图形社区结构研究的爆炸式增长不足为奇。当然，如今主要的问题是如何发现社区，这是大多数文献中的论题所提出的重要问题。尽管已经设计了大量的方法和技术，但科学界还没有商定哪种方法最可靠，什么方法应该或不应该采用。这是因为社区的概念是不明确的。由于侧重点在方法的设计上，迄今为止很少有人做出努力来解决这一根本问题：真实网络中的社区是什么样的？这是本文将尝试评估的。

调查显示，在广泛的网络中，社区规模的分布是广泛的，许多小社区与大社区共存。两者的分布通常可以很好地适应幂律。 Leskovec et al.对实际网络中的社区质量进行了全面的调查，以电导分数为依据。他们发现，在特征大小为100个节点的社区中，最小的电导表明存在明确的模块，而大社区与网络的其余部分“混合”。因此，他们认为网络的介观组织可能具有核心—外围结构，其外围由小型明确界定的社区组成，核心包括较密集的模块，彼此密集连接，导致难以检测。 Guimeraacute;和Amaral则提出了可以根据社区中角色来对节点分类。

然而，真实网络中社区的基本属性仍然是未知数。揭示这些属性是本文的主要目标。为此，本文对自然界，社会和技术界的许多真实网络的社区结构进行了广泛的统计分析。主要结论是，社区具有鲜明的特征，这对于同一类的网络是常见的，但是从一个阶段到另一个阶段是不同的。值得注意的是，这种表征独立于找到社区所采用的具体方法。

方法

本文的目标是研究社区的统计特征，需要在包含大量不同社区的大型网络上采用数据集。本文的数据集包含10⁵-10⁶个节点，蛋白质相互作用网络（PIN）除外，其中最大的可用数据集是10⁴个节点的数量级。

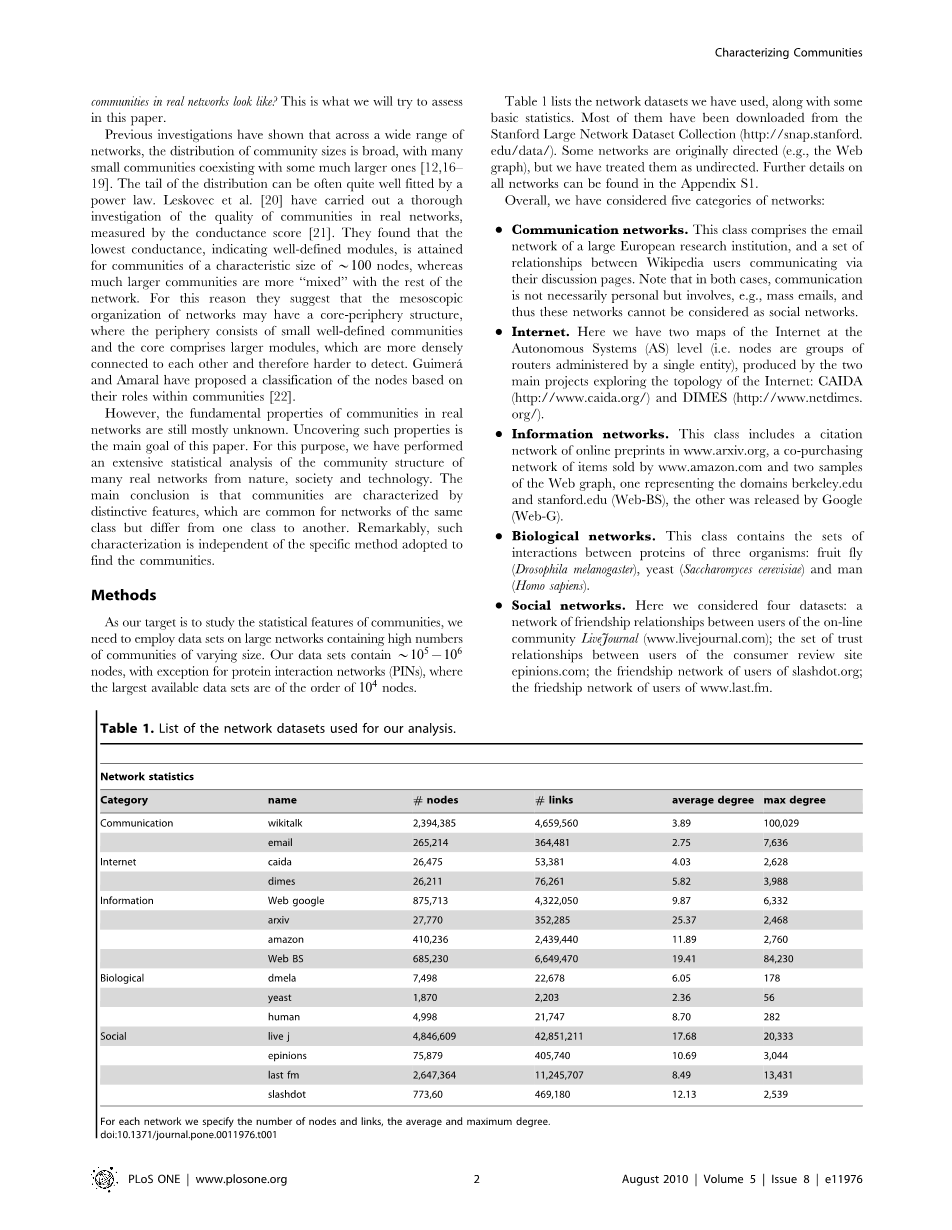
表1列出了本文使用的网络数据集，以及一些基本的统计信息。大多数都是从斯坦福大网络数据集（http://snap.stanford.edu/data/）上下载的。一些网络是有针对性的（例如，Web图表），但是本文还是将这些网络视为无向的。有关所有网络的更多详细信息，请参见附录S1。

总体而言，本文列出了五类网络：

• 通讯网络 这一类别包括一个大型欧洲研究机构的电子邮件网络，以及通过他们的讨论页面进行通信的维基百科用户之间的一组关系。注意，在这两种情况下，通信不一定是个人的，而是涉及例如大量电子邮件，因此这些网络不能被认为是社交网络。
• 互联网 在这里有两个自治系统（AS）级别的互联网地图（即节点是由单一实体管理的路由器组），由浏览互联网拓扑的两个主要项目生成：CAIDA（http：// www .caida.org /）和DIMES（http://www.netdimes.org/）。
• 信息网络 该类别包括在www.arxiv.org上的在线预印本的引用网络，在www.amazon.com上所出售的项目的共同采购网络和Web图表的两个示例，一个代表域名berkeley.edu和stanford.edu（ Web-BS），另一个由Google（Web-G）发布。
• 生物网络 这个类别包含三种生物的蛋白质之间的相互作用集：果蝇（黑腹果蝇），酵母（酿酒酵母）和人（智人）。
• 社交网络 在这里本文考虑了四个数据集：在线社区LiveJournal（www.livejournal.com）的用户之间关系网络; 消费者评论网站epinions.com的用户之间的信任关系;slashdot.org的用户关系网; www.last.fm的用户网络。

表1.用于分析的网络数据集列表

对于每个网络，本文指定节点和链接的数量，平均度和最大度。

doi：10.1371 / journal.pone.0011976.t001

选择检测社区的方法是一个非常微妙的问题。首先，需要非常有效的算法，因为本文研究的网络很大。这个要求排除了大多数现有的方法。第二，如上所述，关于多用途社区检测方法没有共同的协议。因为没有社区的共同定义，这是由于问题本身的性质所决定的。因此，在定义算法的可靠测试程序方面也存在任意性。尽管如此，Condon和Karp的文章最初对介绍的社区定义也有着广泛的共识。这个共识是，如果相同社区的两个节点相连的概率超过了不同社区的节点连接的概率，则网络具有社区。社区的这一概念已被采用，以创建社区的基准图，如由Girvan和Newma引入的图表以及Lancichinetti等人最近设计的图表。 将Girvan和Newman的基准测试中实际的度和社区规模（LFR基准）分布进行整合。最近的工作表明，一些算法在LFR基准上表现非常好。尤其是由Rosvall和Bergstrom引入的Infomap方法具备出色的性能，并且反应也很快，因此适用于大型网络。然而，由于每个社区检测方法都有自己的“风味”，并且倾向于将某些类型的结构标记为社区，如果要提出关于社区结构的一般结论，依靠单一方法是不够的。因此，我们将Infomap获得的结果与Leung等人提出的标签传播方法（LPM）这两种不同的算法进行了交叉检验。后者已被证明在LFR基准上是可靠的，并且也足够快能够处理本文收集的最大系统。详细描述Infomap和LPM在附录S1中给出。这里本文只是指出两种技术之间的深刻差异。 Infomap是一种全局优化方法，其目的是优化表达图上无限长随机游走的代码长度的质量函数。 LPM是一种局部方法，节点被归结为与其邻居大部分相同的社区。通过两种方法为同一网络获得的分区通常不同。然而，社区结构的一般统计特征似乎并不取决于分区的细节。以下只提供Infomap的结果;对于LPM，请参见附录S1。

结果

本文通过简要讨论社区大小的分布来开始分析（图1）。本文看到，正如预期的那样，对于每个系统来说，社区规模范围很广，跨越了最大系统的几个数量级。这与早先的研究结果一致。分布的整体形状在同一类的系统中是相似的。生物网络的分布显示出最大的差异，然而，由于网络较小，这些差异可能由噪声引起。对于生物网络，用LPM进行的分析显示略有不同，是重叠的分布（见附录S1）。

图1.社区规模的分布。 所有分布广泛，对于同一类别的系统类似。 数据点是模块尺寸s的对数箱内的平均值。

doi：10.1371 / journal.pone.0011976.g001

接下来，本文转向社区的拓扑结构，研究社区的链接密度及其对社区规模的依赖。子图的链接密度定义为可能链接的现有链接的分数，rho;=2t/[s(s-1)], 其中t是其内部链接的数量，其大小在节点中测量。在这里，本文使用缩放的链接密度=rho;s=2t/(s-1)，大致相当于社区节点的平均内部程度。本文选择了这个式子，因为它清楚地指出了子图的性质。 就树来说，总是有s-1个连接，因此_tree=2，另一方面，就完整的群体而言rho;=1，所以_clique=s。

图2显示了不同网络的社区大小的平均缩放链路密度。虚线表示极限情况（_tree=2，_clique=s）。能看到通信和互联网中的链路密度非常接近于下限，这意味着它们的社区是树状的，并且只包含很少的或根本没有循环。在通信网络中，缩放的链路密度不取决于社区大小，而在互联网图中，大型社区看起来更加密集。这两类中的网络是集合中最稀少的，它们平均度非常小表明它们总体上并没有比树更稠密（见表1）。一般来说，与网络的其他部分相比对社区的直观观点是“密集的”。然而，由于这里应用的方法产生了分区，树状网络的社区也必然是树状的。与上述相反，更密集的信息网络则揭示了不同的画面，社区是相当密集的对象，缩放的密度随着s的增加而增加。特别是在亚马逊网络中，slt;10的社区几乎都是群体。社交网络显示了另一种模式：模块的缩放密度随规模而定期增长，大致为幂律。社会网络中的社区远远超出两个限制性的情况：它们比树更密集，但比群体更为稀疏，除了出现更多树状的小社区之外。最后，生物网络的特点是两个制度：slt;10的社区是有树状特征的;对于较大的s值，缩放密度随s增加而增加。图3说明了每个网络类的特征社区。

图2. 社区规模的链路密度是社区规模的函数。通信和互联网由基本上是树状的社区组成，而社会和信息网络的社区更为密集。 生物网络中的小模块通常是树状的，而较大的模块更加密集。数据点是模块尺寸s的对数箱内的平均值。

doi：10.1371 / journal.pone.0011976.g002

图3.不同类网络中社区的可视化示例。 通信网络（a：电子邮件，b：Wiki Talk）包含具有星形中枢的非常稀疏的社区。 这些枢纽在社区内产生非常低的最短路径长度（见图2）。 星形集线器也存在于互联网社区（c：DIMES，d：CAIDA）中，它们相对稀疏。 CAIDA社区显示这些网络相当典型的“合并星”结构（见附录S1）。 相反，信息网络包含密集的社区，直到大型团体（e：Amazon，f：Web-BS）。 在生物网络中，社区越大，树木越少（g：黑腹果蝇，h：智人）。 最后，社交网络中的社区平均出现平均相当（i：Slashdot，j：Epinions）。

doi：10.1371 / journal.pone.0011976.g003

社区的紧凑性可以使用每个社区内的平均最短路径长度l进行测量。图 4显示了作为社区大小s的函数的l的平均值。对于所有网络，除了社交网络之外，平均最短路径长度l非常小，l lt;3。有趣的是，所有的图都显示出与网络类无关的基本模式。对于非常小的社区，l的增长的大小大约为社区大小的对数（由虚线表示），这是通常在复杂网络中观察到的“小世界”属性。本文称这些模块为微型社区。然而，对于大小为10的尺寸，l的增加突然变得不那么明显，并且几条曲线达到顶点。具有gt; 10个节点的模块是宏观社区。宏观社区中平均最短路径长度的稳定可以归因于高度节点的存在，即集线器，这使得测地线路径平均较短。本文认为，由于本文的系统大部分具有广泛的分布，所以最短的路径长度很短，但是本文观察到的骤变是意料之外的，看起来是一个全新的特征。

图4.社区内平均最短路径长度l作为社区大小的函数。经过一个初始的对数“小世界”（虚线对角线），对于sgt; 10个节点（虚线垂直线）的社区，平均最短路径增长慢得多或饱和。数据点是模块尺寸s的对数箱内的平均值。

doi：10.1371 / journal.pone.0011976.g004

就通信网络来说，对于sgt; 10并且存在l〜2的平台。这些社区是

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[140175]，资料为PDF文档或Word文档，PDF文档可免费转换为Word