剪切和摩擦角之间的关系外文翻译资料

英语原文共 36 页，剩余内容已隐藏，支付完成后下载完整资料

5.2.5剪切和摩擦角之间的关系

如前所述的剪切角phi;与切屑的形成，因此切削力的几何关系等相关理论，得到了phi;的关系是Merchant[ 60 ]和Lee and Shaffer[ 61 ]：

在beta;和gamma;是摩擦角和前角时，分别有上述的关系。

然而，实验结果得到研究者如Kobayashi和Thomson[ 62 ]和Pugh[ 63 ]适用范围广（单片）工件材料和切削条件表明，phi;以下关系更为合适

上述B和C，取决于工作的材料常数。

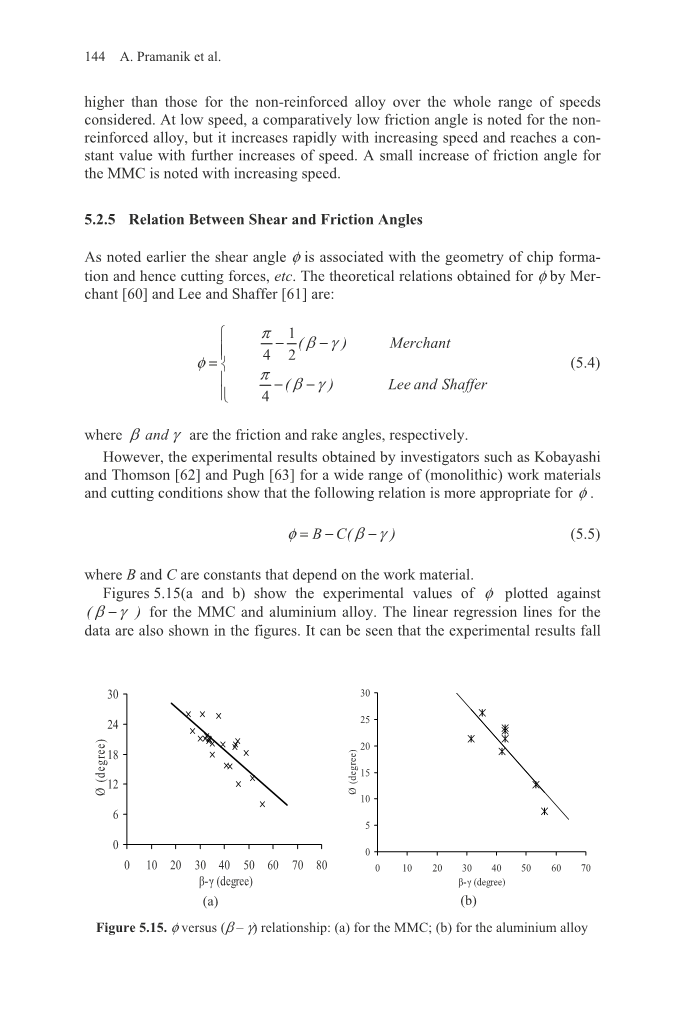
图5.15（a和b）显示出了phi;相对于测量的实验值（beta;-gamma;）对于MMC和铝合金的关系。

对于数据的线性回归线也如图所示。可以看出，实验结果的下降

图5.15phi;对（beta;-gamma;）关系：（a）对于MMC; （b）对于铝合金

分别接近由MMC和铝合金的等式（5.6）和（5.7）表示的线。

可以看出，类似于切割单片材料上面讨论的情况下，也存在phi;和（beta;–gamma;）之间的线性关系甚至对MMC也适用。在非增强合金的情况下，该关系类似于Merchant方程

（式（5.4））。显著不同的是，B的值（方程（5.5））对基体材料MMC不相同（方程（5.6）和（5.7））。

5.2.6力

在不同进料下测得的切割力和推力如图5.16所示。可以看出，对于非切削力增强铝合金稍高于MMC（图5.16（a））。对于两种材料，实验切割力随着进料的增加或多或少线性地增加并且增长率几乎相似。推力以相对切削力较低的速率增加（图5.16（b））。在较低的原始数据，推力为非增强合金高于MMC，但高于一定数值，可以看到与之前相反的趋势。 在这个阶段，可以看到两种材料的增长速率相似。推力高于较低进给时的切削力（低于0.1mm / rev），但在较高进料时观察到相反的结果。

图5.17（a，b）给出了MMC和铝合金切削力和推力随切削速度的变化。在原料为MMC的情况下，值得注意的是速度不影响两个力。对于非增强合金，这两种力都低于MMC在低切削速度的力，但随着速度的增加，力的增加，会在某一点高于MMC。随着速度的进一步增加，力开始减少（由于热软化），并在某一点再次低于MMC。在本次调查中考虑的所有切削速度的切削力高于两种材料的推力。

图5.16在进给速度为400米/分钟和深度为1毫米的切削力的变化：（a）切削力和（b）推力。

图5.17在0.1毫米/转速和切削深度为1毫米的进给速度与力的变化：（a）切削力和（b）推力。

为了研究工具-粒子相互作用对力产生的影响，对力传感器的力信号进行了研究。在切割过程中的MMC和非增强合金切削过程中的不同的切削条件的力信号如图5.18所示。这些相互作用的力信号没有显着的影响指出，信号类似于MMC和非增强合金。这可能是由于MMC之间的间距较小。据估计，对于MMC在最低切削速度（100米/分钟）的刀具将旅行距离只有0.0027秒，似乎数据采集系统不够快，以检测个别工具-粒子相互作用。与20体积%（均匀分布的球形颗粒）的加固（大小为12mu;m）间的距离是约4.5mu;m。此外，在切割深度为1毫米，由于主动切削刃的长度是超过1毫米和颗粒或多或少均匀分布在MMC，连续刀具-粒子相互作用将沿切削刃产生。因此，单独的工具-粒子相互作用的力信号的效果是不可能区分。

从这个讨论中，很明显，MMC的强度与进给和速度相比没有显着变化，在基质材料相同时。然而，MMC的强度低于基体材料，因为在变形过程中可能产生的裂缝。断屑性能的提高是由于MMC的增强颗粒的存在。在几乎所有条件下形成短切屑。纵向和横向的残余应力在基体表面的拉伸和增加由于提高的速度和进给。另一方面，存在的加固颗粒引起的压缩残余应力在加工MMC表面时会与切削刀具相互作用。MMC的表面粗糙度控制粒子的断裂和/或拔出低进给，但在较高的进给，它是由进给控制。另一方面，基体材料的表面粗糙度主要由进给控制。剪切与MMC料摩擦角的变化是类似于那些基体材料即随着进给、剪切角和摩擦角减小而增加的变化率这取决于进给。

图5.18力信号在不同的切削条件下，在加工过程中的MMC和铝合金在切割深度为1毫米：（a）进给0.025毫米/转速和速度400米/分钟；（二）进给0.4毫米/转速和速度400米/分钟；（c）速度100米/分钟和进给0.1毫米/转速；（D）速度800米/分钟和进给0.1毫米/转速。

然而，速度对剪切和摩擦角的影响是不太明显的两种材料。对于MMC，剪切和摩擦角随速度的增加非常小。另一方面，对于铝合金，最初的剪切角降低，摩擦角在低速下增加，但在一定的速度后，剪切角的增加和摩擦角保持不变，随着速度的进一步增加。phi;之间的关系（beta;–gamma;）为基体材料，即phi;= B–C（beta;–gamma;），依然保持与MMC相关。C值是1 / 2的材料和B的值分别是pi;/ 5 和pi;/ 4MMC和基体材料。

5.3模型

5.3.1力

几个模型可用于MMC材料的切削力预测。这些模型现在可以确认。Kishawy et al. [45]开发了一种基于能量的分析力模型，用于预测在低切削速度下用陶瓷刀具进行MMC正交切削时的切削力。变形的总能源消耗在初级和次级剪切带（这取决于基质材料），由于剥离/断裂能量的粒子（这取决于MMC性能）。只有在切削方向的力计算的总能量消耗加工。这种模式有几个弱点。首先，在二次变形区的能量消耗是主变形区三分之一。这种假设是基于获得的结果（单片）钢材料，可能不适用于MMCs。其次，陶瓷颗粒的裂纹宽度、初始裂纹长度和最终裂纹长度分别为1mu;m、1mu;m和颗粒周长。然而，没有证据来证明这些假设。第三，该模型只验证在低切削速度（60米/分钟），因为他们在测试中使用的是陶瓷工具。此外，还有消耗的能量没有考虑到。

Pramanik et al. [29]预测切削颗粒增强金属基复合材料的材料去除机理的基础上开发的力的力学模型。力的产生机制被认为是由于三个因素：(a)切屑形成;(b)翻动和(c)颗粒破碎/脱粘。切屑形成通过Merchant的分析，得到的芯片形成力，但由于矩阵犁变形和颗粒断裂的制定，分别与援助的滑移线场理论的可塑性和断裂的格里菲思理论。这个模型现在仍在讨论。

如前所述，在金属基复合材料的切屑形成机理的相似性，整体材料如铝或钢。应当指出的是，在加工过程中，剪切发生在一个区域，而不是在一个平面上。然而，在更高的切削速度，剪切区的厚度减小，因此它可以近似由剪切平面[ 22 ]。由于剪切平面模型的简单性和较高的切削速度时通常使用的PCD刀具加工铝基复合材料，Pramanik et al.[ 29 ]选择Merchant的分析[ 60 ]确定切屑形成的力。根据Merchant的分析，该芯片被认为是在两个相等的，相反的力的作用下作为一个单独的机构在平衡时：工具施加在晶片背面上的力，以及工件在剪切平面上对芯片基底产生的作用力（图5.19中的AB）。因此，力分量作用于刀具的方向切割，催化裂化，并在饲料的方向（推力），FTC，使用下面给出的方程[ 60 ]：

图5.19 MMC加工工艺（从Pramanik et al. [29])

在AC是剪的横截面积，tau;是MMC的剪切强度，beta;是平均摩擦角，gamma;是刀具前角和phi;是剪切角，这是由方程（5.2）得到的。剪切角，phi;，和平均摩擦角，beta;，依赖于加工条件、工件材料等因素。由于颗粒断裂被认为是单独在这个模型中，只有矩阵金属被假定为进行处理。为了确定由于金属基质犁的力分量，给出的方程[ 64 ]，这是基于使用滑移线场模型的刚性楔半空间上的滑动和正交切割。利用上述模型、力分量在切割、F_CP方向作用的工具，并确定了进给、F_TP的方向，

其中L是有效切削刃长度，RN是切削刃半径和tau;SM是基体材料的剪切强度。

注意到切削的宽度是切削刃的活动长度，它包括切削过程中切削刃的直线和圆的部分。

其中r为刀尖半径，则为进给角，F为进给量，A为切削深度。

当刀具朝切割方向移动时，带中的硬颗粒断裂或移位。因此，刀具的切削刃可以被认为是负责粒子的断裂/位移，因此会沿刀具的切削刃发生。Pramanik et al. [29]计算了MMC正交切削过程中颗粒断裂的总能量。

在正交切削中单位切边长度平均断裂能为mu;g。如果由于颗粒断裂和位移在切削力方向是F_CF，然后F_CF= E_FT =mu;_{G L}，其中L是切割距离。F_CF被下列公式决定

为了确定由于在推力方向上的颗粒断裂/位移的力，合力的方向必须确定。据推测，加固颗粒均匀分布和均匀的平均直径的球形，和颗粒与切削刃的相互作用可以表示为一个粒子放置在处理区的中间，如图5.20所示。忽略了摩擦过程中的相互作用，合力的方向是由下列关系决定的

在delta;从切削方向测量合力的角度，DP是粒子和H的平均直径的耕作区的宽度，这是由

然后，由于粒子的断裂和位移推力方向的力的组成部分是

力F_CF和F_TF可以由上述方程时mu;_G是已知的。因此，在切削力和推力方向F_CF和F_TF作用于刀具上的总作用力

图5.20颗粒与切削刃的相互作用从（Pramanik et al. [29])

为了确定使用粒子方程（5.11）-（（5.15））所引起的粒子断裂和位移的力，需要mu;_g的值。为了确定mu;_g，采用了以下方法。值得注意的是，严和张[ 65 ]计算颗粒断裂比能在基复合材料铝合金上使用。在[ 66 ]Griffith的公式用于估计一个棱锥压头下颗粒断裂的能量。确定的粒子能量的具体能量减去相应的铝基体材料的划痕能量的复合材料与SiC（10和20重量%）和Al2O3（和20重量%）的颗粒增强的总的比能量。Pramanik et al. [29]使用[ 65 ]中的结果来确定mu;g，因为在导出方程（5.11）中，刀具边缘被认为是粒子破裂的原因。

对于给定的槽深H，特定粒子的断裂能mu;f可以从给出的结果[ 65 ]。划痕的粒子断裂E_F总能量为

其中一个是槽的横截面积，theta;相反的面孔和L之间的压头顶角是划痕的长度。注意移除的物料体积是AL = h2 tantheta; L。有效压头边缘长度引起颗粒断裂

因此，每单位切削刃长度L_ei的粒子断裂的能量是

mu;_g的值是从一个范围内的数据[ 65 ]中，得到的值mu;_g为0.01焦耳/毫米的SiC（20体积%）。使用给定的数据和方程（5.11）-（5.15），切削力和推力分量，由于颗粒的断裂和位移，可以确定不同的切削条件。

首先确定了切屑形成、犁削和颗粒断裂和位移的预测力。这些力，然后总结确定总的力量在切割和推力方向（方程（5.16）），并与实验力相同条件下进行比较此外，在相同的条件下，切削力使用模型的kishawy等人描述的计算。[ 45 ]。预测从这个模型与 Pramanik et al. [29]的模型和实验结果给出了图5.21 - 5.23。基于[ 66 ]中的信息，SiC的最大拉应力为245兆帕。图5.21比较预测和实验力量与不同的饲料。在这个图中，实验力的结果表示由符号和由线的预测结果。实线表示使用模型在[ 29 ]的预测，而虚线代表那些获得使用能源为基础的模型[ 45 ]。正如预期的那样，实验的切削力和推力可以看出与进给量的增加近似线性增加。

图5.21不同进给量的预测力与实验力的比较（从Pramanik et al. [29]）

切削力的增加率高于推力。预测结果从模型[ 29 ]表现出相同的趋势与实验的优秀定量协议。另一方面，在[ 45 ]中的模型可以看出低估切削力相当。

预测和实验的力的结果与不同深度的切割之间的比较，如图5.22所示。类似于图5.21所示的力的变化，实验和预测的力结果与切削深度近似线性增加再次，一个更大的切削力比推力以及优良的定性和定量的协议之间的预测增长率（从Pramaniket al.[ 29 ]和实验结果已获得。然而，该模型在[ 45 ]低估了切削力在测试范围内的深度。预测和实验结果的不同切削速度的力之间的比较，如图5.23所示。与上面所讨论的进给力和深度的变化不同，在这种情况下，切削力和推力可以随速度的增加呈近似线性下降，并且有类似的下降率。再次，优秀的定性和定量预测之间的协议（从Pramanik et al. [29]的模型）并且实验结果似乎存在。另一方面，从能量为基础的模型[ 45 ]的预测不受切削速度（因此水平线）和测得的切削力高于所有速度的预测。

图5.22。不同切削深度的预测力与试验力的比较（从Pramanik et al. [29]）

图5.23。不同切削速度下预测力与实验力的比较（从Pramanik et al. [29]）

从上述预测（从模型[ 29 ] ]和[ [ 45 ] ]和实验结果之间的比较，很显然，从模型中的预测[ 29 ]表现出优异的定量/定性与实验结果一致。然而，该模型在[ 45 ]可以看出低估预测切削力相当。这种低估可能是由于只有基质合金的估计时，由于在第一和第二剪切区的塑性变形的特定能量的考虑。考虑

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[141977]，资料为PDF文档或Word文档，PDF文档可免费转换为Word