英语原文共 7 页,剩余内容已隐藏,支付完成后下载完整资料
一种基于Tent混沌映射的图像加密方法
李春虎·罗光春·柯勤·李春宝
收到日期:2014年11月25日/接受日期:2016年8月16日copy;斯普林格科学 商业媒体2016年德雷赫特
摘要
图像加密近年来一直是一个有吸引力的研究领域。基于混沌的密码图形算法提出了一些新的有效方法来开发安全的图像加密技术。本文提出了一种基于混沌帐篷图的新型图像加密方案。基于这种地图的图像加密系统显示出一些更好的性能。首先,对混沌帐篷地图进行修改,生成更适合图像加密的混沌密钥流。其次,基于混沌的密钥流由一维混沌帐篷地图生成,在随机性和安全性方面具有较好的性能。所提出的图像加密方案的性能和安全性分析使用众所周知的方式来执行。失败分析的结果令人振奋,可以得出结论,该方案是有效和安全的。
关键字:Tent混沌映射,混沌密码学,图像加密
1介绍
20世纪70年代,混沌理论已经建立,并已用于许多不同的研究领域,如物理学,数学,工程学,生物学[1,2]。自从Matthews引入第一种基于混沌的图像加密方案[3]以来,已有文献提出了许多利用混沌映射的基于混沌的数字图像加密方案[2,4,16]。近年来,混沌加密一直是一个有吸引力的研究领域。实现混沌映射在密码系统开发中的吸引力在于混沌映射的特点是:(a)对其初始条件和控制参数的高度敏感性;(b)其轨道发射的不可预测性;(c)实现硬件和软件的简单性,从而实现高加密速率。这些特征可以与一些非常重要的密码属性相联系,如混淆和扩散,平衡和雪崩特性[17]。在过去的二十年中,研究人员提出了许多图像加密方案[18,19]。二维混沌catmap被推广到3D来设计一个实时安全的对称加密方案[20]。
毛等人[21]提出了一种基于三维混沌贝克映射的快速图像加密方案。Pareek等人[22]使用两个80位外部密钥的混沌逻辑映射。任何其他的选择(伯努利,负伯努利和谷地图)[23-25]将导致完全相同的属性地图。
在本文中,我们深入分析了一个混乱的帐篷地图。考虑混沌系统的性质,提出一种基于混沌帐篷映射的新型图像加密方案。这项工作是我们第一次尝试,以探索混沌帐篷地图作为密码系统。该算法利用了高复杂度的混沌映射。由这种类型的地图生成的序列的随机性非常高。同样在这个算法中,映射的初始条件和参数在加密期间被修改(因为它们连接到明文和密文),并且该映射对初始条件的非常小的变化的高度敏感性和控制参数提供了非常安全的加密算法。
本文的结构如下。第二节介绍混沌帐篷地图及其属性;第三节提出了我们的算法的细节(包括加密和解密);实验结果在第四部分中介绍。安全讨论的细节显示在第五部分。
最后,结论在第六部分中得出。
2 Tnet混沌映射
Yoshida[27]等人研究了Tent映射的混沌行为(一个分段线性,连续映射的唯一极大)在其混沌区域内的不变密度和功率谱分析。随着最大高度的降低,在混沌区域中发生连续的带分裂跃迁,并积累到过渡点进入非混沌区域。帐篷映射是拓扑共轭的,因此地图的行为在这个意义上在迭代中是等价的。混沌帐篷映射[27 通过一下公式得出:
(1)
(2)
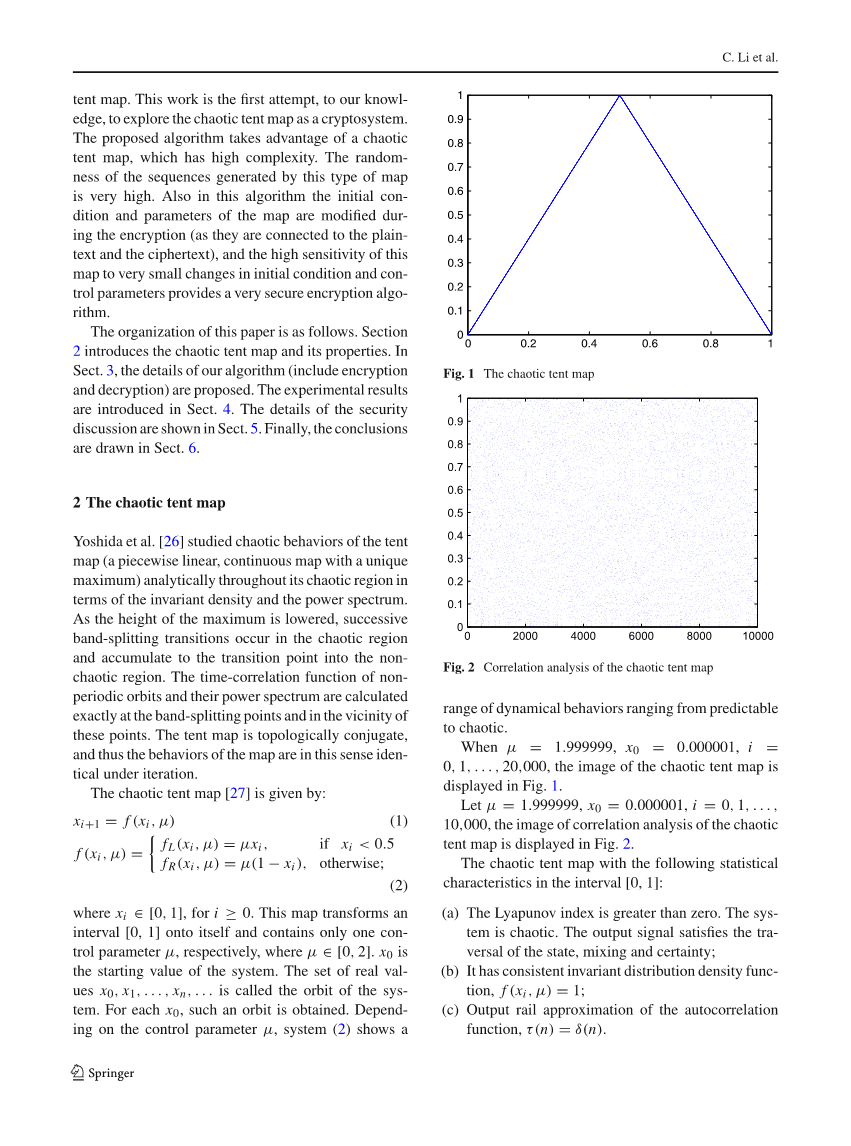
当,且。当,是公式的起始值,该映射将区间[0, 1 ]转化为自身,仅包含一个控制参数。实值集被称为系统的轨道,对于每个,得到这样的轨道。根据控制参数,公式(3)展示出了从预测到混沌的一系列动态行为。当=1.999999时,=0.000001,i=0, 1,hellip;20000,在图2.2中显示了混沌帐篷映射的图像。设=1.999999,=0.000001,i=0, 1,。hellip;10000,在图2.3中显示了混沌映射的相关分析。混沌帐篷映射区间(0, 1)中具有下列统计特征:
- 李雅普诺夫指数大于零。这个公式是混乱的。输出信号满足状态是混合和确定性;
- 具有一致的不变分布密度函数,;
- 自相关函数的输出轨近似,。
图1 Tent混沌映射
图2 混沌映射的相关分析
利用该映射生成的混沌序列具有良好的统计特性,但在n维预处理下,则表现出一定的周期性。随着值的增大,混沌序列呈现周期性。但随着值的变小,混沌序列表现出很强的随机性,但在迭代后,混沌序列的输出值为零。 这是因为:利用分段线性函数产生混沌映射,初始值的精度总是有限的,由于计算机精度的限制,接近1的近似数将更可能被处理为1。因此,mu;的值接近2。在混沌区域,帐篷映射具有独特的遍历不变测度是相对于勒贝格测度的绝对连续。
3提出的算法
3.1图像加密算法
在本节中,我们使用混沌帐篷地图Eq.(2)执行加密过程。本文提出的图像加密算法由以下主要步骤组成:
(1)读取普通图像(原始图像)(Matimes;b),得到M,例如用[a,b,c]来保存M的大小,a = 256,b = 256,c = 3,设N = a * b * c,并启动混沌映射的控制参数(mu;)
(2)将秘密(加密)密钥x0输入到算法中。使用系统(2)迭代混沌映射图N次,得到关键数组x(n),x(n)的大小为N;
(3)使用关键矩阵x(n)对矩阵(Matimes;b)中的每个元素进行加密,即将原始图像(Matimes;b)分量与矩阵x(n)混合;
(4)步骤(3)的结果图像是加密图像。
图像加密方案如图3所示。
图3加密算法的流程图
3.2图像解密算法
在本节中,我们使用混沌帐篷映射来实现解密过程。本文提出的图像解密算法主要包括以下步骤:
(1)读取加密图像(加密图像)(Matimes;b),得到M的大小,例如用[a,b,c]来保存M的大小,a = 256,b = 256,c = 3, N = a * b * 3,并初始化控制参数(mu;),控制参数(mu;)必须与加密方案的步骤(1)相同。
(2)将密钥(解密)x0输入到算法中,密钥x0必须与加密密钥相同,否则我们不会得到原始图像。用系统(2)迭代混沌帐篷地图N次,得到关键数组x(n); x(n)的大小是N;
(3)利用关键矩阵x(n)对矩阵(Matimes;b)中的每个元素进行解密,即利用关键矩阵x(n)从加密图像(Matimes;b)分量中提取出原始图像。
(4)步骤(3)的获得图像是解密(原始)图像。
图像解密方案如图4所示。
图4解密算法的流程图
4实验结果
下面的实验结果被用来证明所提出的图像加密算法的有效性。标准灰度图像Lenna(图5a)的大小为256times;256像素用于本实验。加密结果如图5b所示。从图中可以看出,在相应的密文中没有可见或可见的图案。图5c给出了解密的结果。从图中可以看出,与原始图像没有区别。图5f表示使用错误密钥解密的结果。从图中可以看出,在相应的加密图像中没有可见的图案或阴影。
图5 a原始图像,b加密的图像,c解密的图像,d原始图像的直方图,e加密图像的直方图,f使用错误键解密的图像
5安全分析
5.1密钥空间
对于每个密码系统而言,密钥空间是非常重要的。密钥空间必须足够大才能进行蛮力攻击。在我们提出的方案中,图像解密的密钥空间由以下公式计算:
T(x0,mu;)=theta;(x0times;mu;),
其中x0isin;[0,1],mu;isin;[0,2],x0和mu;的每个精度为10-16,即密钥空间的大小为2106((1016)2)。这个密钥空间对于暴力攻击来说足够大[28]。在这个方案中,我们把关键原理设为:x0 = 0.000001,mu;= 1.999999。当选密钥时,错误密钥和正确密钥的区别是。例如,使用x0 = 0.0000009999999999作为解密加密图像的错误密钥,我们得到了图5f中显示的错误解密图像。
5.2密文的分配
图像直方图通过绘制图像的数量来显示图像中的像素是如何分布的。这里将Lenna图像作为原始图像,其大小为(256times;256)。原始图像的直方图和相应的加密图像如图5d所示。当显示原始图像和加密图像的直方图时,它没有提供任何线索来对加密图像使用任何统计分析攻击[29]。
表1模拟原始和加密图像中两个相邻像素的相关系数
5.3两个相邻像素的相关性分析
通过对加密图像中相邻像素之间相关性的测试显示了出众的混淆和扩散特性[30]。我们还分析了“Lenna”加密图像中相邻像素之间的相关性。我们使用了Eq.2来计算水平,垂直和对角线上的相关系数,并且已经使用了以下关系[31]:
其中和是图像中相邻像素的值,N是从图像中选择用于计算的像素的总数。我们在原始图像和加密图像中分别选择了1000个图像像素,分别计算相邻像素在对角线,水平和垂直方向上的相关系数(表1)。它证明了加密算法已经覆盖了原始图像的所有字符,显示出平衡0:1比例的良好性能。加密图像和解密图像的相关性如图6和图7所示。
图6原始图像的相关性分析
图7加密图像的相关性分析
5.4信息熵
信息理论是Shannon于1949年创立的数学理论[2,32]。现代信息理论涉及纠错,数据压缩,密码学,通信系统和相关主题[2]。有一个众所周知的计算这个熵的公式:
其中P(si)表示符号si的概率,并且熵以位表示。加密图像的理想熵值应为8。加密图像的熵计算(图5b)如下:
结果表明,加密图像的熵与理想熵值非常接近,比其他现有算法的熵高8个数量级。这表明所提出的图像加密算法的信息泄漏率接近于零。
5.5速度分析
除了安全考虑之外,算法的运行速度也是一个好的加密算法的重要方面。我们通过使用所提出的图像加密方案来测量不同尺寸的几种彩色图像的加密/解密速率。时间分析已经在使用Matlab的Debian 7.5上运行的核心2 Duo 2.26 GzCPU和4 GB RAM笔记本上完成。表2列出了该算法对不同大小图像的平均加密/解密时间。
表2几个不同大小的图像的平均加密时间
六,结论
在本文中,我们集中在图像加密领域。加密和解密方案得到了支持,进行了实验和安全分析。
致谢 四川省科技厅基金资助项目号:2013JQ0005,2014JY0010。
参考文献
1. Behnia,S.,Akhavan,A.,Akhshani,A.,Samsudin,A .:基于雅可比椭圆映射的图像加密。 J. Syst.Softw。 86(9),2429-2438(2013)
2.Akhshani,A.,Akhavan,A.,Lim,S.-C.,Hassan,Z .: Animage encryption scheme based on quantum logistic map.Commun。非线性科学。 NUMER。模拟料。 17(12),4653-4661(2012)
3. Matthews,R.A .:遗传算法在隐秘分析中的应用。 Cryptologia 17(2),187-201(1993)
4. Ye,R.,Guo,W .:一种基于混沌的图像加密方案,采用多模态偏斜帐篷图。 J. Emerg。 Trends Comput.Inf。科学。 4(10),(2013)
5. Ye,R.,Zhou W:一种基于混沌的图像加密方案,采用三维倾斜帐篷图和耦合图格。诠释。 J.Comput。网络。天道酬勤。 SECUR。 4(1),25-28(2012)
6. Kanso,答:自我缩小的混沌流密码。 Commun.Nonlinear Sci。 NUMER。模拟料。 16(2),822-836(2011)
7.Akhavan,A.,Samsudin,A.,Akhshani,A .:基于非线性混沌映射组合的对称图像加密方案。 J. Frankl。研究所。 348(8),1797-1813(2011)
8. Jakimoski,G.,Kocarev,L.,et al .: Chaos and cryptogra-phy:block encryption ciphers based on chaotic maps。 IEEETrans。电路系统。我Fundam。理论应用48(2),163-169(2001)
9.张,L。,L。,X.,王,X.:一种基于混沌映射的图像加密方法。 Chaos Solitons Fractals24(3),759-765(2005)
10. Zhang,W.,Wong,K.-W.,Yu,H.,Zhu,Z.-L .:使用反向二维混沌mapand依赖扩散的图像加密方案。 COMMUN。非线性科学。 Numer.Simul。 18(8),2066-2080(2013)
11. Alvarez,G.,Li,S .:混沌密码系统的一些基本密码要求。诠释。 J. Bifurc。 Chaos 16(08),2129-2151(2006)
12. El-Latif,A.A.A.,Li,L.,Wang,N.,Han,Q.,Niu,X .:基于量子混沌系统的混沌图像加密新方法,利用颜色空间。 Signal Process.93(11),2986-3000(2013)
13. Fridrich,J .:基于二维混沌映射的对称密码。诠释。 J. Bifurc。 Chaos 8(06),1259-1284(1998)
14. Lian,S.,Sun,J.,Wang,Z .:基于合适的混沌标准映射使用的分组密码。 Chaos Solitons Fractals26(1),117-129(
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[23348],资料为PDF文档或Word文档,PDF文档可免费转换为Word
课题毕业论文、外文翻译、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。