沙漠地区的微波发射和散射：理论计算与卫星测量的对比外文翻译资料

英语原文共 15 页，剩余内容已隐藏，支付完成后下载完整资料

沙漠地区的微波发射和散射：理论计算与卫星测量的对比

摘要：沙漠地区地表的发射和散射通过利用SSM/I和AMSU微波卫星仪器的模拟和测量来分析。沙漠几乎是没有植被覆盖的，所以卫星辐射计能够观测到不同矿物的发射率，比如石灰岩和石英。此外，因为沙漠含有很少的水分，热量发射源于地表以下许多波长的深度。在高频状态下，这种情况下辐射的穿透深度是最小的，辐射测量值显示出了表面温度很大的日变化，日变化大约在下午1点达到它的最大值。相反地，在低频状态下，这时穿透深度是最大的，辐射测量值显示出了地下表面温度小的日变化，日变化大约在上午6点达到最小值。除了这些发射信号，砂粒也会散射微波辐射。尽管和其他散射介质相比（积雪和降水），更大的吸收和砂粒的体积分数（即硬度）减少散射，大量的散射仍然使得测量值随着频率的升高而减小；虽然散射的影响很小，但是介于19至85GHz之间的SSM/I测量值显示沙漠散射上升流区的微波辐射的方式近似于弱降水的方式，这使得在干旱地区唯一地识别出降水十分困难。有趣的是，更高频率时AMSU在沙漠地区的测量值，在150GHz时几乎和89GHz时相同，而对降水的测量值在150GHz时远比89GHz时小。在高频状态下这些不同的光谱特征能够提供区分沙漠地表散射和降水散射的方法。

关键词：重介质应用，沙漠散射，发射，沙漠微波特性，微波遥感

Ⅰ.引言

本文进行了关于沙漠地表微波辐射特性的分析研究。砂粒是已通过各种物理/化学过程退化的基本岩石。砂粒的组成成分根据当地的岩石来源和环境而不同，最常见的组成部分是二氧化硅，通常形成石英。纯石英晶体（单一晶体）的密度大约是2.65，而砂粒的密度大约在1.4-2之间变化，所以砂粒的体积分数或者硬度在0.53和0.75之间。此外，根据美国农业部对土壤质地的定义，砂粒的直径从细沙的0.05mm变化至粗砂的2mm。因为砂粒能够有毫米大小的直径并且其体积分数小于整体，因此它们能够散射并且吸收高频微波辐射。这些参数都列在表Ⅰ（a）中作为参考。

尽管我们很了解砂粒的矿物学知识和尺寸，但是我们不了解它的辐射吸收特性。表Ⅰ（b）列出了最常见的四种沙漠材料成分的介电常数的实际部分和折射率成分。正如表中所展示的，介电常数从石灰石的最大值，大约是7.5变化至石英的最小值3.0，这和雪的介电常数很相近（例如[4]，[10]和[16]）。搭载在美国宇航局Nimbus-5和Nimbus-6号卫星上的电子扫描微波辐射计通过19和37GHz通道首次观测到了不同的矿物[1]。这两个传感器都用于从亮度温度测量的空间变化中识别出沙特阿拉伯地区的石灰石和石英，即表面发射率高的是石英，低的是石灰石。最近，Prigent et al研究了碳酸盐岩石例如石灰石的低微波发射率[15]。其他的研究也测量了砂粒的介电常数[9]和辐射穿透深度[2]，[14]，在这些研究中固体介质的，其中是介电常数的虚部，是自由空间的波长。

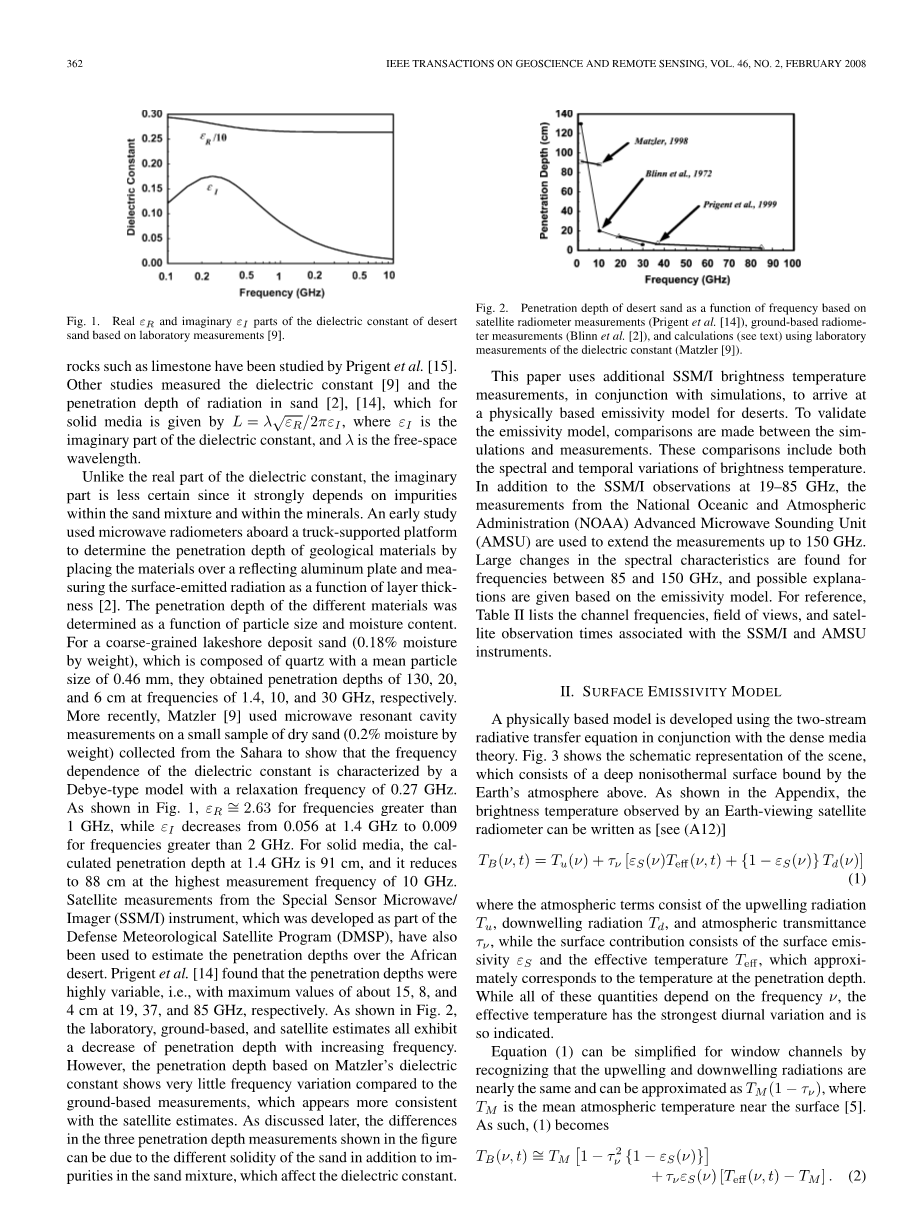
介电常数的虚部和实部不一样，虚部更不确定因为它取决于砂粒混合物内部和矿物内部的杂质。一项很早的研究使用装载在卡车平台上的微波辐射计来确定地质材料的穿透深度，他们把材料放置在一个反射铝盘上，然后测量表面发射辐射作为层厚度的一个函数[2]。不同材料的穿透厚度由粒子尺度和水分含量的一个函数确定。由平均粒子尺寸为0.46mm的石英构成的粗粒度的湖岸沉积砂（按重量计算含0.18%的水分）的穿透深度在1.4,10和30GHz频率下分别为130,20和6cm。最近，Matzler[9]利用微波谐振腔测量了一小块取样自撒哈拉沙漠的干沙样品（按重量计算含0.2%的水分），该测量表明了介电常数和频率的关系可以通过弛豫频率为0.27GHz的德拜型模型来表征。正如图1所展示，时频率大于1GHz，同时从频率为1.4GHz时的0.056减小到频率大于2GHz时的0.009。对于固体介质，1.4GHz时计算所得的穿透深度是91cm,并且它在最高测量频率10GHz时减小到88cm。作为国防气象卫星计划发展的一部分，SSM/I仪器上的卫星观测也被用来估算非洲沙漠的穿透深度。Prigent et al[14]发现穿透深度具有高度可变性，即在19,37和85GHz时最大值分别约为15,8和4cm。正如图2所示，实验室估算，地基估算和卫星估算都证明了穿透深度随着频率的增大而减小。然而，基于Matzler介电常数的穿透深度与地基测量值相比显示出很小的频率可变性，它和卫星估算相比也变现得更具连续性。正如后面所讨论的，图中展示的这三种穿透深度测量方法的差异是由于砂粒不同的硬度和砂粒混合物中的杂质引起的，因为这些差异会影响介电常数。

本文另外还使用SSM/I亮温测量值结合模拟来构建一个物理基础的沙漠发射率模型。我们将通过对比模拟值和测量值来验证发射率模型。这些对比包括两者亮温的光谱和时间的变化。除了在19-85GHz内的SSM/I观测值，来自NOAA的AMSU测量值用来拓展测量值至150GHz。在85到150GHz的频率内，光谱特性有很大的变化，基于发射率模型我们可以给出一些解释。表Ⅱ列出了一些通道频率，视场角和有关SSM/I和AMSU仪器的卫星观测时间供参考。

Ⅱ.表面发射率模型

该物理基础模型建立在辐射传输二流模式基础以及致密介质理论上。图3展示了现场示意图，它由包裹在地球大气上面的一个深非等温面组成。如附录中所示，通过地球观测卫星辐射计观测得到的亮温为[见（A12）]

（1）

该式中大气术语包括上行亮温，下行亮温和大气透过率，以及表面贡献量包括表面发射率和有效温度，有效温度大致对应于穿透深度的温度。所有这些量都取决于频率，同时有效温度具有最强的日变化性。

等式（1）在大气窗区可化简，这时的上行和下行亮温接近不变，可用近似计算，是接近地表的平均大气温度[5]。这样的话，（1）式就化为

（2）

在（1）和（2）式所有的参数中，发射率最难计算。一种相对简单的方法就是把沙漠表面当作无限深，并且是由低损耗，具有相同的几何形状和介电常数的砂粒（即不含水分）组成的。这时发射率和均匀等温面上的相同[21]，它可以简单地写作[见（A13）]

（3a）

其中

（3b）

等式（3a）把表面界面和地下表面体积特性结合成单一表达式。在（3a）中的首项，即，是在大气/地表交界面的反射率，其中是折射地表面下形成的上行辐射的反射率。这个反射率也反射入射到地表的下行大气辐射。对于光滑的地表，反射率由菲涅耳等式中的介电常数，视角和极化作为输入参数来确定。表Ⅰ（b）展示了针对不同矿物计算得到的透过率。正如后面所展示的，透过率占了卫星辐射计观测所得亮温（即发射率）的区域差异的很大比重。实际上，通常我们直接把透过率等同于许多无雪地表的发射率。然而，（3a）中的第二个括号项引起了体积散射，这在高频段非常重要。它包括了由（3b）定义的相似参数a，a是单粒子反照率（散射与消光系数之比）和不对称参数g（前负散射能量除以2）的函数。这两个量在附录中有定义，而且都取决于介电常数，体积分数，砂粒尺度和微波频率。模拟值将和卫星测量值进行对比，对比表明砂粒体积分数在0.5和0.7之间时其虚部对应的介电常数是0.11和0.06。当平均介电常数为，体积分数为0.6时，图4（上面的）展示了SSM/I视角为53.1°时垂直极化发射率作为频率的函数，其中每一部分都针对不同粒子半径（0.3和0.5mm）。需要注意到体积散射会使得发射率随着频率和粒子半径的增大而减小。除了发射率，图4（下面的）展示了对应的穿透深度，它基本上和粒子半径没有关系。

亮温（2）也包含了介质的有效温度，它取决于地表下温度廓线和辐射穿透深度。温度廓线的精确表示能够通过热量传输1-D等式获得，该等式的通解为

（4）

使用第一项级数展开，温度为

（5）

其中 ，，是地表温度最大值，出现在时刻，是地表温度最小值，它出现在12小时之后。等式（5）也包含标高h，它定义了温度随高度减小的比率。表Ⅲ列出了从热扩散系数计算得到的不同材料的标高[12]。对于沙漠砂粒，标高大约是8cm。温度的日变化取决于（5）中的余弦项所得的太阳能加热项，它包含了地球自转频率（ ）。举例来说，图5比较了（5）中列出的地表温度日变化和实际的撒哈拉沙漠中心的测量值（[13]；以及[12，p.82]）。图中所示的系数，和是通过将地表温度测量值的时间序列拟合为傅立叶级数得到的。图5也展示了使用（4）中第一、第二次谐波分量得到的改进拟合值，其中系数，，，和是重新由傅里叶分析确定的。然而，为了简化亮温模型，只有使用（5）中给出的附录里的第一次谐波分量来求得有效温度[见（A11c）]

， （6a）

并且

（6b）

其中

（6c）

如图3所示，系数和是b参数的函数，该函数取决于穿透深度L与温度标高h的比率以及发射角的cos值（）。如附录所示，对于固体介质，反照率是零所以a=1,且吸收系数是，其中是自由空间波长。然后穿透深度就减小至已知结果。然而，总的来说，对于颗粒状的介质，穿透深度也由体积分数和粒子半径决定。使用致密介质理论[19，p.498]中的有效介电常数，它引起了相干波互相作用，这时的穿透深度总体上是粒子半径，体积分数和粒子介电常数的函数。然而，针对与沙漠砂粒相关的参数的变动（,,），穿透深度大概可以表示为

（7）

其中图6（上面）比较了这个方程和精确的模型计算。关于一对一直线的散射主要取决于粒子半径，这在（7）中被省略了因为它主要在高频状态时才重要，那时穿透深度很小。注意对密集的粒子（即），方程结果减小至固体介质算得的值。第Ⅰ部分中提到以及在下一部分描述的穿透深度的SSM/I估算值结合（7）能够得到将介电常数虚部与体积分数相关联的方程。图6展示了每一个SSM/I频率的双曲线关系（下面）并且后面将基于模拟和SSM/I测量的对比来估算介电常数和体积分数。

当时方程（6a）能够简化，因为，，并且，所以大约是在穿透深度处的温度。这种简化方法主要应用在高频区域，因为这时穿透深度远小于标高且。然而，总的来说，当且地表温度为最大或最小值时，和的差异是4.5K。研究还发现当把等于时，基于（5）和（6）的穿透深度差异会升至5cm。不过，正如接下来所讨论的，近似值被用来从SSM/I测量中估算穿透深度。

Ⅲ.SSM/I发射测量

在[14]中，通过（4）中由前两次谐波首先表示温度廓线推导了北非和沙特阿拉伯地区SSM/I频率（19,37和85GHz）下的穿透深度和发射率。在图5的情况下，通过地表温度（通过红外卫星测量每天得到八个时次的值）的傅里叶分析得到系数（，，，和）。通过修正热扩散系数至（即）和假设（1）中，在每一个SSM/I频率，SSM/I每天的亮温测量值都被用来估算穿透深度和发射率。此外，也需要用到（1）中的大气项，它是使用数值天气分析模型中的大气温度和水蒸气获得的。注意推导的穿透深度不需要任何关于发射率或者穿透深度模型的假设。然而，计算出的穿透深度在不同的沙漠地区变化相当大，这可能是因为砂粒具有不同的介电特性，体积分数或硬度。在所有的频率段，最小值接近于零，而最大穿透值在85,37和19GHz时分别为4,8和15cm。既然在19和37GHz时的穿透深度比7.5cm的标高大，假设在两个低频段就不那么精确了。然而，Prigent et al[14]所作的合成穿透深度和发射率地图是合理的。此外，正如图4所示（下面），当介电常数为，体积分数为0.6时SSM/I最大穿透深度和模型计算值一致。正如下一部分所讨论的，这些选中的参数也和其他独立的SSM/I测量值相一致。

除了有效温度的贡献外，亮温还取决于发射率项。正如以前提到的，（3a）中的首项（1-RS）得到了表Ⅰ中列出的透射率。为了展示更细致的描述，图7（下面左边）展示了在SSM/I视角为53.1°时作天底观测的作为介电常数实部函数的发射率。这张图也基于它们的介电常数识别了表Ⅰ中列出的不同地表面。注意石英和砂石的发射率接近于总体值，而石灰石在垂直极化时具有最低的发射率。作为这些地表特征的一个例子，图7（上面）展示了1996年7月北非和沙特阿拉伯地区37GHz时月平均SSM/I垂直极化亮温测量值。此外，图7还展示了从美国地质调查/美国石油公司得到的阿拉伯半岛1963年的地质图（下面右边），该图勾画出了包含大量石灰石沉淀的区域。观察最低的SSM/I亮温（）是否与地质图中的石灰石沉淀区契合。尤其要注意在沙特阿拉伯中部石灰石沉淀区分别显示在SSM/I测量值和地质图上的新月状的特征。这个相同的特征由Allison[1]使用早期的微波传感器（搭载在Nimbus-5和Nimbus-6号卫星上的ESMR）发现。由Prigent et al[15]使用19GHz时SSM/I垂直极化测量值而绘制的发射率地图也展示了相同的地表特点。通过这些对比，表明了沙漠地区亮温变化的一部分原因在于发射率变化而不是地表温度变化。

有趣的是，在微波频率段的相同地表特征的空间变化也能在IR波段观察到[1]。比如一个最近的例子，图8展示了最新的发射率图像，它使用了搭载在美国航空航天局发射的地球观测系统卫星上的中分辨率成像光谱仪（MODIS）波段的测量值[11]。有关分子辐射吸收的物理机制在微波频段（即转动模态）和IR频段（即振动模式）很不一样。同样地，石英和砂石的发射率在微波频段接近总体值但是在IR频段发射率很小（0.7）。另外，石灰石的微波发射率和其他沙漠矿物相比很低，但是和IR频段总体发射率很接近。

图7中的高亮温区域归因于表Ⅰ中的高发射率地表，即含石英和砂石的地区。然而，除了有IR图像支持，这些高发射率区域也可以使用19和22GHzSSM/I垂直极化通道来验证。地表发射率在这些接近的通道几乎相同，所以主要

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[31449]，资料为PDF文档或Word文档，PDF文档可免费转换为Word