行星波的准谐振振幅与近期北半球极端天气外文翻译资料

英语原文共 12 页，剩余内容已隐藏，支付完成后下载完整资料

行星波的准谐振振幅与近期北半球极端天气

Vladimir Petoukhov^a,1,Stefan Rahmstorf^a,Stefan Petri^a,and Hans JoachimSchellnhuber^a,b,1

^aPotsdam Institute for Climate Impact Research,D-14412 Postdam,Germany;and ^bSanta Fe Institute,Santa Fe,NM 87501

Contributed by Hans Joachim Schellnhuber,January 16,2013(sent for review June 15,2012)

近几年来，北半球遭受了严重的局地夏季极端天气的影响，比如说2003年的欧洲高温波动，2010年的俄罗斯高温波动和巴基斯坦印度西北部的河流爆发的洪水，还有2011年美国的高温波动。这里，我们提出一个常见的在北半球中纬度地区产生持久的大气环流纵向行星尺度高振幅模式的机制。这种模式假设纬向波数为6，7或8，这正是上述极端天气的特征。我们发现，这些模式可能是由于受到具有纬向波数kasymp;m的自由天气波的中纬度波导的不利影响。通常来说，上述波数m对气候平均热力作用和地形强迫的四维动力响应较弱。然而，准线性条件可能有利于这种中纬度波导放大这种反应。

大气动力学|中纬度罗斯贝波问题

2003年的夏天在北半球非常特殊。（1-4）它的显著特征是在欧洲持续的闭合环流模式。（1-4）反常高温天气支配了欧洲大部分地区的夏季的大部分时间，瑞士、法国西北部和德国南部都达到了最高温度异常。Schar和同事们*2004（3）提出，他们观测到的气候变暖趋势（i）将夏季温度的概率分布转向温度更高的值（ii）扩大了这种概率分布，使得极端天气的发生变得更有可能，这有可能是由温度和土壤干燥度之间的正反馈引起的。我们注意到，由于全球变暖导致的概率分布的转变和扩大几乎肯定会引起极端暖季事件发生频率的显著增加。（5-7）然而，即使是在数据中发现的变暖趋势被充分考虑进去，并且假设均方差增加50%，2003年夏季高温波动的极端温度和持续时间仍然不太可能。比如说，Luterbacher等人为欧洲地区估计了一百年的回归期。（2）同时，近年来已发生的其他几个强烈的局地异常夏季天气已经使人们怀疑只有纯粹的极端机制才能起到作用。全球观测证明，这些极端情况，比如说2010年的俄罗斯高温波动和美国2011年创纪录的高温波动，几乎持续了整个夏天——这不是常见的闭合环流固有的，具有约5-7天的特征性e折时间——这实际上是半球尺度：整个北半球包含着一个稳定的大气环流异常模式。（4,9-14）

在此，基于每日国家环境预测中心（NCEP-NCAR）的再分析数据，我们强调在上述地区夏季极端天气下的北半球中纬度近似稳定的经向速度的特征是不规则的高振幅波动模式，其中纬向波数m=6，7或8.后者可能是由于在中纬度波导内具有纬向波数kasymp;m的准静态自由波，导致上述波数m的准振谐扩张，就像第Ⅰ部分和第Ⅱ部分所说的。

Ⅰ.准共振假设

一般来说，大规模的中纬度大气环流具有特征（i）区域波数kge;6的自由天气尺度罗斯贝波主要沿纵向传播，相速度casymp;6-12米/秒（ii）准静止行星尺度罗斯贝波，其中casymp;0，频率omega;asymp;0并把各种纬向波数m作为大气环流对准静态（例如气候平均值），空间不均匀的非绝热源/汇和地形的对应。（16-28）具有kasymp;6-8的中纬度自由天气尺度的准静态分量通常很弱，经向速度的大小小于1.5-2米/秒。（26，27）下面，k和m分别表示自由天气波和上面提到的准静止行星尺度罗斯贝波的纬向波数。我们的假设是，在考虑到的夏季极端天气事件中，某些持续的高振幅波结构在大规模中纬度大气经向速度（以下称为V）的场中演化，其中自由天气波的准静止部分kasymp;6-8作出了特别大的贡献。这些结构可能来自中纬度纬向平均状态的变化。也就是说，当指示的变化导致具有kasymp;6-8的准静止自由波的中纬度波导的纬向分离时，通常较弱的波数m=6，7或8的中纬度波动对准静态热源/汇和地形源/汇的响应也许可以通过准线性化强烈放大。

Ⅱ.方法：行星波准共振理论

在我们的研究中，我们在等效正压水平（EBL）的球体上使用线性非稳定，无辐散正压涡度方程。考虑到EBL的假设高度[500-300hPa，（20,24）]，我们将这个等式写成如下的地转近似形式（也参见方程S1a）：

[1]

在方程1中，t是时间；lambda;是经度；phi;是纬度；Omega;和a分别是地球的旋转角速度和地球半径；T是恒定不变的参考温度；Delta;是单位球面上的拉普拉斯算子；alpha;=u/acosphi;是大气环流指数，其中u是EBL的局地纬向平均风；h_or是大尺度的地形高度；alpha;_or=u_or/acosphi;，其中u_or是平均高度为h_or的情况下的局地纬向风（17,24）；psi;rsquo;是EBL的流函数；Trsquo;是中层大气的温度，在一般情况下，它描述了热力学的定常分量和不稳定分量以及大气变量的固有自然变率；而k_h和k_z分别是水平涡动粘滞项和垂直涡动粘滞项；H是大气密度尺度上的高度。虽然大气通常是一个斜压到环境，但在研究中，我们在EBL到条件下在方程1中应用了正压大气涡度。考虑到伴随相应最大值和最小值的地理位置高度的微弱偏移的极端情况下的中纬度大气环流的近似正压可以由2003年欧洲夏季和2010年俄罗斯热力波动不同压力水平（700hPa，500hPa和300hPa）的相应V的分布（图1）以及2011年美国夏季和1997年的欧洲大洪水中的热力波动（图2）来证明。值得注意的是正如我们的论文中所提出的那样，为了使准振谐机制得以发生，必须在对流层内阻止波动，从而防止波动能量逃逸到平流层。区域内波数6-8（25）的波能够满足该条件。

方程1是一个波动方程，我们首先计算任意准静态（即omega;asymp;0，casymp;0）自由平面波的经向波数l的纬向分布，使用给定的k作为Wentzel-Kramers-Brillouin（WKB）解决方案（19,20）来放在固定版本的方程1右侧为0.这产生了（另见方程5）：

方程2将l²描述为u的函数。l²可能在某些纬度改变符号，即所谓的转折点（TPs）（19-22），所以l可能是一个实数，也可能是一个虚数。如果u也在转折点处消失，后者则代表所谓的临界点（CP）（19-22）。如图19所示，所考虑的自由波的能量在CP处经历强烈阻尼。在une;0的TP处，该波将发生强烈的反射（21）。方程2在任何转折点（20）的附近都是无效的，并且静态自由波能量的纬度依赖性由Ariy函数（20）的平方描述，其对于l²＞0是波状的，否则是其是迅速消失的。上述分析表明，在特殊情况下，对于kasymp;6-8的准静态自由波动，存在两个中纬度转折点，后一波动可能成为在纬度范围（波导）内捕获的高振幅自由波，Lambda;_W，t，限制在两个转折点之间。这是因为在这种情况下，对于这种自由波，在波导的横向边界处仅发生接近零的泄露和吸收，条件是在波导内（i）＞0，l²gt;0，在波导外但是在波导附近gt;0,l²lt;0。至于方程2是在WKB近似（20）中导出的，另外还有两个要求（29-31）：（ii）在波导的内部，|psi;|＜1，Lambda;w，意味着在距离Lambda;_psi;/4pi;的情况下被捕获自由波的经向波长Lambda;_psi;的变化与Lambda;_psi;相比较小，（iii）对于所考虑的被捕获的自由波，波导的总宽度Lambda;w，t超过相关Airy函数（29-31）的特征尺度Delta;_A(SI文本，A.4部分)

通常，中纬度解具有纬向波数m=6,7和8到完全成熟的静态等式方程1具有低振幅（参见参考文献20,26和27）。但是，如果满足条件i-iii，则可能存在这些幅度变得更强的情况。如果纬向平均条件以在中纬度波导中捕获具有kasymp;6-8的准静态自由天气波的方式改变，则可能发生这种情况。然后，解决方案 在kcong;m的情况下，对于被捕获的自由天气波，对于m=6-8的完全成熟的静止方程导致对应的振幅，的V，在波导内部（另见式S15）：

条件是（iv）这个经向的自由波数落入范围Delta;，在内给出了对于准静态地形图的组合幅度的主导贡献和方程1右侧的热力条件。（SI文本，A.3节）因此，在方程3中，L和Ro是用于控制方程1中摩擦项中的和的值的涡旋特征Rossby半径和Rossby数（SI文本，A.3节），K=k/a,M=m/a，是的中心纬度。在方程3的作用下，对于波数m，可以在k→m的情况下达到高的准振谐值。我们在下面参考波模式，其中来自准振谐波数m=6，7,8的贡献特别大，分别表示为波6，波7和波8，从而将平面Rossby波共振（32）的概念扩展到依赖于纬度的的情况。

Ⅲ.观测数据的处理

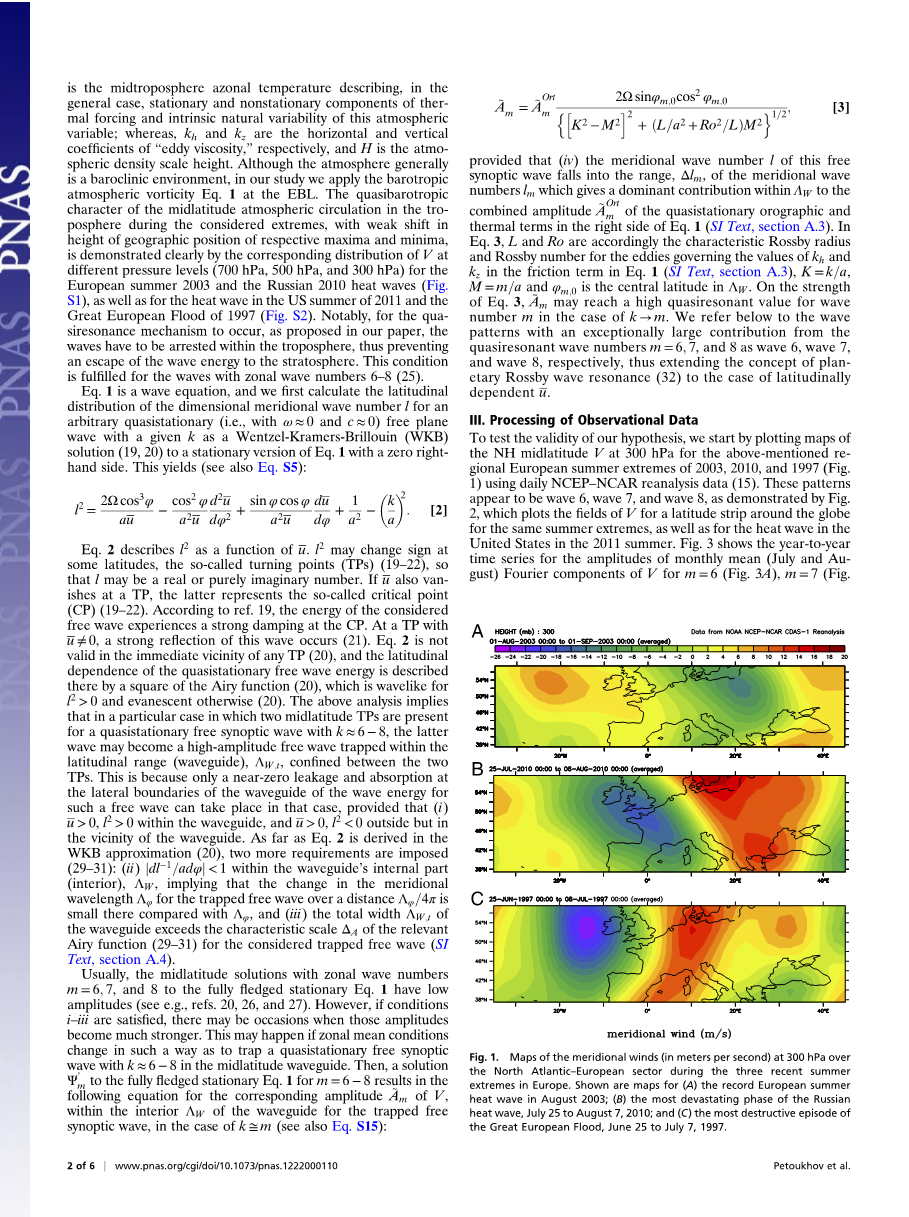
为了验证我们的假设的有效性，我们首先在上述欧洲2003年，2010年和1997年的夏季极端天气（图1）使用每日NCEP-NCAR再分析数据绘制300hPa的北半球中纬度V 的地图（15）。这些模式表示了波6，波7和波8，如图2所示，它绘制了同一夏季极端情况下和美国2011年夏季的热波动的全球范围内纬度地带的V场。图3显示了月平均值（7月和8月）V的傅里叶分量的年度时间序列，其中在300hPa上，m=6（图3A），m=7（图3B），m=8（图3C）是在（37.5-57.5）°N纬度范围内平均（参见参考文献33）。这些时间序列来自相同的每日再分析数据（15），用于观测和再分析数据的最可靠区间（1980-2011）（34）。在俄罗斯热波动和印度西北部洪水的极端月份（2010年7月15日至8月15日的月份，以下简称为2010年7月），美国2011年7月，1983年8月，1984年8月，1994年7月和1997年8月的热力波动，都有m=6的分量非常强（在300hPa时振幅大于4m/s）（图3A）。在2003年8月和2010年7月的极端情况下，m=7的分量的幅度也明显大于通常的值（在300hPa时约为4m/s，图3B）。关于m=7的分量的类似情况还发生在1983年7月，1989年7月，1997年8月，2000年7月，2004年7月下旬/8月初和2009年7月（图3B）。最后，m=8的分量（图3C）在2011年7月，2006年7月，2004年8月和1987年8月具有高振幅（在300hPa下约2.5m/s）。上面列出的所有月份都表现出每月m=6,7,8的傅里叶分量，从相应的m从1980到2011年每月的气候学V可以得到约1.5的标准差（图3A-C）。所有这些月份的特征是在近地表温度、降水和土壤湿度方面具有破纪录的区域极端特征（SI文本，段落A6）。因此，它们可能被称为极端月份，因为它们处于上述区域气候参数的最高值的10％。图3A-C中的斜点虚线分别表示波数m=6,7,8在1980-2011年的时间内的线性回归。如图3A-C所示，波数为6的振幅的相应线性趋势在7月和8月接近于0，而波数7和8在两个月中表现出中等的正线性趋势。

图一 在欧洲最近的三个夏季极端情况下，北大西洋-欧洲地区300hPa的经向风（以m/s为单位）的地图。图为（A）2003年8月记录的欧洲夏季热力波动的地图；（B）2010年7月25日至8月7日俄罗斯热力波动最具破坏性的阶段；（C）1997年6月25日至7月7日欧洲大洪水中最具破坏性的一个

图二 近四个夏季极端情况下，300hPa的全球（经度）中纬度经向风（以m/s为单位）的地图。（A-C）在图1的类似面板中描绘的极端情况的映射。（D）2011年夏季热潮最严重的阶段（7月15日至31日）在美国，可以清楚看到区域波数m=6（B和D），m=7（A），m=8（C）的强贡献的准振谐模式。

图三 1980年至2011年300hPa经向风的傅里叶分量在37.5-57.5°N纬度带上的月平均振幅（以米为单位）。具有7月（绿色）和8月（蓝色）的纬向波数m=6（A），m=7（B）和m=8（C）的波分量显示出了各自的幅度。每个点上的方块都描述了这些月的振幅具有上述波分量的拟线性条件。在每个点上，倾斜的虚线显示了相应的以月为单位的时间序列的线性回归，而水平虚线描绘了相应的1980-2011月度的气候学1.5标准差。

Ⅳ 纬度波导和准振谐波6，波7，波8模式

正如上面所讨论的，波6，波7和波8模式可能与在中纬度波导内捕获具有kasymp;6-8的准静态自由天气Rossby波有关。这在图4中有所表示，对于欧洲2003年热力波动最具破坏性的事件（7月31日至8月14日期间瑞士和法国的最高温）和2002年易北河和多瑙河洪水（8月4日至13日期间该地区的暴雨天气），图中指出了“静止波数”（去除y轴），其中是指300hPa的绝对涡度（19,20）的经向梯度。同样在图4中还表示出了类似的曲线，用于1993年8月1日至15日的非共振谐的情况（准静态纬向波数m=6,7,8的振幅）。基于方程2，和之间的差异仅仅给出了一个给定的k的。图四中右手y轴上k的非线性尺度使得曲线与水平线k=的交点的横坐标给出了带有纬向波数的波的转折点的纬度。在图4中，曲线与水平线k=有两个交点的情况下，这些点的横坐标表示波导的纬度边界（转折点），其中可以捕获自由波k=。根据方程3，如果对于

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[19200]，资料为PDF文档或Word文档，PDF文档可免费转换为Word