迈克尔逊干涉仪和时间脉冲序列的连续性（一致性）外文翻译资料

英语原文共 5 页，剩余内容已隐藏，支付完成后下载完整资料

迈克尔逊干涉仪和时间脉冲序列的连续性（一致性）

Rahul Dutta,* Jari Turunen, and Ari T. Friberg

Institute of Photonics, University of Eastern Finland, P.O. Box 111, Joensuu FI-80101, Finland

*Corresponding author: rahul.dutta@uef.fi

Received October 21, 2014; accepted November 17, 2014;

posted December 1, 2014 (Doc. ID 225385); published January 7, 2015

我们通过一个装有倾斜的反射镜可构建具有与部分时间相干性脉冲序列相关联的两次互相关函数（MCF）的等路径迈克尔逊干涉仪来说明产生的干涉图案的时空分解测量。如果脉冲是似稳态（准静止）的，即相干时间小于脉冲宽度的25％，则迈克尔逊干涉仪的常规时间积分测量提供了正确互相关函数。只要脉冲的平均时间上的强度分布是已知的，且如果时间相干性的复杂度独立于绝对时间，结合适当的校准过程，这种时间积分测量是足够用于互相关函数的确定。

我们知道许多重要的脉冲光场是时间部分相干的。这些包括脉序列的冲生成，在例如准分子激光器、自由电子激光器，和有噪声情况下的锁模激光器中。对于在微结构化的纤维中超连续谱（SC）光的产生也同样如此。借助两次互相关函数，这些脉冲序列的时间相干性可以用非稳定光的二阶相干理论的精确术语来描述。不幸的是，尽管间接技术进来已经提出了超连续脉冲序列，以及在一种测量单个脉冲合奏的复合波形式下互相干函数数值构造是可能的，两次互相干函数的测量不存在简单的方法。

迈克尔逊干涉仪是测量稳定光的时间相干性的标准工具。然而，在脉冲光的情况下，由干涉仪引入的时间延迟代表着两个随时间变化的相干副本的相对时间强度，因此干涉条纹的能见度变得具有时间依赖性。其结果是，时间积分可见性不是时间相干性的真实量度：即使脉冲序列完全相干，在这意义上所有的脉冲完全相同，人们将会观察到可见度降低的条纹。尽管有这一基本问题，标准迈克尔逊实验（或其他基本等价的分裂和延迟安排）有时被用来估计脉冲序列的时间相干性。在这信中我们表明，某种情况下用这种方法可以得到可信的结果，但通常来说，干涉图样的时间分辨测量是必须的。人们提出了适当的设置和对两次互相关函数测量的一个详细配方。我们还表明，在某些条件下，古典迈克尔逊实验的结果可以被校准以提供正确的时间相干性的函数。

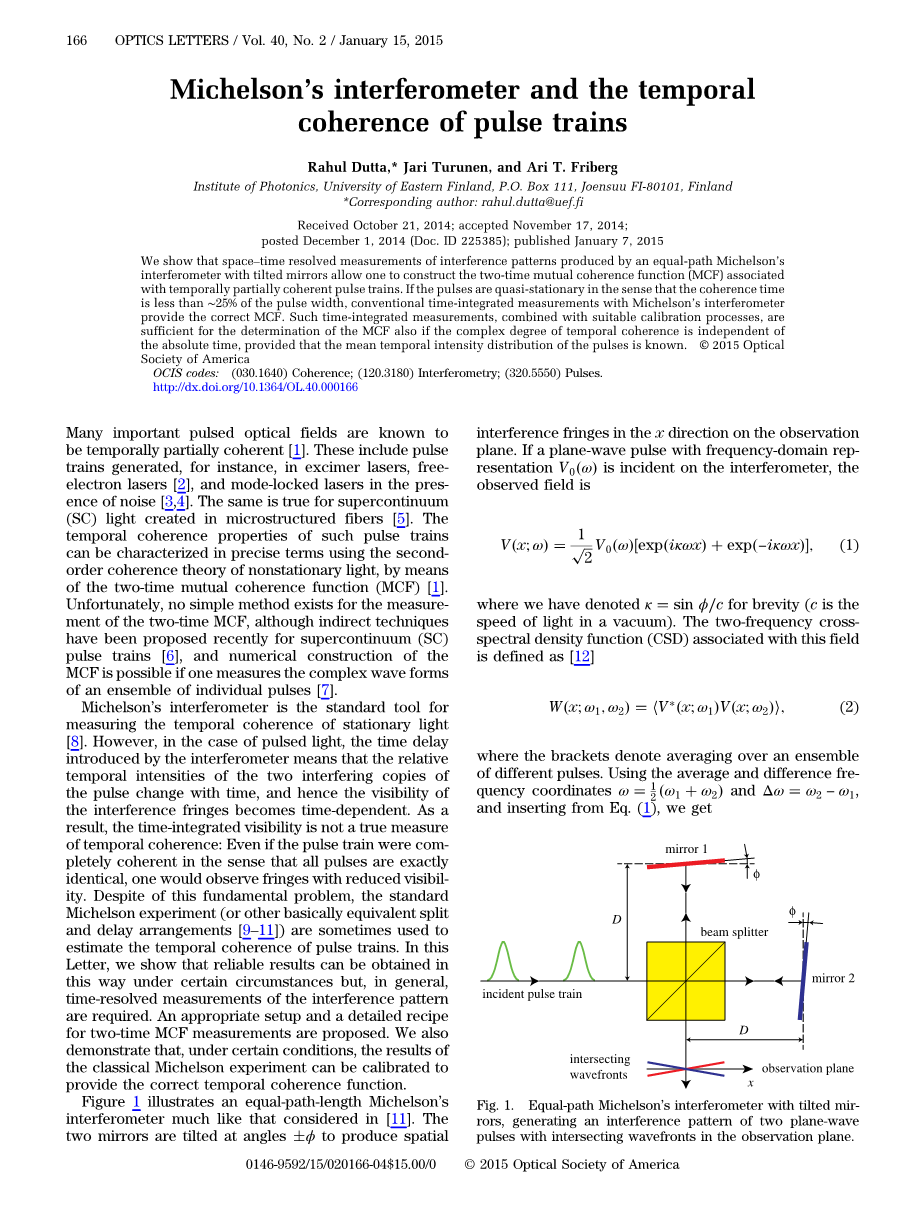
图中示出了一个相等的路径长度迈克尔逊的干涉仪很像在。两个反射镜以角度plusmn;ϕ倾斜，进而产生在观察平面的x方向的空间干涉条纹。如果一个频域表示 平面波的脉冲 是在干涉事件，所观察到的领域是

在这里我们表示简洁（c是真空中的光速）。双频互谱密度函数（CSD）与该领域相关的定义是

括号表示平均的是不同脉冲的集合。用平均差频 得到坐标

图1。等光程迈克尔逊干涉仪的倾斜的镜子，产生两在观察平面相交的平面波脉冲波前干涉图样。

在 是与入射脉冲的CSD。

wiener–khintchine定理的广义非平稳光美国酒店提供的观测时间在两人面：

在 和 是平均化的时间坐标。从式（3）插入，

在HGT与入射脉冲的MCF。空间–时间强度分布因此读

如果我们进一步介绍两时间复杂度的入射场的连贯性， 写

我们发现

在 代表时间相干性的复杂程度相。

条纹的干扰模式中的点x在观察平面的可见性（对应的时间差 ）成

因此， 如果是已知的，| |可以检索从空间的时间能见度测量。乳腺癌的阶段是以条纹的空间–时间位置的确定。因此，两次MCF的构建可以从测量。如果需要，两频率CSD然后可以通过反相式计算（4），提供所有的二阶相干特性的脉冲序列。

虽然很清楚从式（8），时间分辨的干涉图样测量所需的检索两次MCF，不需要测量的干扰脉冲的波形复杂（这是可以做到的，例如，使用成像Xfrog设备[ 13 ]）；的时间强度测量作为一种空间定位功能是足够的。但是，如果一个检测的时间集成的干扰模式 为充分固定的领域，一个自动失去对复杂程度的连贯性不依赖的所有信息，通常不能恢复其Delta;T依赖。这样的时间整合一般会降低的干扰模式的可见性，并导致有效分布的时间相干性，低估的真实值

让我们进一步考虑的一个重要的特殊情况 ，即我们认为的复杂程度的连贯性是一个函数的时间差只有。换句话说，我们假设时间相干性是未在数组中的单个脉冲的时间尺度，特别是对于低精细度谐振器的一个很好的近似，如准分子激光谐振腔。积分方程（8）随着时间的推移，我们有

与知名度由Eq.（9）采取的形式

因为在这些表达式的积分可以计算（在任何位置）当入射场的强度分布是已知的，我们可以校准时间的综合测量检索 正确的分布。此外，由于边缘位置的时间是固定的，我们可以从时间的综合测量确定 。因此，没有时间分辨测量的干涉图案是必要的。

专业 形式更进一步，我们假设一个准稳态脉冲序列

现在的复杂程度的连贯性是一个“窄”的功能相比，时间的强度分布，即，相干时间是短的脉冲持续时间和脉冲的强度分布的假设是平滑的连贯性时间尺度。现在从情商。（8）及（9）

和

因此，虽然干扰模式随时间变化，时间依赖性是相同的在每一个空间点和能见度是独立的时间。因此，标准的迈克尔逊的实验足以确定准同步脉冲的时间相干函数列车直接。

对理论结果进行了验证和评估该方案的实际可行性，我们最后将前面的公式，高斯谢尔模型脉冲平面波。使用符号，两次CSD是

和

在omega;0是中心频率，Omega;是脉冲的带宽，和Sigma;是光谱相干宽度。利用广义维纳-辛钦定理–，我们发现这两个时间

和

在 ，T为脉冲持续时间，和jjrr是相干时间。在光谱和时间域的参数满足

在哪一个域中，在两个域中，有一个方便的度量。我们也有表达

和

用于脉冲列车的时间-带宽乘积。全相干是在极限 wweert获得，和脉冲序列的准静止在极限 。

如果我们引入归一化的时空坐标 ，式（8）所采取的形式

干涉条纹的可见性变得

由于复杂程度的连贯性是独立的，我们可以用公式标定策略（11）检索时间综合测量的真实 fsdgsdd。我们到达一个简单的结果：

因此，如果我们衡量beta;从可视化的空间衰减，我们可以计算出相干alpha;Eq.真度（23）。我们注意到，在相干极限 ,测量能见度会的形式 ，这将导致错误的结论没有校准的脉冲的时间相干性

研究的条件下，脉冲列车是足够准静止的，允许使用标准的迈克尔逊实验的兴趣。图2和图3说明了干涉图案和条纹可见度分布对 宽带脉冲参数的两种选择。在图2中我们考虑的情况下， ，即脉冲宽度和相干时间是同一量级。图2中的“交叉”（一）说明了该地区的脉冲串的交叉副本具有高强度，我们观察到一个强大的时空变化的能见度在大部分地区的脉冲重叠。现在，由于，校准

基于式（26）

在图3中，我们认为一个不连贯的情况下，与0.25。现在的条纹被限制在一个小的横向区域内的脉冲串的重叠区域，和在该区域的干扰脉冲的整个持续时间内的能见度保持几乎恒定。因此，本场可考虑充分运用允许标准迈克尔逊的实验是用。随着Omega;∕omega;0其他值的数值实验也支持这一法则的准稳态区开始在alpha;0.25，即相干时间应小于一季度，脉冲持续时间

在图3中，我们认为一个不连贯的情况下，与0.25。现在的条纹被限制在一个小的横向区域内的脉冲串的重叠区域，和在该区域的干扰脉冲的整个持续时间内的能见度保持几乎恒定。因此，本场可考虑充分运用允许标准迈克尔逊的实验是用。随着Omega;∕omega;0其他值的数值实验也支持这一法则的准稳态区开始在alpha;0.25，即相干时间应小于一季度，脉冲持续时间

鉴于上述结果，我们可以得出结论，标准迈克尔逊的实验是足够的时间相干性的测量，例如，受激准分子激光器和自由电子激光器，如一个被认为在[ 10 ]。然而，它始终是值得检查的校准过程是否引入上述变化的结果。在更多的相干信号源的情况下，如锁模激光器噪声或近相干超连续脉冲，时间分辨测量是最有可能需要。

这项工作得到了芬兰省科学院的部分资助，项目268480。作者也承认院长的特殊支持连贯研究在东芬兰大学，约恩苏（项目930350）。

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[31382]，资料为PDF文档或Word文档，PDF文档可免费转换为Word