
英语原文共 4 页,剩余内容已隐藏,支付完成后下载完整资料
一个新的双熵核心真随机数发生器
Ihsan Ccedil;iccedil;ek , Ali Emre Pusane , Gunhanuml; Dundaruml;
1信息与信息安全研究中心,土耳其Kocaeli,41470,TUBITAK BILGEM ihsan.cicek@tubitak.gov.tr
2土耳其伊斯坦布尔Bogazici大学电气和电子工程系ali.pusane@boun.edu.tr,dundar@boun.edu.tr
摘要
基于1D混沌映射的真随机数生成器由于其有限数量的Lyapunov指数而具有有限的熵生成能力。在这项工作中,我们介绍了一种新颖的双熵核离散时间混沌的真随机数发生器架构,可以通过硬件冗余来增强比特流的随机性。我们开发了用于数值模拟的所提出的TRNG架构的定制数学模型,并且表明由所提出的架构产生的熵比单个熵核对称部分高。我们使用实用信息度量:T熵来计算生成的比特流的熵。 T熵计算显示,所提出的架构能够为广泛的参数值产生高熵。作为概念证明,我们在现场可编程模拟阵列集成电路中实现了提出的架构。获得的随机数成功通过了所有NIST 800.22统计测试,没有任何后期处理。据我们所知,这是文献中双熵核心真随机数发生器的第一个硬件实现。
1 介绍
真随机数发生器(TRNG)被认为是任何加密系统中最重要的组件,因为没有确定性密码函数能够在输出上产生比输入更多的熵[1]。 因此,加密系统的不可预测性和安全性在很大程度上取决于TRNG,将其描述为系统中最关键和最关键的组成部分。 由于熵源的带宽有限,基于采样的电气噪声的TRNG设计方法无法满足当代轻型密码应用的具体要求[2]。 基于多重振荡器采样的TRNGs消耗大量的功率和面积用于快速生成随机位[3,4]。 实现一定程度的随机性所需的取消资源是相当大的,通常从轻量级加密的角度来看是不能接受的。
根据遍历理论,混沌状态下的动态系统可以作为信息源[6]。 混沌系统的指数发散和非周期行为的特征是由下面的正值李亚普诺夫指数驱动,使得它们对初始条件的变化非常敏感。在混沌轨迹的时空演化过程中,主要条件的偏差变化很大。虽然混沌系统的非线性动力学是以确定性术语定义的,但是它们在初始条件下对小扰动的高灵敏度使得它们实际上是不可预测的。由于物理实现中现有的电噪声引起的初始条件的连续漂移使得不可能由于有限的测量精度而精确地确定初始条件,因此提供期望的不可预测性。基于混沌的TRNG使用混沌信号作为熵源。基于连续时间混沌的TRNG实现通常占用大面积,并且由于实现定义动态系统的微分方程所需的大量模拟组件(例如OPAMP,振荡器,OTAs和电感器)而消耗高功率。相反,使用少得多的设计资源可以实现离散时间混沌的TRNG,从而为轻量级密码系统提供了紧凑而有效的构建块[9,10,11]。因此,基于离散时间混沌的TRNG被认为与使用标准CMOS工艺的全数字化实现的密码系统更相容,因为它们不需要任何大面积占用的组件。文献中常规的基于离散时间混沌的TRNGs使用单个内同位图作为熵源[9]。在这种方法中,将混沌信号与随机位产生的阈值进行比较。这种方法的主要缺点是所实施的系统对参数的变化具有敏感依赖性,并且对最大可实现的熵和统计特性具有直接影响。例如,混沌控制参数中的任何变化可能不利地影响可用熵,而位提取阈值的偏差将统计偏差引入到生成的比特流。
在这项工作中,我们提出了一种新颖的双熵核心离散时间混沌基于真实的随机数发生器架构,采用硬件冗余来产生较高的熵随机比特,与传统的混沌控制参数变化相比具有较小的灵敏度 单熵核对应。 据我们所知,这是文献中双熵核心真实数字发生器的第一个硬件实现。 本文的组织结构如下:在第二部分中,我们概述了所提出的数值模拟架构的自定义数学模型,并使用实际的信息度量T熵作为随机度量来评估随机性。 第三节简要介绍了在现场可编程模拟阵列芯片上实现所提出的架构的概念验证电路设计,以及相关的测量和统计测试结果。
- 数学模型拟议培训
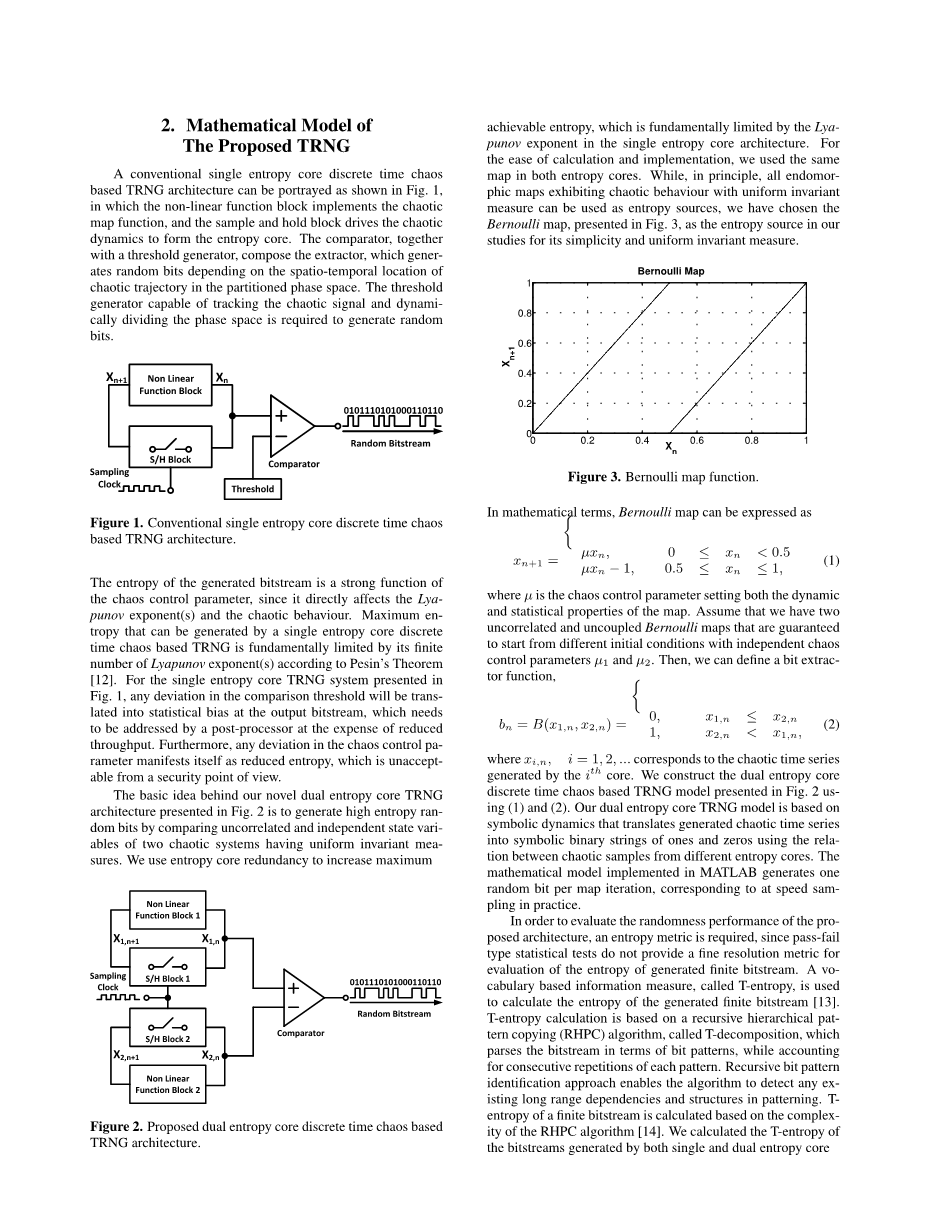
传统的单熵核离散时间混沌TRNG架构可以描绘如图1所示。 1,其中非线性功能块实现了混沌映射函数,采样和保持块驱动混沌动力学形成熵核心。 比较器与阈值生成器一起构成提取器,该抽取器根据分区相空间中的混沌轨迹的时空位置而生成随机位。 能够跟踪混沌信号和动态划分相位空间的阈值发生器需要产生随机比特。
图1 传统的单熵核离散时间混沌TRNG架构。
所产生的比特流的熵是混沌控制参数的一个强函数,因为它直接影响了L·小波夫指数和混沌行为。 可以通过单个熵核离散时间混沌的TRNG产生的最大熵根据派辛定理[12]的有限数量的Lyapunov指数受到限制。 对于图1所示的单熵核心TRNG系统。 如图1所示,比较阈值中的任何偏差将被转换成输出比特流的统计偏差,这需要后处理器以牺牲吞吐量为代价来解决。 此外,混沌控制参数的任何偏差都表现为熵降低,从安全的角度来看,这是不可接受的。
我们的新型双熵核心TRNG架构背后的基本思想如图2所示。通过比较具有均匀不变量测度的两个混沌系统的不相关和独立状态变量来产生高熵随机位。
图2提出的双熵核离散时间混沌TRNG架构。
我们使用熵核心冗余来增加最大可熵熵,其基本上受到单熵核心架构中的Lya-punov指数的限制。 为了便于计算和实现,我们在两个熵核心中使用了相同的映射。 虽然原则上,所有具有统一不变量度的混沌行为的内同位图都可以用作熵源,我们选择了图1所示的伯努利图。 3,作为我们研究中的熵源,其简单性和统一的不变量度量。
|
图3.伯努利地图函数。 |
|||||||||
|
在数学上,伯努利地图可以表示为 |
|||||||||
|
xn 1; |
0:5xn |
1; |
|||||||
|
xn 1 = |
xn; |
0 |
xn |
lt; 0:5 |
(1) |
||||
混沌控制参数在哪里设置地图的动态和统计属性。 假设我们有两个不相关和非耦合的伯努利地图,保证从独立混沌控制参数1和2的不同初始条件开始。然后,我们可以定义一个位提取函数,
其中xi; n; i = 1;2; :::对应于第i个核心产生的混沌时间序列。 我们构建了如图1所示的双熵核离散时间混沌TRNG模型。 2使用(1)和(2)。 我们的双熵核心TRNG模型基于符号动力学,使用来自不同熵核心的混沌样本之间的关系将生成的混沌时间序列转换为符号二进制串的零和零。 在MATLAB中实现的数学模型每个地图迭代生成一个随机位,对应于实际的速度采样。
为了评估提出的架构的随机性能,需要熵度量,因为通过失败类型统计测试不能提供用于评估所生成的有限比特流的熵的精细分辨率度量。 一个称为T-熵的基于vo-calulary的信息测度被用于计算所生成的有限比特流的熵[13]。 T熵计算基于称为T分解的递归分层模式复制(RHPC)算法,其根据比特模式解析比特流,同时考虑每个模式的连续重复。 递归位模式识别方法使得该算法能够检测图案中任何存在的长距离依赖关系和结构。 基于RHPC算法的复杂度计算有限位流的T熵[14]。 我们计算了单熵和双熵核生成的比特流的T熵
- 由单熵核心训练产生的比特流的T熵。(b)由双熵核心训练产生的比特流的T熵。
图4.单熵和双熵核的三维T熵生成比特流比较比较。
TRNG模型,涵盖所有可能的参数值,影响统计属性。计算的T熵的3D投影如图4(a)和(b)所示。注意,在两种情况下,随着混沌控制参数接近理想值2,T熵增加。在单熵核心情况下,Th参数的任何偏差都会大幅度降低0:693的最大可实现熵值,如图4(a)所示。相反,在图1中预先给出的双重熵核心案例中, 如图4(b)所示,最大可实现熵值和相关联的参数间隔都很大,这使得能够在宽范围的参数值下生成高熵比特。我们提出的架构突出,其最大可实现的熵水平超过0:9,适用于各种混沌控制参数,从而超过其高参数敏感对等体。 双重熵核心TRNG架构对混沌控制参数的偏差较不敏感,这从牺牲硬件冗余的实现角度出发,优于单纯熵核对应。 此外,它不需要比较阈值生成器。
3. FPAA的实施和测量结果
现场可编程模拟阵列(FPAA)是一种成本高效的可重构平台,用于模拟电路的快速原型设计。 对于每个熵核心,需要非线性功能块和采样保持块,其可以使用在FPAA芯片的计算模拟块(CAB)中找到的资源来构建。此外,位提取器功能(2)可以通过使用可用CAB内的比较器组件来实现,如图5所示。我们使用基于开关电容器的FPAA芯片(AN231E04)作为提出的架构概念设计的实现平台,因为它允许实现离散时间系统[15]。该芯片由3.3V DC供电,由16MHz主时钟驱动,用于合成CAB组件时钟。 基于双重伯努利图的TRNG的非线性动力学由2MHz工作的采样保持电路驱动。 如图6所示,实现超过1.5Mbps的平均吞吐量。吞吐量受
图5.基于双重伯努利地图的TRNG的FPAA实现。
图6.在FPAA上实施的基于双重伯努利图的TRNG的测量结果。
FPAA的开关电容器实现技术的限制。 现成可用的FPGA开发板用于获取和传输400 Mbits数据到计算机进行统计测试。即使没有一套统计测试可以绝对限定TRNG,它们在确定加密应用程序的统计性能方面是有用的。NIST统计测试套件v2.0用于评估表1所示的采集比特流的统计性能。对应于特定测试的每个p值描述了由理想TRNG生成的比特流的概率[16]。NIST统计测试套件将原始比特流分为1兆位块并应用测试。 表1中的比例列显示通过特定NIST测试的1 Mbit序列的比率。 根据表1的结果,所获得的比特流成功地通过所有NIST统计测试。
表1. NIST STS v2.0测试结果
|
Test |
P-Value |
Proportion |
|
Frequency |
0.904708 |
0.9975 |
|
Block Frequency |
0.783973 |
0.9900 |
|
Cumulative Sums |
0.549331 |
0.9850 |
|
Runs |
0.605916 |
0.9800 |
|
Longest-Run |
0.432672 |
0.9950 |
|
Rank |
0.783973 |
0.9900 |
|
FFT |
0.366918 |
0.9900 |
|
Universal |
0.319084 |
0.9800 |
|
Apen |
0.585209 |
剩余内容已隐藏,支付完成后下载完整资料 资料编号:[28440],资料为PDF文档或Word文档,PDF文档可免费转换为Word |


