带支架加筋板的焊接变形与残余应力的数值和实验研究外文翻译资料

英语原文共 11 页，剩余内容已隐藏，支付完成后下载完整资料

带支架加筋板的焊接变形与残余应力的数值和实验研究

摘要：

这项工作的目的是基于数值模拟和实验，从而能够准确预测焊接引起的残余应力和变形。在具有和不具有三角形支架的加筋板的焊接测试之后，通过非线性热弹性塑性方法数值地研究了焊接变形和残余应力。温度分布和垂直变形的当前数值结果与实验测量结果一致。在本工作中提出的经验公式被证明具有精确预测加筋板中残余应力分布的能力。可以得出结论，支架的存在对分布在加筋板上的残余应力影响较小。然而，具有两个横向支架的加筋板经研究后发现，其最大变形在实验测量中减少74％，在数值模拟中减少67％。

关键词:角焊 实验 有限元分析 残余应力 焊接变形

1简介

加筋板是船舶和海洋结构中的关键结构元素，由于它们的高强度重量比和制造相对简单，广泛应用于各种轻量化结构。在加筋板制造期间，需要大量的熔焊,由此在焊接过程中产生的面外变形和残余应力是一项严重的设计缺陷。由于局部加热，焊接过程中会产生极高的温度。伴随着焊接温度的增加，钢的屈服强度，弹性模量和热导率降低，然而其比热和热膨胀系数增加[1]。焊缝金属与相邻的基体金属在焊接期间加热和随后的冷却循环中产生的膨胀和收缩导致焊接结构产生变形。焊接部件的过度变形导致部件的不对准，并且通常需要昂贵的补救措施如火焰矫直和冷弯将变形降低到可接受的水平[2]。

近年来，人们越来越关注焊接变形的测量，预测和缓解的相关问题。基于1998块板包括普通货船，多用途拖船，散货船，化学品运输船，油轮，研究船以及客货渡轮的试验[3]，船体外壳板多年的焊后变形测量结果发布了。虽然这项工作使用了传统的直接测量方法，近距离摄影测量方法最近已经被更多的使用以获得加筋板和箱形梁焊接变形精确的测量[4，5]，其中板结构的三维（3D）位移场由一系列的数字图像组合而成。

在过去的几年里，数值分析如有限元方法（FEM）已被广泛用于研究结构中焊接引起的变形的分布。双椭球数学模型[6-8]和生死单元法[9]被普遍用来模拟焊接过程中的移动热源。20世纪70年代早期，此时Ueda 等人 [10]开始利用二维模型通过有限元法计算焊接残余应力，随着计算机性能的快速增长，解决传热问题的主要技术正在改变。 Michaleris和Debiccari [11]进行了热弹塑性FEM来预测焊接变形。该方法被证明与实验和经验数据是一致的。 Heinze等人[12]从数值和实验上研究了5毫米厚S355J2 N钢网格密度和连续冷却转变（CCT）行为对焊接变形的影响。Asadi和Goldak [13]提出了一种替代模型，通过从总共48种可能的组合中分析只有14个次级组合，最小化具有6个子通道的管环焊缝的变形。 伪线性等效恒定刚度概念已被用于进行焊接的板的热机械分析，同时散热作为失真缓解的方法[14]。提出的概念被发现在解决类似的热弹塑性非线性问题过程中相比FEM具有更高的计算效率和更简单的计算模型。

研究者不仅研究了焊接变形，还研究了焊接变形残余应力。残余应力是在原材料应力消除后留在固体材料中的应力。焊接过程中产生的热量会引起局部膨胀，它在焊接过程中通过被熔化的金属或焊接部位的布置弥补。当成品焊件冷却时，一些地区比其他地区冷却的更快、收缩的更多，从而产生残余压力。系统的研究表明，不希望出现的残余应力可能会导致对局部应力敏感的故障机制，例如疲劳，脆性断裂，应力腐蚀开裂和蠕变开裂[15]。

Liu 等【16】利用有限元法预测了激光焊接过程中的残余应力场，并用X射线衍射技术对实验结果进行了验证。利用填充焊丝电子束焊接（EBFW）[17]， 对QCr0.8铜合金与304不锈钢的异种金属接头对焊板进行了数值模拟和实验研究。纵向残余应力，通常是对结构的完整性危害最大的应力分量。EBFW的纵向残余应力比自电子束焊（AEBW）低53 MPa。特别是，焊接板中的残余应力的测量需要昂贵的设备和合格的技术员[18,19]。因此，很多研究人员使用简化的数学模型来表示残余应力在板中的分布[20-24]。加筋板残余应力的一个二维参数关系被开发[25]，基于多种板厚和焊接顺序的12个案例研究。

钢托架通常用于防止如船舶和海上平台[26]等结构中支撑部位发生侧向变形或侧向扭转屈曲。这项工作的目的是在数值和实验上研究三角支架的存在对加筋板中焊接引起的变形和残余应力的影响。

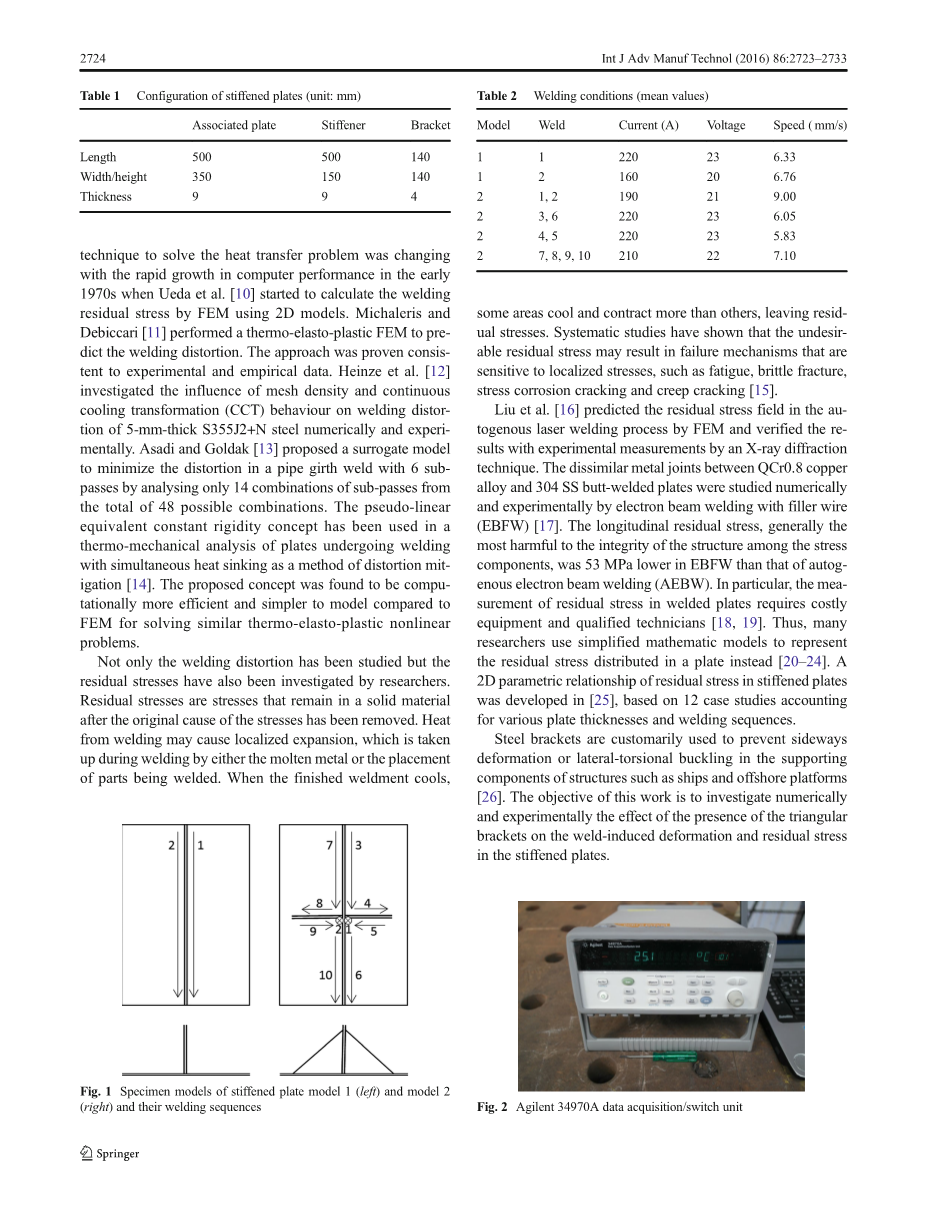
2实验设置 本研究中分析的加筋板是ASTM A36热轧结构钢制造的。表1列出了加筋板的外形尺寸。板和加强肋的厚度为9毫米，支架的厚度为4毫米。无支架的加筋板的情况（简称模型1），首先焊接加劲肋的一侧，另一侧焊接在短时间间隔之后在相同方向上完成，如图1所示。在带有两块加筋板的情况下支架位于加筋板的两侧（简称模型2），首先在垂直方向焊接支架然后开始焊接加强肋。单道熔化极气体保护焊（GMAW）工艺条件列于表2。在焊接试验中，预混80%氩气和20%的二氧化碳作为保护气体。焊丝为林肯S300-RW钢丝，直径1.0 mm。 在焊接过程中，使用K型Agilent 34307A热电偶导线测量板试样的热循环曲线。利用热电偶焊机将热电偶焊接到试板上。 Agilent 34970A数据采集单元（见图2）用于记录测量点的温度数据。焊后变形通过数显千分表测量。

表1 加筋板配置（单位：mm）

表2 焊接条件（平均值）

图1 加筋板模型1（左）和模型2（右） 图2 Agilent 34970A数据采集/开关单元及其相应的焊接顺序

3有限元分析

3.1数值方法

采用单向耦合热弹塑性方法来简化焊接模拟。分别进行热和结构分析，如图3所示。假设结构结果对热变化有影响。所有节点的温度历程首先从热分析计算，然后作为体荷载在同一几何模型中完成机械分析。

图3 瞬态热弹塑性方法流程

3.2热源模型 Rosenthal [27]首先开发了一种温度场的解析解。然而，该解析解在焊缝附近是不适用的，由于其热源几何形状的简化和其忽略的温热物理性能与温度有关的特性。本论文不讨论该解析解。

本论文，使用3D双椭球模型[6]模拟移动热源。该模型预测了温度梯度前部分比后部分更陡，这与实验观察结果一致。热通量沿纵轴的分布为高斯分布;热源的前半部分是一个椭球源的四分之一，后半部分是另一椭球源的四分之一。

对于位于第一/第二半椭圆体内的焊接电弧的前/后部分的一点，体积热通量方程描述为：

其中Q是热源的功率; af，ar，b和c是熔池的特征尺寸; ff和fr是前/后部分的热输入，ff fr = 2.根据焊接条件，热源的参数可以被调节以产生理想的熔化区。例如，Goldak等人[6]得出结论，ff = 0.6和fr = 1.4时，热过程的测量和计算结果具有最佳对应关系。在本论文计算中，参数（af = b = c = 4mm和ar = 16mm）被使用。使用ANSYS参数化设计语言（APDL）代码，热源中心（局部坐标系的原点）在每个小的时间增量内连续变化，从而可以很好的模拟热源的移动。GMAW焊接过程中电弧效率估计为0.7。

3.3温度相关的材料性能

所研究钢板的化学成分和材料性质列于表3和表4中。如表4所示，材料的热和机械性能与温度是高度相关的。例如，钢的屈服应力在室温下为380MPa。但是，在较高的温度420℃下只有原始值的一半，甚至当温度升至1000℃及以上时，屈服应力下降到90％以上。

表3 ASTM A36钢的化学成分（质量％）[32]

表4 ASTM A36钢的材料性能[32]

T温度，C比热，K热导率，alpha;膨胀系数，sigma;y屈服应力，E弹性模量

应注意的是比热和热膨胀系数随着温度的升高而增加，而钢的屈服强度，弹性模量和导热性具有相反的行为。为了实现对经受焊接过程的结构的响应的准确预测，必须考虑温度依赖性材料性质。在非线性应力应变材料模型中，必须考虑加工硬化塑性行为[28-30]。 目前数值计算中，双线性各向同性硬化使用米塞斯屈服准则。

3.4有限元模型

图4显示了焊接试样模型1（无支架）和模型2（有支架）的有限元（FE）模型。单元尺寸的灵敏度分析显示融合区（FZ）和热影响区（HAZ），以及沿厚度方向需要细网格。当试样长度为500mm时，当前分析中最小的单元尺寸为1mm。两者中的角焊缝模型被建模为具有相等边的小三角形。ANSYS 中进行热分析时选择Solid70 3D实体热单元，然后在随后的机械分析中转换为相应的结构单元（Solid185）。SOLID70 3D实体热单元有8个节点且每个节点上只有一个温度自由度。Solid 185实体单元是一个八节点3D单元具有可塑性，超弹性，应力硬化，蠕变，大偏转和大应变能力。

图4 模型1和2的有限元模型

4热结果和验证

4.1模型1

图5显示了无支架加筋板横截面上的六个选定点的位置，用于温度测量。点1和7位于焊接面的中间，点2位于下焊趾，点3-6依次位于距离下焊趾5,10,20和30mm处。由于FZ中的熔池，焊接实验期间仅在5点和6点测量温度。

图5 温度测量的选择点，模型1

用有限元法预测点的温度-时间历程曲线如图6所示。第一道焊过程中，当焊接热源通过时，观察到FZ的中心产生极高的温度（超过1600℃），但随后发生急剧下降。当测量点与焊缝之间的距离增大时，加热的效果会迅速下降。在第6点（距离焊趾28mm），在焊接过程中最高温小于130°C。由于在另一个焊接接头进行了第二道焊，所有曲线在约120s处观察到第二个峰值。在第二道焊进行的7点中，由于热输入比第一道焊低，其最高温度低于第一次焊接（见表2）。

图6 相对于时间的温度曲线，模型1

有限元分析结果与实验数据有很好的一致性（见图7），尽管由于热对流，在曲线的冷却部分存在一些差异，这表明目前的数值方法能够很好的模拟焊接过程。与FZ和HAZ中的温度相反，点5和点6的第二个峰值高于第一个的，原因是第一道焊中HAZ外侧的温度较低。

图7 计算温和测量温度之间的比较，模型1

图8绘制了在参考平面板的顶面上沿横向方向的温度分布。最高温度随时间下降迅速。300s（5min）后，观察到温度基本不变。焊接板在1.5小时后冷却至室温附近。

图8 不同时长的温度分布，模型1

4.2模型2

模型2中所选点的位置如图9所示。点3-6分别距离下焊趾5,10,15和20mm。在焊接方向上，在板的第二半部分的横截面中，点5和6中连接两根热电偶线。图10绘制了带有支架的加筋板横截面中选定点的温度历史预测。由于焊接速度更快，模型2中的最高温度比模型1略低。

图9 温度测量的选择点，模型2

图11显示了数值预测和实验测量两者之间的温度比较，可观察到良好的一致性。应注意，由于支架在横向上的焊接，点5和6的温度之间没有显着差异。

图10 相对于时间的温度曲线，模型2 图11计算温和测量温度之间的比较，模型2

5残余应力讨论

5.1模型1

图12绘制了在加筋板中纵向残余应力的分布。除了起始部分和末端部分之外，在焊缝中观察到显著高的拉伸应力。最大残余应力的大小（360MPa）接近材料的屈服应力（380MPa）。高的压应力（最大133MPa）发生在焊缝附近的区域，而在横向边缘，纵向应力变得非常小。

图12 纵向残余应力分布，模型1

加筋板中部的残余应力分布如图13所示。张力区域的宽度大致等于40mm。。顶层和底层的应力之间存在明显差异，特别是在最大压应力方面。

图13 中段纵向残余应力分布，模型1

5.2理想模型

在国际船舶和海洋结构协会（ISSC）[31]建议的理想模型中，焊接引起的残余应力的分布被理想化为拉伸和压缩矩形块的组合。拉伸应力发生在焊缝中，可假定为材料的屈服应力。压缩残余应力的大小是通过拉伸和压缩部分的平衡要求获得，如下：

其中sigma;Yp是材料的屈服应力，sigma;cp是确定的压应力，b是相关板的宽度，bt表示拉伸区宽度的一半。参数bt对残余应力分布的形状起着重要作用，建议为：

其中tw和tp分别是板和加强件的厚度。

图14绘制了ISSC建议的残余应力分布[31]，并与数值结果进行比较。 但是，它观察到ISSC曲线高估最大值拉伸应力和拉伸区的宽度（71.2mm）。另外，工程曲线忽略了沿着相关板宽度方向压缩残余应力的转。

为了更好地描述残余应力分布，基于[25]中的公式，提出了一个考虑表示真实曲线不同细节的五个参数的新公式。

其中k是比例因子，sigma;y是材料的屈服应力，x是纵向坐标，tau;表示拉伸区域宽度的一半，m是横向变换的因子

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[138435]，资料为PDF文档或Word文档，PDF文档可免费转换为Word