预应力冷挤压模具的分析与设计外文翻译资料

英语原文共 8 页，剩余内容已隐藏，支付完成后下载完整资料

预应力冷挤压模具的分析与设计

摘要:在本研究中对具有预应力圈的冷挤压模具进行了应力分析和设计，也包括计算凹模与预应力圈在接触界面上的接触压力。在这种方法中，弹性有限元方法和拉梅公式分别被用于对模具凹模和预应力圈的分析，并通过运用刚性有限元方法对冷挤压过程进行了模拟。通过使用这种方法和分析已得到的结果，应力分析已经被运用到了过盈配合和冷挤压过程中。通过改变单层或双层预应力圈的组合模具的过盈量和直径比，已经得到了模具的最大有效应力。在结果中，通过将凹模的最大有效应力的最小值来确定过盈量和直径。并且对本文所提出的设计方法和常规设计方法之间所得到的最大有效应力的差异进行了讨论。

关键词：冷挤压 ；接触压力; 直径比; 过盈量; 拉梅方程; 最大有效应力; 组合模具; 叠加原理

1.介绍

用于冷锻的模具设计和分析方法非常重要，因为凹模经受非常高的径向应力和周向应力。对于许多冷锻应用如挤出和锻造，通过用预应力圈收缩来对凹模施加预应力是工业中经常使用的以减少锻模的弹性变形和失效的常用方法。

对于预应力冷锻模的分析和设计，使用拉梅方程分析厚壁空心圆筒的理论通常用于一些假设。然而，很难通过使用拉梅方程来预测凹模的局部最大有效应力，因为大多数模具具有复杂的形状。因此，有关有限元（FE）应用于预应力组合模具的分析和设计的一些研究已经被报道。

通常有两种方法来使用FEM进行组合模具的分析和设计。一个是使用拉梅方程来确定模具的直径和过盈量。在该方法中，由于未考虑挤压过程中的接触条件，在凹模和预应力圈之间的界面上的接触压力具有误差。另一种方法是凹模和预应力圈可以通过使用具有考虑非线性接触问题能力的有限元代码来进行同时分析。在这种方法中，当涉及到许多预应力圈时，为了可以延长分析时间，对于有限元建模来说需要许多的经验。

因此，本文提出了一种快速分析冷挤压模具的方法。包括计算凹模与预应力圈在接触界面上的接触压力。在这种方法中，弹性有限元方法和Lame公式分别被用于对模具凹模和预应力圈的分析，并通过运用刚性有限元方法对冷挤压过程进行了模拟。

通过使用这种方法和分析已得到的结果，应力分析已经被运用到了过盈配合和冷挤压过程中。通过改变单层或双层预应力圈的组合模具的过盈量和直径比，已经得到了模具的最大有效应力。在结果中，通过使用凹模的最大有效应力的最小值来确定过盈量和直径。并且对本文所提出的设计方法和常规设计方法之间所得到的最大有效应力的差异进行了讨论。

2.预应力模的应力分析方法

在本研究中，预应力模具的应力分析过程解释如下所示：

步骤（1）通过使用刚塑性FEM法对工件进行变形分析，进而计算其节点力。

步骤（2）计算工件和凹模之间界面处的工件和凹模的节点力。

步骤（3）计算凹模和预应力圈之间的接触压力，从而得到凹模上的节点力。

步骤（4）通过弹性有限元方法对有负载条件（例如凹模的节点力和接触压力）的凹模进行应力分析。

步骤（5）使用Lame方程计算接触压力在预应力圈上产生的应力。

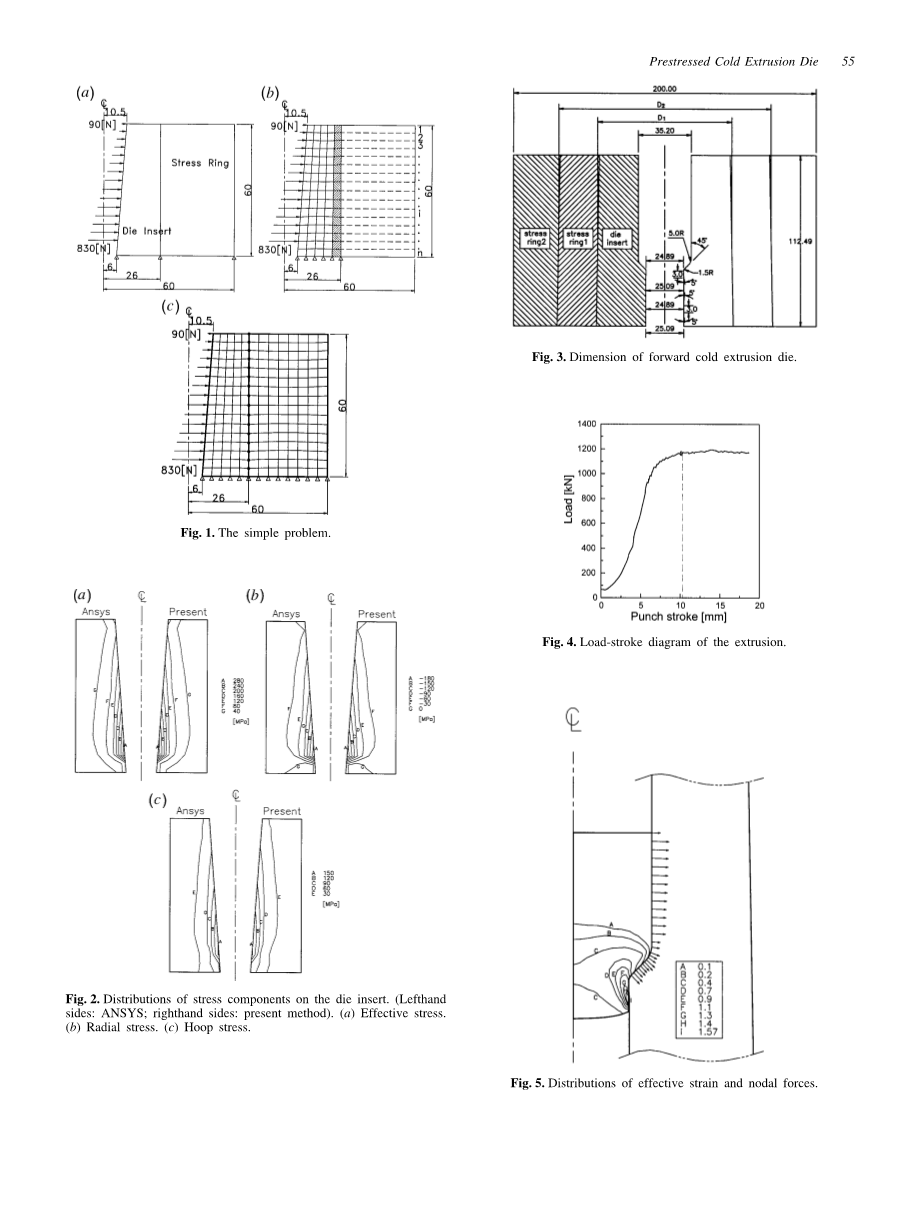
图1 简单问题 图3 冷挤压模具直径

图2 凹模上的应力分布 图4 挤压力加载图

左侧为ANSYS分析法 右侧为本文提出的方法

（a）有效压力（b）径向压力（c）周向压力

该分析过程应用于如图1（a）所示的简单问题。不考虑凹模和预应力圈之间的过盈量。 模具凹模的材料为D2，弹性模量为208GPa，泊松比为0.3。预应力圈的材料为H13，弹性模量为212GPa，泊松比为0.3。 摩擦系数mu;在接触界面处为0.3。图1（b）表示图1（a）中所提出的模型。如图1（a）所示，在凹模的外径处的阴影线元件被称为“外部元件”。 在这个模型中，假设层状预应力圈，如图1（b）所示。层状预应力圈所受的剪切应力被忽略。 图1（c）显示了ANSYS所做的用来分析模具的有限元模型。预应力圈和凹模的接触由接触元件建模

2.1模具凹模和预应力圈之间接触面上的接触压力

通过使用拉梅方程，模具凹模和第一层预应力圈之间的第k层外部元件上的接触条件可以表示为以下形式： (1) 其中，是模具凹模和第一层预应力圈之间的过盈量，是在凹模外部第k层外部元件上的径向位移量，而是在第k层上的第一预应力圈的内侧径向位移量。可以通过使用叠加原理表示。

其中，是由弹性FEM计算出的工作力在第k层外部元件处产生的径向位移。是由于第j个外部元件上的单位正压力产生的在第k层外部元件上的径向位移。 是第j个外部元件上的实际正压力。 是使用拉梅方程（3）计算的，其中，A和B是由预应力圈的尺寸和材料性质确定的常数。

（3）

如果如图（1）所示使用应力环，则B为零，A由公式（4）得出

（4）

其中，Es和Vs分别是预应力圈的杨氏模量和泊松比，r1和r2分别是预应力圈的内半径和外半径。对于两个或三个应力环，常数A和B可以通过拉梅方程来确定。对于锥形应力环，A和B由具有不同半径的每一层分别计算。对于锥角theta;，径向压力由公式（5）计算

=（Costheta; mu;Sintheta;）（5）

其中mu;是凹模和第一预应力圈之间的界面上的摩擦系数。

将等式（1），（3）和（5）和等式（2）表示为线性方程组。（6）

其中Di如下：Di = -A（Costheta; mu;Sintheta;）（7）

图5 有效应变和 图6 凹模的应力分布

节点力分布 左侧为压缩状态，右侧为挤压过程中

(a)有效应力(b)径向应力(c)周向应力(d)平均应力

2.2分析结果比较

图2示出了本文中使用的方法和ANSYS之间的分析结果的比较。 图2（a），2（b）和2（c）分别表示了有效应力，径向应力和周向应力。 可以看出，对于两上述的俩种分析方法，模具凹模上的应力分布几乎相同，因为有效应力，径向应力和周向应力的最大误差分别为0.89％，0.15％和2.63％。 这表明所提出的分析方法适用于预应力模具的应力分析。

3.通过使用刚塑性有限元法分析正挤压过程

对于正挤压的分析，通过使用刚塑性有限元方程开发了一个FE代码。 在分析中使用的工件材料假定为完全退火的AlSi4340合金钢，它的应力 - 应变关系如下

（8）

工件的初始直径为35.2mm，高度为35.2mm。 面积减少50.0％，摩擦剪切因子m为0.1。 模具的尺寸如图3所示。 刚性塑性FE分析的结果可以在图4和5中看到。对于模具凹模的FE分析，从变形分析中获得的节点力必须要映射到模具凹模的网格系统。 在本研究中，Yoon等人提出的方法被用于从工件到模具凹模的节点力的映射。

4.结果和讨论

4.1带有单预应力圈的预应力挤压模具

图3中所示的预应力挤压模具的材料列在表1中。模具凹模和预应力圈的尺寸已通过使用常规设计方法确定。如表2所示，其结果是外径D1为76.2mm，绝对过盈量z为0.249mm。模具凹模的直径比Q = Di / D1为0.462（= 35.2 / 76.2）。其他尺寸在图3中已给出。通过使用所提出的方法，已经分析了预应力挤压模具。其结果示于图6和图7。图6（a）示出了有效应力在模具凹模上的分布。其最大有效应力的值不超过材料的屈服应力WC，如图7所示预应力圈的应力状态不处于屈服状态。图6（b）和6（c） ）分别显示了径向应力和环向应力的分布情况。由于工具材料是脆性的，故而压应力比拉应力好。在WC作为模具凹模的屈服强度的情况下，特别地，应力的状态必须被设计为在压缩状态。平均应力的分布也在图6（d）中示出。然而如图6（d）的分析结果体现出了模具凹模的应力处于略微拉伸的状态。对于厚壁空心圆柱体，拉梅方程用于常规设计，所以这一点没有考虑。

为了确定过盈量，通过用本文所提出的方法对具有变化过盈量的预应力挤压模具进行了分析。分析结果如图8所示。其中，是最大接触压力，是模具凹模上的最大周向应力，是模具凹模上的最大有效应力，和min分别是模具凹模上的最大和最小平均应力。当达到470.16MPa时，预应力圈发生屈服，并在图8中绘制成实线。而常规设计中的结果在图8中用虚线表示。在收缩后，随着过盈量的的增加而增加。

图7预应力圈的压力分布 图8应力、压力和过盈量

（a）压缩后（b）在挤压过程中

然而，如图8（b）所示在挤出过程中，模具凹模上的应力却在减小，径向过盈量由于预应力圈会发生屈服而具有上限，并且由于模具是受压的的，因此具有下限。径向过盈量的设计范围为0.157le;le;0.161。在该范围内，过盈量由的最小值确定，该值为0.161，为1244.0MPa。为了获得进一步优化的设计，通过重复改变新旧俩种方法的外径比，例如采用0.8,0.9,1.0,1.1和1.2等一系列常数，从而决定模具凹模的过盈量，其结果示于图9。在该结果中，发现对应最小值的直径比总是常数0.9的倍数。优化设计总结在表2中。图10展示了通过运用本文所提出的设计方法对具有一个预应力圈的模具的的应力分布。至于设计方面，为1227.37MPa，比常规设计的值低10.07％。

4.2俩个预应力圈的应力分析和设计

如图3所示，在具有两个预应力圈的模具的情况下，模具的材料性质在表3中描述，并且模具的设计参数使用常规设计，如表4所示。锥角为1°，在所有接触面上的摩擦因子为0.3 。

图9、根据多个常数确定的 图10、凹模的应力分布（按本文所提方法）

最大有效应力的最小值（压缩后） 左侧为压缩状态，右侧为在挤压过程中

(a)有效应力(b)径向应力(c)周向应力(d)平均应力

4.2.1变化过盈量的应力分析

图11和图12分别显示了第一和第二过盈量对模具凹模的产生的最大有效应力。 在图11和图12中，区域lt;1gt;和区域lt;2gt; 分别表示第一和第二个预应力圈发生了屈服。 在区域lt;3gt;内进行设计是不可能的，因为第一或第二个预应力圈的过盈量有负值。 从图11（b）和图12（b）中可以看出，径向过盈量由最小值确定。 考虑到加工公差，分别为第一径向过盈量和第二径向过盈量选择0.14和0.05。

为了对常规设计和本文所提出的设计之间的应力状态做出对比，因此进行了应力分析。 结果示于图13和14中。 在图13中，左手和右手图分别是常规和本文提出的设计得到的应力状态。 两种设计都是安全的，因为模具凹模的最大有效应力的值不超过其屈服应力。 结果，在挤出过程中，最大有效应力减小8.2％，最大平均应力增加7.1％至负值。

图11根据过盈量得到的最多有效应力 图12根据过盈量得到的最多有效应力

（a）压缩后（b）在挤压过程中 （a）压缩后（b）在挤压过程中

4.2.2具有两个预应力圈的预应力冷挤压模具的设计

在本节中，已对直径D1和D2进行了挤出模具设计。在表5中，过盈量已由在各种直径条件下的最小值确定。在结果中，当D1和D2分别为67.056mm和117.854mm时，最小为1162.489MPa。从结果中可以看出，总过盈量是在考虑加工公差z1和z2分别为0.22378mm和0.24566mm的情况下选择的。在这些值的条件下，模具凹模上的最大有效应力为1181.253MPa，如图15和图16所示。

表一、单个预应力圈模具的材料性能

表二、传统设计方法和本文所提设计方法的不同设计尺寸

图13应力分布比较 图14预应力圈的应力分布

（a）、（b）为有效应力（c）、（d）为平均应力 （a）传统方法（b）本文方法

图15应力分布比较 图16 预应力圈的应力分布

1. 有效应力（b）平均应力

表3俩层预应力圈模具的材料性能

表4两层预应力圈的模具的设计参数

表5 磨具直径和过盈量的分析

5.结论

在本文中，提出了一种对具有预应力圈的挤压模具进行应力分析的方法。这种方法已被应用于具有一个和两个预应力圈的冷挤压模具的分析。根据具有一个和两个预应力圈的挤出模具的过盈量和直径的变化，评估了其最大有效应力。对于挤出，平均应力，最大接触压力和最大环向应力随着改变收缩配合的过盈量而发生线性变化。在挤出过程中，根据直径和过盈量的变化，模具凹模上的最大有效应力具有最小值，直径和过盈量由本文提出的方法——考虑最大有效应力的最小值和加工误差来决定。因此，可以通过使用所提出的分析和设计方

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[140612]，资料为PDF文档或Word文档，PDF文档可免费转换为Word