
英语原文共 6 页,剩余内容已隐藏,支付完成后下载完整资料
2012 American Control Conference Fairmont Queen Elizabeth, Montreacute;al, Canada June 27-June 29, 2012
一个通用的粒子群优化matlab函数
Soren Ebbesen, Pascal Kiwitz, Lino Guzzella
摘要
粒子群优化(PSO)正在迅速普及,但在MATLAB的PSO算法的官方版本尚未公布。在本文中,我们提出了一个通用的粒子群优化MATLAB函数。界面功能所需的语法与fmincon和ga等现有MATLAB函数实际上相同。我们通过两个例子来展示我们的PSO函数:第一个例子是一个学术测试问题;第二个例子是优化混合动力传动系中传动比的简化问题。且PSO函数在网上可以获得。
1引言
粒子群优化是一种数值搜索算法,用于找出使给定目标或适应度函数最小的参数。PSO算法由Kennedy和Eberhart在二十年前引入[1]。多年来,由于结构简单及其性能良好,PSO得到了显着的普及。适应度函数可以是非线性函数,并且可以受到任何数量的线性和非线性约束。许多出版物,如文献[2]-[6]等等,都展示了PSO在不同应用领域的优点。
MathWorks公司的MATLAB是一种被广泛使用的数值计算软件,虽然MATLAB为数值优化提供了几种算法,但尚不包括PSO算法。2003年,Birge [7]发布了MATLAB的PSO函数。此外,PSO算法的其他一些最新的实现可以从MATLAB文件交换服务器在线获得,例如Evers的PSO Research Toolbox。然而,这些都没有附带公布的文件。
Birge所提出的PSO函数是一个简单但可行的实现。不幸的是,它的语法与标准的MATLAB优化函数(如fmincon和ga)显著不同。因此,不能避免涉及不同搜索方法之间的切换。此外,虽然PSO算法非常适合于并行计算,但该函数不容易在MATLAB分布式计算服务器上实施。
在本文中,我们介绍了一个适用于MATLAB的通用PSO函数。用于连接函数的语法与fmincon和ga的语法几乎相同。此外,还可以规定是否对适应度函数进行向量化。在这种情况下,向量化意味着函数接受输入值的向量,并将返回相应输出值的向量,而不是在此时使用一个输入调用函数。这可以显著地减少运行时间,并使算法能够在计算机集群上运行。其他有用的功能包括指定混合函数的可能性,例如fmincon或fminsearch,其在PSO算法运行终止之后自动继续优化。此外,可以在算法运行时周期性地调用用户定义的输出和绘图函数。而且,我们的PSO函数使用户能够从中间状态恢复群集,而不是重新启动优化,以防由于某些特殊事件函数过早终止。最后,为了简单起见,该函数和所有必要的子函数都包含在单个文件中。
本文的结构如下:第二部分介绍了粒子群优化算法;第三部分介绍了通用PSO MATLAB函数接口所需的语法和命令;第四部分通过两个例子证明了所提出的函数;最后,第五部分为结论。
2粒子群优化
粒子群优化是一种随机搜索方法,灵感来源于群体动物协调运动。每个粒子的方向和速度的变化是认知、社会和随机影响所产生的。所有种群成员的共同目标是找出特定搜索空间内最有利的位置。从数学角度来讲,粒子群优化可以用来求解形如下式的优化问题:
(1)
subject to :
(2)
其中x,b,beq,lb和ub是矢量,A和Aeq是矩阵。函数f(x),c(x)和ceq(x)可以是非线性函数。适应度函数f(x)可以量化x的性能。
A.算法
多年来,已经提出了对原始PSO算法的几种修改。我们采用以下直观的表述:
(3)
(4)
矢量xik和vik是第k代的第i个粒子的当前位置和速度。群体由N个粒子组成,即i = {1,...,N}。此外,Pi是每个个体的最佳位置,G是直到当前代的所有粒子中的全局最佳位置。参数gamma;1,2为在[0,1]范围里变化的随机值,alpha;1,2是加速常数。函数phi;是粒子惯性,其产生一定的粒子动量。图1显示了二维空间中粒子群优化算法的图形解释:新速度vik 1是倾向于将粒子保持在其当前路径上的动量的总和;接着飞向它所经历过的最佳位置P;最后飞向种群的全局最佳位置G。最后,新位置xk 1是当前位置xk和速度vk 1的和。
图1.PSO算法的图形解释
B.稳定性
文献[8]提出了群体稳定性的必要条件和充分条件。条件是:
(5)
(6)
这些条件保证收敛到稳定的平衡。然而,它并不能保证所得到的解是全局最优的。
C.约束
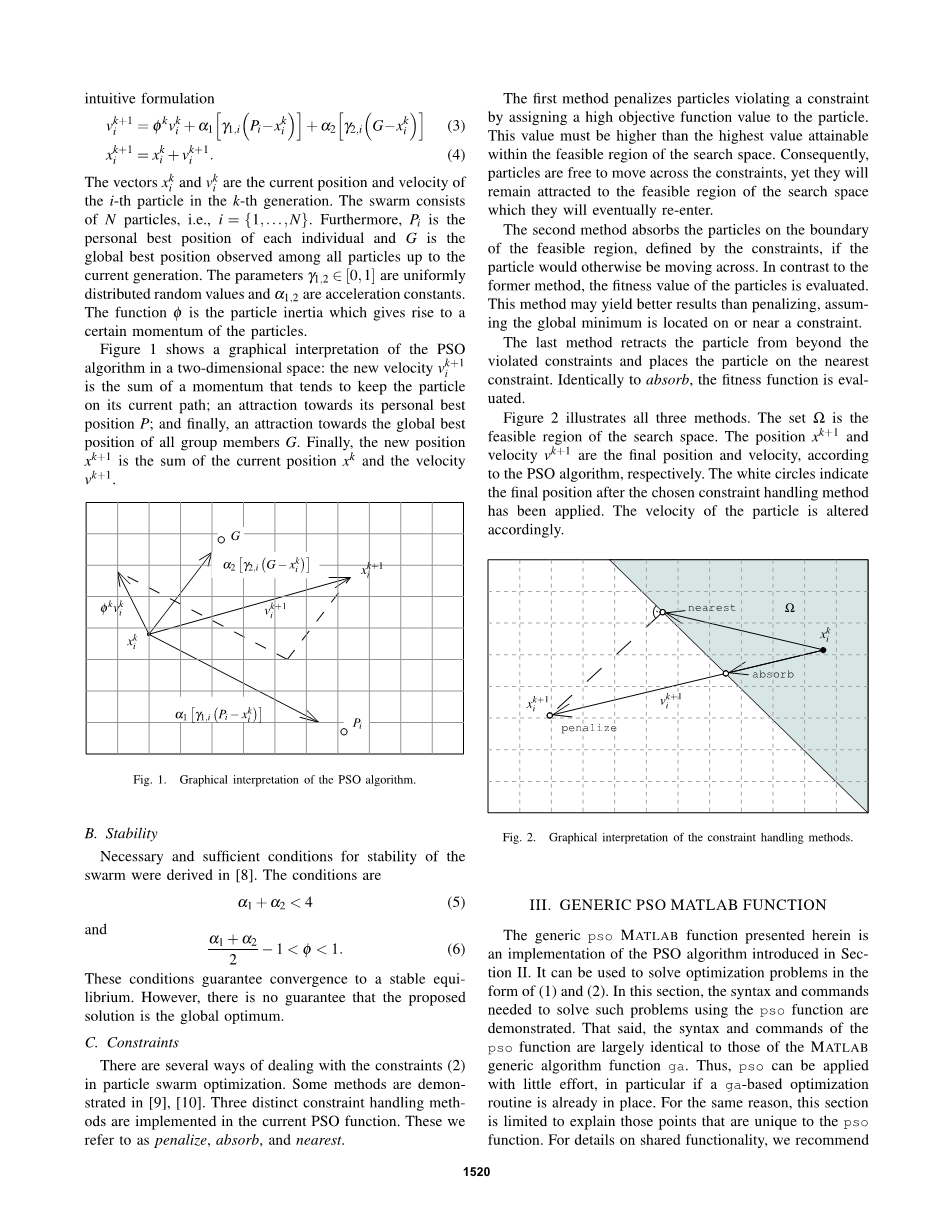
有几种方法可以用来处理粒子群优化中的约束[2]。文献 [9],[10]提出了一些方法。在当前的粒子群优化函数中采用了三种不同的约束处理方法,这些方法被称为惩罚,吸收和邻近。
第一种方法通过为粒子分配高目标函数值来惩罚违反约束的粒子。该值必须高于搜索空间可行区域内可达到的最高值。因此,粒子可以自由地跨越约束,但是它们仍将被吸引到最终将重新进入的搜索空间的可行区域。
如果粒子跨越约束,第二种方法吸收可行区域边界上的粒子。与之前的方法相比,该方法可以评估粒子的适应度值。假设全局最小值位于或接近约束,该方法可能会产生比惩罚更好的结果。
最后一个方法将粒子从违反的约束中退出,并将粒子放置在最接近的约束上。当吸收法一样,该方法可以计算适应度函数。
图2解释了所有的三种方法。集合Omega;是搜索空间的可行区域。根据粒子群优化算法,位置xk 1和速度vk 1分别是粒子的最终位置和速度。白色圆圈表示采用所选择的约束处理方法之后的粒子最终位置。粒子的速度因此而得到了改变。
图2.约束处理方法的图形解释
3通用的PSO MATLAB函数
本节提出的通用PSO MATLAB函数是第二部分介绍的粒子群优化算法的实现。它可以用于求解形如(1)和(2)的优化问题。本节主要展示了使用粒子群优化函数求解这些问题所需的语法和命令。也就是说,粒子群优化函数的语法和命令与MATLAB通用算法函数ga的语法和命令大致相同。因此,应用粒子群优化算法时轻而易举,特别是当基于ga的优化例程已经存在时。基于此原因,本节仅限于解释粒子群优化函数独有的语法和命令。有关共享功能的详细信息,我们建议:可以在http://www.mathworks.com网址获得ga的官方文档
表I输入参数
|
Fitnessfcn: |
适应度函数的函数手柄 |
|
nvars: |
设计变量的数量 |
|
Aineq: |
线性不等式约束矩阵A |
|
bineq: |
b线性不等式约束的向量b |
|
Aeq: |
线性等式约束的矩阵A |
|
beq: |
b向量用于线性等式约束向量b |
|
lb: |
x的下限 |
|
ub: |
x的上限 |
|
nonlcon: |
非线性约束函数的函数句柄 |
|
options: |
通过调用没有输入和单个输出的pso创建的选项结构 |
表Ⅱ输出参数
|
x: |
使适应度函数值最小的变量 |
|
fval: |
x的适应度函数的值 |
|
exitflag: |
整数,标识算法终止的整数 |
|
output: |
包含来自每一代的输出结构体和其他关于算法性能的信息 |
通常使用以下语法来调用粒子群优化函数。
|
gt;gt; [x,fval,exitflag,output] = pso(fitnessfcn,... |
|
nvars,A,b,Aeq,Beq,lb,ub,nonlcon,options) |
熟悉ga或fmincon的用户将会认识此语法。实际上,这些函数和PSO之间语法的唯一区别在于选项结构。为方便起见,每个输入和输出参数的作用分别总结在表一和表二中。或者,可以使用以下语法调用PSO
|
gt;gt; [x, fval, exitflag, output] = pso(problem) |
其中problem是一个包含表I中输入参数的结构体。
A.选项
Options结构体控制了PSO函数的行为。通过调用没有输入和输出参数的函数随时检查PSO可用的选项,也就是说
|
gt;gt; pso |
这将在命令窗口中生成一个输出值,显示所有可用选项、它们的默认值和类别,例如矩阵,标量,函数句柄等。默认选项结构是通过调用没有输入参数并且仅有一个输出参数的PSO产生的。
也就是说
|
gt;gt; options = pso |
表III选项结构(选项)
|
PopInitRange: |
随机初始种群的范围 |
|
PopulationSize: |
群体中的粒子数 |
|
Generations: |
最大代数 |
|
TimeLimit: |
pso终止的最大时间 |
|
FitnessLimit: |
Pso终止的适应度值 |
|
StallGenLimit: |
如果适应度值在StallGenLimit上变化小于TolFun,则迭代终止 |
|
StallTimeLimit: |
如果固定值在StallTimeLimit上变化小于TolFun,则终止 |
|
TolFun: |
适应度值的公差 |
|
TolCon: |
可接受的约束违规 |
|
HybridFcn: |
pso终止后调用的函数 |
|
Display: |
在命令窗口中显示输出 |
|
OutputFcns: |
在每一代后调用的用户自定义的输出函数 |
|
PlotFcns: |
在每一代后调用的用户自定义的绘图函数 |
|
剩余内容已隐藏,支付完成后下载完整资料 资料编号:[138468],资料为PDF文档或Word文档,PDF文档可免费转换为Word |
课题毕业论文、外文翻译、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


