英语原文共 17 页，剩余内容已隐藏，支付完成后下载完整资料

无抗剪钢筋混凝土内部板柱连接冲剪机理试验研究

吴越凡1 ;陈慧2;飞鹏3;和魏建义4

【摘要】：钢筋混凝土平板的冲剪破坏由于其冲剪机理的复杂性和内部破坏机理的直接测量困难,长期以来一直困扰着研究人员。以前冲切试验的测量结果不能为揭示失效机制提供足够的实验证据。在这项研究中，工业内窥镜和特殊设计的应变测量杆安装在柱周围板预留的小孔内，以跟踪具有不同纵向钢筋布置的五个孤立板-柱连接的内部裂缝的发生和扩展。结果表明，临界剪切裂缝是由内部对角裂缝发展而来的，裂缝始于板的中部，并且在柱子周围分布不均匀。内部对角裂缝的扩展与板坯受拉面开始的弯曲裂缝无关，但与板坯受压面混凝土径向应变的卸载密切相关。在冲切失效时刻，临界剪切裂纹从受压区向受拉区扩展，形成冲切失效锥。此外，破坏过程是渐进的，即受压区因临界剪切裂纹不断弱化，导致受压区发生剪切分裂，最终引发连接件的破坏。所获得的实验证据可为板柱连接冲剪机理建模提供物理背景和新思路。 DOI：10.1061/(ASCE)ST.1943-541X.0003222。 copy; 2021 美国土木工程师协会。

作者关键词：平板；冲剪破坏；倾斜的裂缝；失效机制；工业内窥镜

简介 没有抗剪钢筋的钢筋混凝土平板具有冲切破坏的固有风险，这会显着降低结构阻力并导致结构倒塌。因此，研究人员和工程师一直高度关注冲压故障。在过去的几十年中，现有冲切试验的主要目的（ Elstner和Hognestad 1956； Kinnunen和 Nylander 1960；Moe 1961；Hawkins等 1971；Marzouk 和 Hussein 1991； Bažant和 Cao 1987； Einpaul等2015、2016 ; Douml;nmez and Bažant 2017; Teng et al. 2018) 旨在研究不同参数对冲压能力的影响。基于测试结果，经验方程（ Yitzhaki 1966; Tian et al. 2008; Yi and Yang 2014）和理论模型（ Kinnunen and Nylander 1960; Alexander and Simmonds 1992 ）。 穆托尼2008；公园等人。 2011； Broms 2016）被提出来解决平板冲切失效的问题。然而，这些模型尚未就剪切传递和失效机制达成共识。一个重要原因是内部斜裂缝的扩展过程和混凝土复杂的应力状态在试验中难以直接观察和测量，现有的试验结果不能充分反映冲剪破坏过程和揭示破坏机理。随着检测技术的进步，研究人员应用了新的方法来检测板坯内部对角裂纹的扩展。关达里尼等人。 (2009) 将测量棒穿过板坯并测量板坯厚度的变化。结果表明，内部裂纹最初发生在极限载荷的50%～70%，极限宽度约为1.0～1.5 mm。此外，还通过测量板坯两面的挠度间接验证了内部裂纹的发生和扩展。易等人。 （2016）在靠近柱子的两个水平方向上布置了三个带有应变仪的测量杆，它们分别固定在板的受压和受拉面上，并使用高频动态应变收集器记录应变数据。结果表明，在冲裁破坏之前出现倾斜的对角裂纹，破坏时从受压区到受拉区形成破坏锥。 Einpaul等人使用了商业坐标测量臂。 (2018) 获得内部裂纹的位置、扩展过程和开口方向。冲切破坏裂纹分为临界剪切裂纹和劈裂破坏裂纹，分别代表破坏前预先形成的内部斜向裂纹和破坏时刻新形成的倾斜度较小的裂纹。在板坯的测试中观察到一种或两种类型的裂缝。仅具有劈裂破坏裂纹的试件，在劈裂裂纹形成之前没有内部裂纹，导致瞬间冲切失效。然而，更有可能的是在测试中没有检测到内部裂纹。在以前的实验研究中已经检测到板柱连接中内部裂纹的发生和扩展。然而，基于现有的试验结果，仍不能完全描述冲切破坏的过程和机理。由于平板冲切失效的复杂性，需要进行室内试验研究其力学行为，这有助于合理地模拟冲切机理。因此，本研究针对无抗剪加固的五个内部板柱连接设计了一个综合观察和测量方案： 1. 使用工业内窥镜直观地检测板内部裂缝的扩展。 2. 动态应变测量杆在柱周围8个径向布置，监测板坯厚度的变化，从而间接检测到内部裂纹的扩展。 3.系统测量了板受压面的混凝土压缩应变。根据所获得的试验结果，对冲剪破坏的机理进行了探讨，为改进理论模型提供了新的实验依据。

实验程序

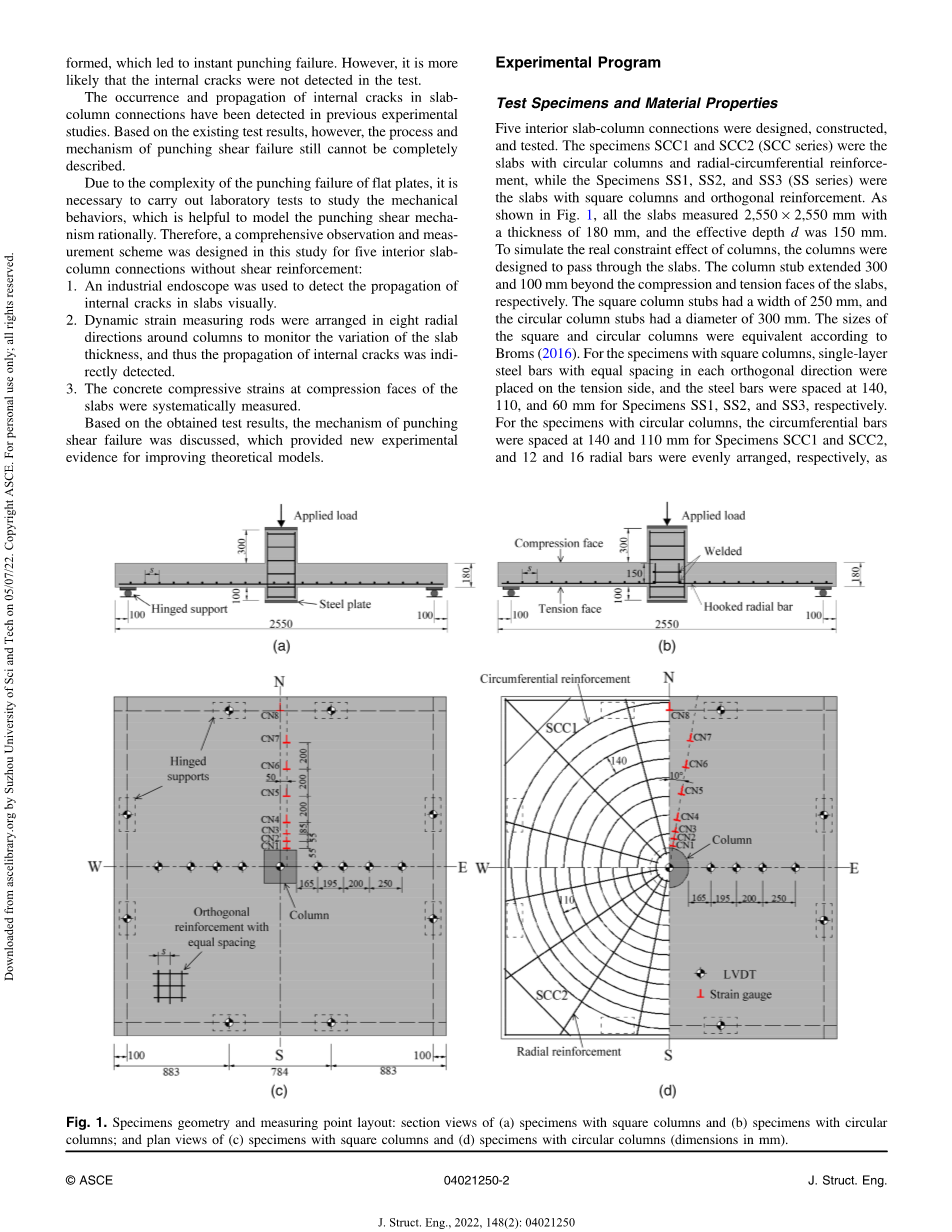
测试样品和材料特性 设计、建造和测试了五个内部板柱连接。试件 SCC1 和 SCC2（SCC 系列）为圆柱板和径向-圆周配筋，而试件 SS1、SS2 和 SS3（SS 系列）为方形柱和正交配筋板。如图 1 所示，所有板坯尺寸为 2550 times; 2550 毫米，厚度为 180 毫米，有效深度 d 为 150 毫米。为了模拟柱子的真实约束效果，柱子被设计成穿过楼板。柱短柱分别超出板的受压面和受拉面 300 毫米和 100 毫米。方柱短柱的宽度为 250 毫米，圆柱短柱的直径为 300 毫米。根据Broms (2016)，方形和圆形柱的尺寸是相同的。对于方柱试件，在受拉侧放置各正交方向等间距的单层钢筋，试件SS1、SS2、SS3的钢筋间距分别为140、110、60mm .对于圆柱试样，试样 SCC1 和 SCC2 的圆周钢筋间距分别为 140 和 110 mm，径向钢筋分别均匀排列 12 和 16 根，如图 1（d）所示。为了防止锚固失效，径向钢筋与最小的环向钢筋焊接，并以90度的钩子弯曲成柱，锚固长度为150毫米[图。 1(b)]。纵向钢筋直径为14 mm，弹性模量为2.01times;105 MPa，伸长率为29.2%，屈服强度和极限强度分别为498和645 MPa。在柱子中提供了足够的加固以防止其失效。表1列出了测试当天试件的圆柱混凝土抗压强度fc 0 。

仪器仪表

在液压千斤顶顶部放置一个称重传感器来测量施加的载荷，在板坯受压面上放置九个线性可变差动变压器（LVDT）来测量板坯的垂直挠度，在千斤顶上放置八个 LVDT。铰支座中心同一面测量支座沉降，如图 1 所示。此外，图 1 还显示了 T 形应变片的位置，用于测量板受压时的混凝土应变面孔。铸件时每块板预留28个孔，位置如图2所示。8个直径为10 mm的观察孔通过工业内窥镜（最小焦距）观察内部裂纹的扩展情况。 0.45 兆像素相机的镜头为 4 毫米，视场角为 120°）。另外20个直径为8 mm的测孔用于安装应变测杆，以测量板坯厚度的变化。应变测量杆由一根铝合金杆和一个附在杆中间的应变计组成（图 3）。其直径为 6 mm，精度为 0.01 mm=10 mu;ε ，测试中以 2,400 Hz 的频率采集数据。应变计也连接到板中的弯曲杆上。

测试设置和测试程序 I

1所示。在底部柱螺柱上粘合了一块20毫米厚的钢板以增强约束。为避免轴承失效和过早压碎，使用 20 mm 厚的加载钢板来传递施加的载荷，并在每个支撑上放置 250 times; 120 times; 20 mm 的支撑钢板以传递反作用力。垂直载荷由布置在柱顶的液压千斤顶施加。测试设置如图 4 所示。使用 1,000 kN液压试验机在负载控制下以 35 kN =min 的速率进行测试，直到出现故障。载荷增量为估计极限载荷的 10%，在接近失效时减少到估计极限载荷的 5%。估计的冲压破坏载荷Vp是根据经验冲压方程 ( Vp frac14; 0.236beta; deth;f 0 crho;fyTHORN;1=3umd 获得的，其中 beta;d 是尺寸效应系数， fy是钢筋的屈服强度，um 是临界截面的周长) 由 Yi 和 Yang (2014) 提出。在每个载荷间隔，保持载荷 10 min 后记录裂纹，直至裂纹稳定。

实验结果与讨论

本节介绍并讨论了试验中获得的实验结果，为后续的冲压机理分析奠定了基础。裂缝模式、破坏模式、荷载-挠度曲线和极限强度描述了五个内部板柱连接在集中荷载下的整体力学行为；受弯钢筋和混凝土的应变间接反映了裂缝引起的荷载传递路径和内应力的重新分布；内窥镜内部裂纹观察和测杆应变测量分别直接和间接捕捉内部裂纹的发生和扩展。

裂纹模式和失效模式

一般来说，试件的破坏过程大致可描述为：当外加载荷（不包括试件自重）为极限载荷的16%～27%时，出现周向裂纹和少量在柱附近的板坯受拉面上产生的径向裂缝。随着外加载荷的增加，径向和周向裂纹逐渐向外扩展。当荷载约为极限荷载的60%～70%时，径向裂纹扩展至板坯边缘。对于方形和圆形柱的试样，周向裂缝分别延伸到距柱边缘约 370 和 290 mm 处。随着荷载的进一步增加，圆柱试件的周向裂缝分布范围停止扩大，而方柱试件的周向裂缝分布范围在荷载约为83%时扩大到距柱边缘约470 mm。的极限载荷。此后，板坯受拉面裂缝的数量和分布保持稳定，但柱附近的裂缝宽度随着外加荷载的增加而显着增加。另一方面，周向裂缝显示出相似的宽度，表明临界剪切裂缝在破坏前没有延伸到受拉面。当荷载增加到极限荷载时，所有试件均发生脆性冲剪破坏，对于配筋率较低的试件，冲切面不规则，距柱边缘260～530 mm范围内出现混凝土剥落[图. 5（a，c和d）]。随着配筋率的增加，板坯受拉面的冲孔锥形状变得规则（[图5（b）中的试件SCC2]，甚至在最大配筋率SS3的试件中没有形成[图） . . 5(e)]. 测试后，沿 N-S 轴锯切所有试样，以检查板坯中的最终内部裂纹图案，如图 6 所示。正如预期的那样，所有试样均在冲切模式下失效. 除试件 SS3 外的所有试件，板坯的冲孔裂缝贯穿整个板截面；而配筋率最大的试件 SS3 的冲孔裂缝在配筋层停止对角扩展并水平扩展。 （图 6）冲孔破坏裂纹随配筋率的增加而减少，预留孔的存在对开裂破坏模式和破坏模式的影响可以忽略不计。

载荷-挠度曲线

图 7 显示了在柱子上测量的试样的载荷-挠度曲线。开裂前，载荷-挠度曲线近似线性，挠度很小。开裂后，试样的刚度逐渐降低，直至达到完全开裂状态。完全开裂后，除试件 SS1 外，所有试件的载荷挠度曲线均变为线性，直至冲压失效，表明试件的开裂后刚度几乎保持不变。如图 7 所示，开裂后刚度高度依赖于配筋率，增加配筋率会增加试件的开裂后刚度。由于钢筋的连续屈服，试样 SS1 的刚度在屈服后显着降低。 Einpaul等人先前的研究。 （2018）提出弯曲响应的第二个转折点（即荷载-挠度曲线）出现在径向钢筋的屈服范围达到rc d（其中rc是圆柱的半径）时。对于本研究的试件，只有试件SS1满足条件（ rc可以用方柱的边长代替），其刚度随着钢筋屈服范围的增大而减小。

极限强度

试样的破坏载荷 Vu 如表 1 所示。正如观察到的，破坏载荷随着抗弯钢筋比的增加而增加。对于 SS 系列，将配筋率提高 27% 和 134%，破坏载荷分别增加 3% 和 21%。可以证实，随着配筋率的增加，极限冲压强度增加而变形减小，这与Kinnunen和 Nylander（1960）的试验结果一致。表 1 显示了测量的破坏载荷 Vu 和预测的弯曲破坏载荷 Vflex 之间的比较， Vflex是通过屈服线理论计算的。图 8 显示了圆柱 ( Muttoni 2008) 和方柱 ( Gudalini et al. 2009) 试件的弯曲破坏载荷的屈服线模式和预测方程。如表 1 所示，Vu= Vflex比随着配筋率的增加而降低。在 SS 系列中，试件 SS1 的最大 Vu= Vflex比为 0.92，这可能表明发生了弯曲故障，但它在冲压故障中失败了。与 SS 系列相比，SCC 系列显示出低得多的 Vu= Vflex比，平均为 0.54，证实了试样所经历的冲压失效模式。同样，由Kinnunen和 Nylander (1960)测试的带有圆柱和径向圆周钢筋的八块板也显示出低 Vu= Vflex比率（0.37 到 0.58）。这可能是因为径向-周向配筋布置加剧了柱附近混凝土的损伤积累，这可以通过楼板的变形集中来体现。图 9 显示了试样在三个选定载荷水平下的挠度分布。挠度是垂直方向的弯曲变形和剪切变形的总和。挠度分布曲线不成比例的局部增加表明板坯变形集中，反映了裂缝扩展或混凝土损伤累积（ Kinnunen和 Nylander 1960； Hallgren 1996； Gudalini等人，2009）。在 SS 系列中，试样的挠度在大约 0.9Vu 之前呈线性分布，而对于 SCC 系列试样，挠度的不成比例增加发生在低得多的 0.5Vu 载荷下。另一方面，当外加载荷超过0.6Vu时，SCC系列板坯受拉面的周向裂纹分布保持不变，而SS系列的周向裂纹逐渐发展到0.85Vu，最终分布范围为远大于 SCC 系列。因此，与SS系列试件相比，SCC系列试件的混凝土损伤积累较早且范围较小，可能导致其冲孔能力较低。

抗弯钢筋应变

图 10 显示了钢筋应变在两个正交方向上不同荷载水平下沿选定钢筋的分布，表明钢筋应变在两个正交方向上向支撑板边缘衰减。如图所示，屈服半径（即钢筋屈服范围的半径）随着抗弯配筋率的增加而显着减小。对于具有最大配筋率的试件，试件 SS3，没有观察到配筋的屈服。样品 SS2 中的钢筋屈服于距中心 500 毫米的范围。应该提到的是，在试样 SS1 中，在冲压失效之前没有形成完整的屈服线机制，尽管试样的最大屈服半径大于中心 800 毫米。对于试件 SCC1 和 SCC2，当外加载荷超过极限载荷的 90% 时，周向钢筋的屈服半径达到 430 到 600 mm，而径向钢筋没有屈服。在径向上，由于径向配筋率随半径的增加而减小，部分外测点的配筋应变接近甚至超过内测点的配筋应变。圆柱试样的冲切强度相对较低，导致钢筋的屈服范围相对较小。

混凝土应变

试件的径向混凝土应变如图 11 所示。可以看出，靠近板边缘的径向应变（量规 CN7r 到 CN8r）可以忽略不计，而柱附近的径向应变在开裂后迅速增加，表明减小压缩区高度。随着载荷的增加，径向压缩应变先增大后减小，这在SS系列中更为明显。压应变卸载半径范围为距柱边缘 30 至 620 mm（量规 CN1r 至 CN6r）。应变片CN5r和CN6r记录的应变轻微卸载，CN2r到CN4r的应变增长率在明显卸载前逐渐减小，而CN1r的应变卸载相对突然。另一方面，CN1r 卸载前的应变曲线形状与载荷挠度曲线相

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[590364]，资料为PDF文档或Word文档，PDF文档可免费转换为Word