利用无网络数据社会行为快照进行网络结构推断及其网络结构影响的研究外文翻译资料

英语原文共 12 页，剩余内容已隐藏，支付完成后下载完整资料

利用无网络数据社会行为快照进行网络结构推断及其网络结构影响的研究

Antonia Godoy-Lorite1,2 and Nick S. Jones1*

像投票和接种疫苗，人们的行为取决于社会网络结构，社会网络结构因行为类型而异，并且这些行为类型通常都是隐藏的。但是我们总是有行为数据，尽管只有一个时间点的快照拍摄。我们提出一种方法，仅仅使用快照人口水平行为数据来共同推断网络结构和人类行为的模型。这个模型利用了几何社会人口统计网络模型和基于自旋的行为模型等几个参数模型的简单性。针对欧盟公投和两次伦敦市长选举，我们说明了该模型如何提供对人口同性恋倾向的预测和解释。我们除了从行为数据集中提取特定于行为的网络结构外，还建立了一个将不平等和社会偏好与行为结果联系起来的框架。潜在的网络敏感政策：在最近的选举中，如何减少两极分化，收入不平等，社会温度和同性恋偏好的变化。

从领导人投票到对疫苗的态度，人类的行为都有可能取决于社交网络的结构。虽然现在已经存在庞大且高质量的社会科学数据集将个人行为和个人属性连接起来，但是想要直接了解某种行为背后的社交网络却相当困难。主要的原因包括：依赖科技的网络数据难以真实地反映社会行为、现有的数据集仅在有限时间和空间内可用、大规模社交网络数据的安全隐私问题。在这里，我们不寻求高精度地推断单个链接，而是寻求特定于行为的网络模型，该模型为社交网络结构提供信息并且与策略相关。了解社交网络结构及其如何塑造行为的需求似乎很迫切：人们担心社交网络在健康中的作用，从拒绝接种疫苗到肥胖，以及反复出现的概念，社会正在变得过度两极分化。通过访问社会结构及其支持的行为动态，我们还可以改善我们的扰动理解：澄清社会不平等的变化如何改变健康和社会两极分化。

鉴于需要表征社交网络结构，因此，从Twitter到手机等大型网络平台的数据引起了巨大的科学兴趣。然而，人们普遍认为，技术平台数据存在许多实际问题。一个主要问题是，依赖于技术的网络数据集是否能真正表明与社会相关的行为（如吸烟或投票）所依赖的社会结构;相反不同的行为很可能分布在我们社交网络的不同方面。依赖于技术的网络数据集具有商业敏感性，因此难以访问和共享，并且通常在有限的时间跨度或空间范围内可用，并且特定平台本身不太可能无限期存在：这引起了对可重复性和可推广性的担忧。然而，最重要的问题，必须限制未来所有这些努力，是大规模社交网络数据的巨大隐私影响：社交网络数据很难匿名化。使用技术平台数据的另一种途径是使用常规调查。除了可扩展性问题之外，从调查中确定推断的网络结构是否与表达特定行为的真实网络相关通常是一个挑战。第三条既定路线是尝试通过时间序列数据等推断网络模型。这些方法通常假设对个人层面的数据进行反复观察;不幸的是，人类行为，如投票或吸烟，通常在单个时间点进行采样。虽然因此访问特定于行为的社会结构似乎具有挑战性，但社会数据有一个显着的特征可以帮助推断：与许多网络系统不同。

人口普查提供各个节点的社会相关坐标信息。彼得·布劳（Peter Blau）提出了一种直观而强大的社会结构理论，使得社会中的每个人都可以被视为高维空间（具有年龄，性别和收入等维度）中的一个点，其中个体之间的联系率由相同属性（同质性）驱动，并取决于他们在空间中的相对分离。这种同质性表明，我们可以考虑个体形成以他们在社会空间中分离为条件的联系。通常，这些网络由软随机几何图（SRGG）建模，其中两个个体之间链接的概率随着它们之间的距离（23）而衰减[与随机几何图（RGG）相反，其中连接是确定性的：如果两个节点之间的距离是在给定的阈值内。除了有关个人坐标的信息外，健康和投票数据集还为我们提供了有关个人行为的快照信息。有完善的理论来表达离散选择（24），这反过来又与有限温度线性阈值影响模型（25，26）和Ising模型（27-29）有关。本文利用布劳的社会结构几何视图和Ising行为模型之间的合并来推断SRGG社会结构模型的内核;我们将其命名为内核-布劳-伊辛（KBI）模型。

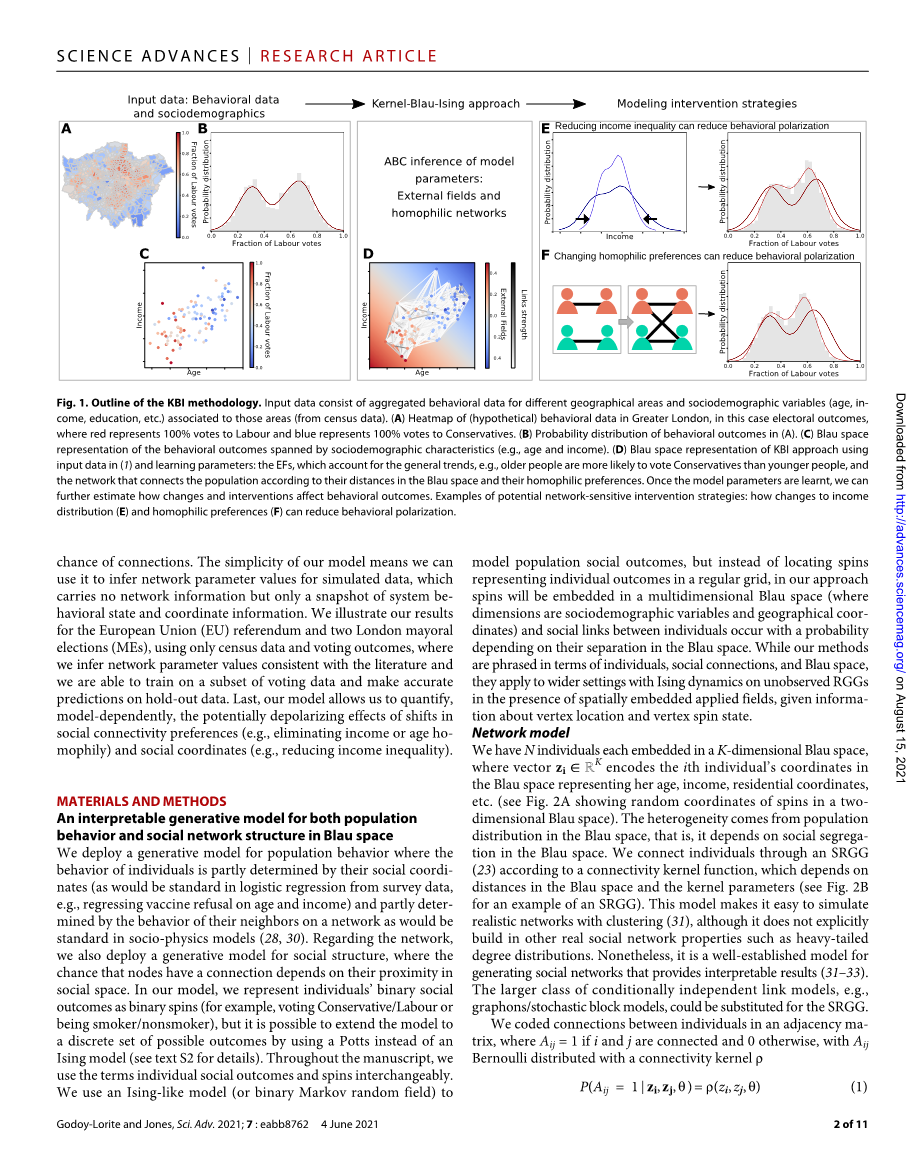
我们的模型使行为取决于社会环境和网络中邻居的行为成为可能。我们在图 1 中说明了这种概念化。它将社交空间中的一组个体作为输入，并调用Ising行为模型和简单（SRGG）模型，了解社交空间中的距离如何影响连接的机会。我们模型的简单性意味着我们可以使用它来推断模拟数据的网络参数值，这些数据不携带网络信息，而只携带系统行为状态和坐标信息的快照。我们仅使用人口普查数据和投票结果来说明欧盟（EU）公投和两次伦敦市长选举（MEs）的结果，其中我们推断出与文献一致的网络参数值，并且我们能够对投票数据的子集进行训练并对保留数据做出准确的预测。最后，我们的模型允许我们量化，依赖于模型，社会连接偏好（例如，消除收入或年龄同质）和社会坐标（例如，减少收入不平等）变化的潜在去极化效应。

材料和方法

布劳空间中人口行为和社交网络结构的可解释生成模型

我们部署了一个群体行为的生成模型，其中个体的行为部分取决于他们的社会协调（这在调查数据的逻辑回归中是标准的，例如，根据年龄和收入对疫苗拒绝进行回归），部分取决于他们的邻居在网络上的行为，这在中国是标准的社会物理模型（28,30）。针对网络我们还为社会结构部署了一个生成模型，其中节点有连接的可能性取决于它们在社会空间中的接近程度。在我们的模型中，我们将个人的二元社会结果表示为二元旋转（例如，投票保守派/工党或吸烟/不吸烟），另外可以通过使用Potts而不是Ising模型将模型扩展到一组离散的可能结果（详情见文本S2）。在整个手稿中，我们交替使用术语“个人社会结果”和“旋转”。我们使用类似伊辛的模型（或二元马尔可夫随机场）来模拟人口社会结果，但不是在规则网格中定位代表个人结果的旋转，在我们的方法中，自旋将嵌入多维Blau空间（其中维度是社会人口变量和地理坐标），个体之间的社会联系发生的概率取决于他们在Blau空间中的分离。虽然我们的方法是根据个人、社会关系和Blau空间来表述的，考虑到有关顶点位置和顶点自旋状态的信息，它们适用于更广泛的设置，在存在空间嵌入应用场的情况下，未观测RGG上的伊辛动力学。

网络模型

我们有N个个体，每个个体嵌入到K维Blau空间中，其中向量在Blau空间中对第i个人的坐标进行编码，表示她的年龄、收入、居住坐标等（见图2A显示了二维Blau空间中自旋的随机坐标）。这种异质性来自Blau空间中的人口分布，也就是说，它取决于Blau空间中的社会隔离。我们根据连接性核函数通过SRGG（23）连接个体，这取决于Blau空间中的距离和核参数（参见图2B了解SRGG的示例）。该模型使得使用聚类（31）模拟现实网络变得容易，尽管它没有明确地构建其他真实社会网络属性，例如重尾度分布。尽管如此，它还是一个成熟的社交网络生成模型，可以提供可解释的结果（31-33）。更大类别的条件独立链路模型，例如graphons/随机块模型，可以替代SRGG。

我们在一个邻接矩阵中对个体之间的连接进行编码，如果i和j是连接的，则，否则为0，并且Aij-Bernoulli分布在一个连接核中

我们选择连接性核为逻辑S形函数，因为它们已成功用于ego网络（15）和潜在空间推理（31–33）上连接性核的推理

其中dij被解释为Blau空间中的距离，0是一个偏差项，它说明了无论Blau空间中的距离如何，总体连接密度，以及k是Blau维度k的连通系数，它加权了k维度中的距离对总距离的贡献。连通系数测量Blau空间中的同质性，以便变得越强，同向性在该维度中越强（连接在该维度中变得更局部化）。恒定偏差项允许重新调整系统大小，因为它可以在不修改连接性内核参数值的情况下考虑密度变化（请参阅文本S3）。连接性核为Blau空间（15）上的连接导出一个可解释的半度量，并可用于生成SRGG的特定实现。

行为模型

我们的伊辛模型将产生如下自旋构型。嵌入Blau空间（坐标为）的每个独立个体i都被旋转所代表对她的二元社会结果进行编码，以使人口旋转结构.自旋方向取决于外场（EF）和它们在网络中连接的其他自旋。与常规社会统计（对协变量具有线性依赖性的逻辑回归）一样，我们将EFs建模为Blau空间每个维度的线性场，其中Blau空间k每个维度的线性系数为hk，因此与EFs的单个自旋相互作用为标量积。自旋与EFs的相互作用仅取决于它们的坐标，因此它们倾向于与EFs对齐（见图2C）。

自旋构型的能量由哈密顿函数给出，

其中是Blau空间维度k中的EF线性系数，J是自旋相互作用和能量之间的比例因子，称为连接强度，是邻接矩阵。请注意，连接内核参数控制邻接矩阵A，使得核参数对哈密顿量的唯一贡献是通过A。此外，从哈密顿量来看，连接强度J和偏置项之间存在耦合在式2中的，这意味着在某些情况下这两个因素的不同组合可以产生相同的自旋构型；这将在下面的推理部分中讨论。我们可以添加一个同质场，整个群体都能感受到它，而不管它们的坐标如何。然而，在下面我们考虑的情况下，将设为零是合理的。组态概率由逆温度下的玻尔兹曼分布给出

以及归一化常数

是配分函数，其中和是所有可能的自旋构型，，对于伊辛模型，这是2^N项。构型概率表示在平衡状态下，系统处于配置状态的概率。图2D给出了一个自旋分配的示例，该分配是在特定网络结构（在本例中为特定连接性内核的SRGG）上额外生成的。至关重要的是，自旋并不完全由EFs或网络结构决定。

模型参数的推理方法

给出了社会结果的记录与总体Blau空间坐标zisin; ℝNtimes;K，我们的目标是推断模型参数. 对于伊辛模型，即使对于小系统，也无法计算配分函数Z，因为它需要计算2^N项。另一个挑战是，Z本身取决于模型参数，需要为每个可能的参数集重新计算。在这种情况下这种推断被称为双重难处理（34），马尔可夫链蒙特卡罗法具有挑战性。

作为一种替代的无似然方法（尽管如此，它避免了平均场近似），我们使用近似贝叶斯计算（ABC），它已被应用于具有难以解决的似然性的广泛问题（35,36）。在算法1中，我们展示了模型参数的基于拒绝的ABC推理方法。我们假设我们有先例关于可能的参数值。在第4行和第5行，自旋组态的生成需要两个步骤：（i）给定自旋坐标，从连接性核（等式2）生成SRGG，以及（ii）根据（i）中生成的图和（等式3）中的哈密顿量参数生成自旋组态。

我们使用Glauber动力学来生成自旋构型对于模型参数的任意组合来自玻尔兹曼分布。为了提高ABC拒绝算法的效率，我们定义了一组低维摘要统计。我们用向下（或向上）自旋的分数总结共享相同坐标，其中是Blau空间坐标z处的单个旋转数。当有C个不同的Blau空间坐标填充了自旋时，汇总统计数据将是（为了便于记法，也被表示为S）。为了使我们提出的方法成功，我们需要因此，我们用来近似我们的后验概率，在用函数总结它们之后使用来衡量与两者之间的差异. 我们定义了（原始社会结果数据的汇总统计）和（从中产生的自旋组态的观测数据)

是观测到的自旋数据中向下自旋的分数与产生的自旋之间的绝对差，因此只有当时，距离也可以被视为加权平均绝对误差（WMAE）。值得注意的是，我们的观测数据本身将在不同的小空间区域（例如，吸烟者或选民在不同小空间斑块中的比例）以自旋上升分数的形式进行聚合。因为我们正试图模拟我们的观测数据，并且假设所有具有相同坐标的自旋在统计上是不可区分的（Eq.3），至关重要的是， 是充分的统计，ABC后验概率趋向于精确的贝叶斯后验概率在极限。如果所有个体都可以获得连续的微观数据，则需要进行一些分类，利用我们的ABC推断对充分性进行相应的刻画。对于某些应用程序（如我们的投票示例中所示），可以通过重新调整中的连接性内核偏差项来重新调整总体大小在等式2（见文本S3）。最后，由于模型参数的ABC近似后验概率是通过独立样本获得的，因此可以直接将算法并行化，从而同时获得样本。对于更有效的抽样程序，也可以使用ABC的顺序抽样方案（37）。

结果

ABC推理可以从合成数据中估计模型参数

我们测试了ABC推理方法恢复合成快照数据的网络和行为过程的已知参数的能力。我们注意到，与其他逆伊辛或网络推断方法（38,39）不同，我们不寻求恢复唯一的网络链接，我们不观察每个自旋状态（仅粗略观察），我们也不使用时间序列数据（尽管有可能将模型扩展到重复观察；参见文本S2）。对于社会数据来说是合理的，我们假设我们可以获得关于个人社会坐标的信息。我们简单但合理的模型结构允许我们从由快照行为数据和普查信息组成的非常有限的数据集中提取信息。鉴于调查和普查人口统计变量通常是有序的或分类的，我们在实验中使用了有序数据和合成数据。我们在对应于有序自旋态的温度下（与无序自旋态相比，当系统处于“更热”状态时，没有显示整体磁化；见图S3），对两种不同的连接强度组合执行ABC抑制方法。我们发现在给定的温度下, 有一个值，连接的每对自旋对齐（因不同的值而改变）。这一现象对应于一个强的排列机制，其中相互作用项对哈密顿量的贡献主导着系统的动力学。因此，任何在自旋组态上都有类似的分布，其中连接的自旋是对齐的。我们在两种不同的合成数据场景中测试了我们的推理方法：一种是强连接强度，另一种是弱连接强度。

在图3中，我们展示了不同场景的ABC后验概率，和。我们在推理中设置了两个模型参数：x轴EF 和连接性偏差项关于，从等式4中，我们可以看到逆温度参数乘以线性EFs h；因此，在不违反任何约束的情况下，我们选择通过设置来减少一个自由度。关于连通性偏差项在等式2中，连接强度J和偏置项哈密顿量中的之间存在耦合（等式3）。这意味着在某些情况下，这两个因素的不同组合可以产生相同的自旋构型，自旋配置可能是低连接密度（）和强连接强

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[588145]，资料为PDF文档或Word文档，PDF文档可免费转换为Word