英语原文共 10 页,剩余内容已隐藏,支付完成后下载完整资料
耦合多芯光纤的
缠绕弯曲诱导型纤维的
绝热/非绝热超模式转型
Taiji Sakamoto, Takayoshi Mori, Masaki Wada, Takashi Yamamoto, Member, IEEE,
Fumihiko Yamamoto, and Kazuhide Nakajima
摘要——关于多芯光纤耦合的超级模式下功率传输特性的数值模拟和实验研究。我们发现,光纤的缠绕和弯曲通过绝热/非绝热过程造成的模式耦合,是不同于由于结构摄动(即微弯)引起的模式耦合的。我们还研究了双芯光纤耦合的脉冲响应特性,并且发现了有一个对于MIMO(多入多出技术处理)最小限度复杂性的优化芯距。最终,我们使用双芯光纤进行了4times;4多入多出技术传输实验来评估它们的传输特性。我们发现,即使当传输线有大的核心倚赖的增/损值时,强耦合多芯光纤也能够减少接受到信号之间的质量差。
关键字——差模时延,多芯光纤,多入多出技术,超级模式
1.简介
空间分割复用(SDM)使用多芯光纤(MCF)或少模光纤(FMF)技术深入研究的目标是大幅度提高传输容量。近些年,超过1 Pbit/s和1 Ebit/s·km的传输系统已经用多芯光纤实现了。空间密度对于多芯光纤是一个重要的参数,即每单位面积的芯数。我们注意到,由于芯间串扰,过小的多芯光纤芯距值会产生信号退化。因此,在空间密度和串扰之间要平衡。有着较小芯距的耦合多芯光纤已被提出比非耦合多芯光纤有着更高实现更高核心密度的可能性。不幸的是,耦合多芯光纤有着更高的芯间串扰,有可能导致严重的信号衰减。因此,多入多出技术处理被用在接收器上来弥补发生在光纤中的芯间串扰事故。在一个耦合多芯光纤的系统里,核间差模延迟(DMD)和多芯光纤的脉冲响应特性是直接影响多入多出技术处理复杂度的重要参数,正如基于少模光纤的系统的报告一样。正是这种强耦合的多芯光纤有着减少脉冲响应范围的优势,也就是脉冲响应宽度和长度的平方根成比例。然而,耦合机制在耦合多芯光线的光纤设计以及脉冲响应特性的关系中还有一些细节没有弄清。
在我们以前的工作中,我们的揭示纤维扭曲和弯曲的数值模拟和实验研究对于超级模式中的模式转换有着很大的影响。这篇论文中,我们调查了光纤设计对于脉冲响应传播的影响,并揭示了存在一个最佳芯距可以减少多入多出技术的处理。我们的论文有如下组成。第二节介绍了一个理想的光纤扭曲和弯曲引起的模式耦合的处理方法,并且向我们展示了模式耦合在弯曲半径和扭曲率上面的依赖性的数据结果。第三节介绍了关于模式耦合的双芯光纤的制作实验来证明我们用了基于波长扫描测量法来描述短双芯光纤的强模式耦合的仿真模型的有效性。第四节分析了双芯光纤数值模拟和实验研究的脉冲响应特性,并且阐明了怎样最小化脉冲响应扩散。最后,第五部分描述了强耦合双芯光纤4times;4传输实验的结果,并说明了使用强耦合多芯光纤就减少信号质量差异而言的优点,即使当传输线核心增益/损耗很大的时候。
2.多芯光纤耦合的光纤缠绕弯曲感应理论处理
光学光纤的脉冲响应必须设计得当,因为它和多入多出技术处理的复杂性密切相关。基本上,它是源自于核间差模延迟之间正交传播模式,每个模式的传播损耗,和它们之间的光纤的模式耦合。模式耦合理论表明,模式耦合可以引起结构的扰动,比如为弯曲或者核心轮廓的变化。耦合多芯光纤的基于扰动模式耦合的数值模拟的方法研究在相同的方式正如少模光纤。然而,多芯光纤和少模光纤的一个区别就是芯偏移。因此,应该考虑光纤扭曲和弯曲对模式耦合的影响。
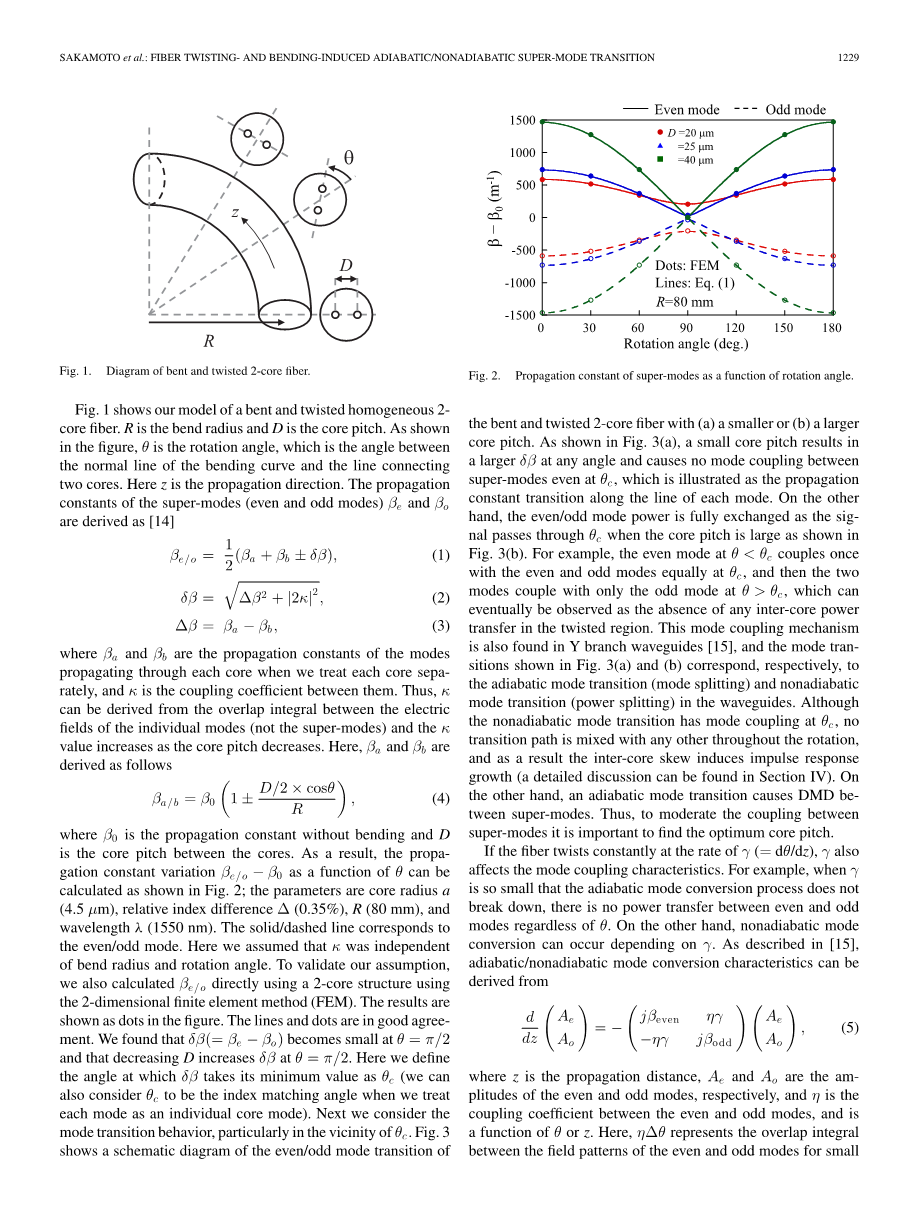
图一向我们展示了弯曲缠绕均匀的双芯光纤模型。R是弯曲半径,D是芯距。如图所示,theta;是旋转角度,是弯曲曲线和两芯的连接线的法线之间的夹角。这里的Z是传播方向,超级模式(甚至和奇数模式)的传播常量beta;e和beta;o由如下导出
beta;e/o =(1 /2)*(beta;a beta;b plusmn; delta;beta;) (1)
delta;beta; = (Delta;beta;^2 |2kappa;|^2)^(-2) (2)
Delta;beta; = beta;a – beta;b (3),
其中beta;a和beta;b是我们分别处理每一个芯的时候通过每一个芯的模式传播的传播常量,还有kappa;是它们之间的耦合系数。因此,kappa;可以从体模式的电场(不是超级模式)重叠部分的积分得到,并且kappa;的价值会随着芯距的减少而增加。这里,beta;a和beta;b由如下导出:
beta;a/b = beta;0(1 plusmn;(D/2 times; costheta;)/R) (4),
其中beta;0是非弯曲的传播常数,D是芯距。因此,传播常数beta;e/o - beta;0作为theta;的函数可以被计算出,如图二所示。参数是芯半径(4.5毫米)、相对折射率差Delta;(0.35%),R(80毫米),lambda;和波长(1550 纳米)。实线/虚线对应偶数/奇数模式。在这里,我们假设,kappa;是独立的弯曲半径和旋转角度。为了验证我们的假设,我们还直接使用双芯结构采用二维有限元法(FEM)计算beta;e/o。结果显示为图中的点。这些线和点有很好的一致性。我们发现在theta; = pi;/2的地方delta;beta;(= beta;e - beta;o)变小了,另外在theta; = pi;/2的地方D减小了delta;beta;增加了。这里我们定义一个角度,delta;beta; 取它的最小值theta;c (当我们把每一个模式作为每一个芯的模式的时候,我们还可以考虑theta;c是折射率匹配角度)。接下来我们考虑模式的转变行为,尤其是theta;c的附近。图3显示了偶数/奇数模式转换的弯曲缠绕双芯光纤的芯距较小的示意图(a)或芯距较大的示意图(b)。如图3(a)所示,芯距较小导致即使在theta;c产生一个较大的任意角度delta;beta;和超模之间产生的无模式耦合,这说明传输常数在每个模的线上传输。另一方面,偶数/奇数的功率当芯距较大是同时信号传输过theta;c时是完全交换的,如图3(b)。例如,在theta; lt; theta;c处的偶数模式曾经和偶数和奇数模式在theta;c处的相等,另外最终在缠绕的区域可以被观察作为缺乏任何核间的功率传输的两个模式耦合只在theta; gt; theta;c处的奇数模式。这一模式耦合机制也被发现在Y分支波导,另外模式转换对应如图3的(a)和(b)所示,分别在波导中为绝热模式转变(模式分配)和非绝热模式转换(功率分配)。虽然非绝热模式转换在theta;c处模式耦合,没有过度的路径混合在其他的整体循环中,因此,核间偏斜以脉冲响应的增加(详细的描述可以在第四节中找到)。另一方面,绝热模式转变导致了超级模式之间的核间模差延迟。因此,适度的超级模式之间的耦合对于找到最佳芯距非常重要。
如果光纤的缠绕率不断的在gamma; (= dtheta;/dz),gamma;也影响耦合特性。例如,当gamma;太小的时候,绝热模式转变过程中不分解,在偶数和奇数模式之间就没有功率转移无论theta;取何值。另一方面,非绝热模式转换可以取决于gamma;。如,绝热/非绝热模式转换特性可以由如下推出:
(5)
其中z是传输距离,Ae和Ae分别是偶数和奇数模式的振幅,另外eta;是偶数和奇数模式之间的耦合系数,还是theta;或z的函数。在这里,eta;Delta;theta;代表着重叠的奇数和偶数模式的场分布之间的积分来求小角度旋转Delta;theta;:
(6),
这里Ee/o是偶数/奇数模式的电场模式。我们以同样的方式介绍一个分析方法,以避免在二维模场计算上耗费时间。每个超级模式的电场被描述为个体芯模式的线性组合,如下:
Ee(x,y) = dEa(x,y) eEb(x,y) ,
Eo(x,y) = -eEa(x,y) dEb(x,y) (7).
这里,Ea/b(x,y)是个体芯模式的电场模式,还有:
e/d=2kappa;/(Delta;beta; delta;beta;) = f (8).
这就产生了
(9),
如附录1所述,以上两个公式(8)和(9)表明了f是一个表征为模式耦合的基本参数。模式耦合系数,eta;,随着模场的变化随光纤旋转而增加,因为f决定了超级模式的场模式。例如,小芯距多芯光纤的旋转模场模式的变化是渐进的(df/dtheta;很小),如图三(a)所示,模式转变遵循着绝热过程。
在之前的公式(5)中,采用1毫米的Delta;z(= Delta;theta;/gamma;)小步求解数值。图4显示了计算的功率耦合系数|eta;Delta;theta;2|作为在gamma; = 0.8 pi;和R = 80 厘米处theta;的函数。我们发现最大的模式转换发生在theta; = pi;/2,另外系数随着D降低而降低。40毫米的D的功率耦合系数峰值是-3dB,并且在theta;c的附近有两个耦合点,导致了超级模式功率的充分交换如图3所示。图5显示了偶数/奇数模式Pe/o在theta; = pi;的功率时的Pe(0) = 1和Po(0) = 0,这意味着偶数模式只有在theta;的值在从0到pi;的地方输入和弯曲的光纤处于激发。我们也表明了我们获得使用实际的gamma; = 0.8 pi;弯曲和缠绕的双芯光纤模式和二维光束传输方法(BPM),如图中所示的点。我们确认我们的计算模型使用公式(5)满足数值结果。对于一个D比较大的光纤,输入偶数模式功率在theta; = pi;/2处完全转化为奇数模式并且在theta; = 2pi;/3处变回偶数模式。这里我们定义的芯距Pe(pi;) = 0用来区域产生非绝热模式转换。因此,这种过渡群体延时特性跟随dbeta;a/dw。这说明了这两个转换的群延迟的正弦可能变化,并且平均群延迟超过是同为双芯如果多芯光纤的芯是相同的。相反,一个D小的光纤有着可以忽视的模式耦合不管缠绕由于Pe(pi;) = 1,这被称为绝热模式转换。一个确定的芯距设计(大约D = 20 sim; 25 毫米,尽管在这个案例中它取决于gamma;)在间隔为pi;/gamma;时有着混合的绝热和非绝热周期的模式转化,另外脉冲响应传播距离(公里)以平方根比例增长由于随机模式置乱。图5(b)显示了模式耦合取决于曲率半径。我们发现曲率半径也极大的影响了耦合程度,并且突然/渐变弯曲加强了非绝热/绝热的转化过程。这证实了我们的假设,耦合多芯光纤的模式耦合受多芯光纤的扭曲率和曲率半径很大的影响。
最后,我们计算三芯光纤的模式耦合作为例子来探讨我们提出的模型对于超过两个芯的多芯光纤的适用性。我们假设在多芯光纤设计描述和计算它的模式耦合特性。图6显示了一个横截面的图像和三芯光纤的模式转换的例子。图中有三个空间的超级模式,按有效指数降序定义他们的模式阶数。我们发现,类似于超级模式区域时可以观察到垂直对齐的曲面两个芯(这里theta; = pi;/6)。图7(a),显示了作为旋转角函数的超级模式之间的传播常数和串扰。我们利用公式(6)进行了一个Delta;theta; = 1度的二维模式场的计算得到了eta;Delta;theta;。这三种模式中的两种在theta;c = pi;/6 times; (2n - 1)处互相耦合在一起,其中n是整数。图7(b)显示了基于二维光束传输方法的计算在三芯光纤超级模式之间的串扰值。这里,我们定义串扰值作为光纤扭曲部分之后输入超级模式和其他超级模式之间的输出功率比。虽然串扰值随着扭率的减小会每增加一个旋转,没单位长度的串扰值约为-22dB并且几乎独立于gamma;,因此我们可以预期获得足够的模式置乱。对于4芯以上的多芯光纤,我们可以通过解决在多芯光纤所有超级模式场模式用二维光束传输方法或者公式(6)计算出来模式耦合特性。
<!--
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[140589],资料为PDF文档或Word文档,PDF文档可免费转换为Word
课题毕业论文、外文翻译、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。