
英语原文共 2 页,剩余内容已隐藏,支付完成后下载完整资料
TM10-2 sice02-0480
基于神经网络的非线性PID控制系统设计
Y.Ohnishi1,T.Yamamoto2,T.Yamada3,I.Nanno3,M.Tanaka3
1.日本广岛黑原国立理工学院, 2-2-11,Aga Minami,Kure Hiroshima
2广岛大学,1-1-1 Kagamiyama,Higashihihiiroshima,日本
3欧姆龙公司,2075 Miyoshi,Okayama,日本
摘要:基于经典控制理论的PID控制方案长期以来广泛应用于各种过程控制系统。然而,由于这类过程具有非线性特性,因此很难确定“最优”PID参数。本文提出了一种基于神经网络的系统辨识方案。在此基础上,提出了一种基于估计的PID控制方案。根据新提出的方案,首先用神经网络对系统参数进行估计。利用神经网络产生的估计值计算PID控制参数。该方法可用于非线性系统的PID控制。最后,以数值模拟为例,对新提出的控制方案的性能进行了研究。
关键词:系统辨识、神经网络、PID控制
1、引言
基于经典控制理论的PID控制方案长期以来广泛应用于各种过程控制系统中。这主要是因为PID控制器具有简单的控制结构。然而,由于这类过程由于建模误差和过程中的波动而具有非线性特性和不确定性,因此很难确定“最优的”PID参数。
另一方面,神经网络在非线性系统中的有效性已经讨论过了。特别的是,提出了一些利用神经网络的控制方案(Rumelhart等人,1987年Gupta和Rao,1993年)。
本文利用神经网络进行系统辨识。即利用神经网络对系统参数进行估计。将估计值转化为时间常数、系统增益和时滞。基于这些参数,在线确定PID参数。根据新提出的方案,对PID参数进行了相应的非线性调整。最后,通过仿真实例,对新方案的有效性进行了数值评价。
2.基于神经网络的系统估计器
考虑一个单输入单输出系统,用如下非线性离散时间模型描述:
其中u和y表示控制输入信号矢量和相应的输出信号矢量,由下式给出:
此外,k表示延时,G表示非线性函数。
本文提出了一种基于神经网络的参数估计方法。首先,介绍了以下识别模型:
其中,km表示估计延时的最小值。
本文构造了图1所示的神经网络用于参数估计。注意,神经网络输出层中的每个单元都对应于估计参数。神经网络中包含的权重因子根据反向传播方法进行更新,其成本函数e由以下公式给出:
根据估计值,时间常数t、系统增益k0和延时L的计算公式如下:
输入
输出
隐藏
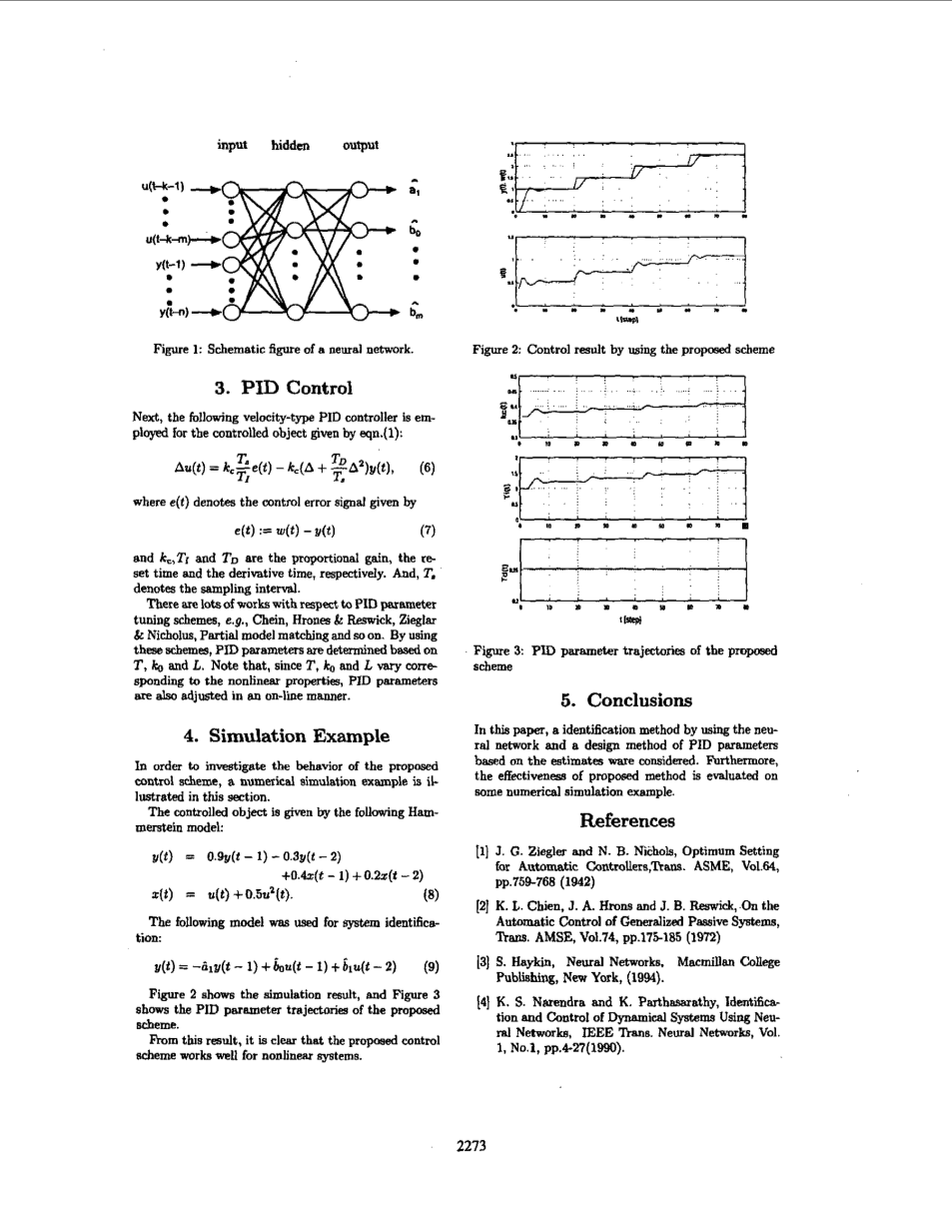
图1:神经网络的示意图。
3.PID控制
其次,对(1)给出的被控对象采用以下速度型PID控制器:
其中e(t)表示由
kc、tl和td分别是比例增益、复位时间和微分时间。ts表示采样间隔。在PID参数整定方案方面有很多工作,例如Chein、Hrones amp; Reswick、Ziegars amp; Nicholus。部分模型匹配等。利用这些方案,根据T、k0和L确定PID参数,注意,由于T、k0和L随非线性特性的变化而变化,因此PID参数也可以在线调整。
4.仿真示例
为了研究所提出的控制方案的性能,本节给出了一个数值模拟实例。
控制对象由以下Hammerstein模型给出:
以下模型用于系统识别:
仿真结果如图2所示,PID参数轨迹如图3所示。
由此可知,该控制方案对非线性系统的控制效果良好。
图2:使用提议方案的控制结果
图3拟用方案PID参数轨迹
5、结论
本文提出了一种基于神经网络的辨识方法和基于估计的PID参数设计方法。并通过数值模拟实例对该方法的有效性进行了评价。
6、参考文献
[I] J. G. Ziegler and N. B. Nichols, 《自动控制器的最佳设置》, Trans. ASME, Vo1.64, pp.759-768 (1942)
[2] K.L. Chien, J. A. Hrons and J. B. Reswick, 《关于广义被动系统的自动控制》, Trans. AMSE, Vo1.74, pp.175-185 (1972)
[3] K. S. Narendra and K. Parthasarathy, 《利用神经网络识别和控制动力系统》. IEEE Trans. Neural Networks, Vol. 1. No.1, pp.4-27(1990).
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[20668],资料为PDF文档或Word文档,PDF文档可免费转换为Word
课题毕业论文、外文翻译、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


