英语原文共 7 页,剩余内容已隐藏,支付完成后下载完整资料
有效折射率的性质分析
R.S.普齐科,A.M.麦泽金
摘要:根据有效参数考虑平面波通过周期性分层系统的传播。 讨论引入有效参数的问题。 已经证明,虽然不能引入有效导纳,但是可以引入当系统尺寸增大时趋向于值的有效折射率。 结果表明,有效波矢量导数是频率的分析函数。 特别地,获得了有效波矢量导数的实部和虚部的样关系。 还考虑了有效折射率的样关系。 在数值上获得的结果通过在“等阻抗”系统的特定情况下的麦克斯韦方程的精确解来证明。
关键词:均质化,分层结构,有效介质,有效参数,关系电磁参数检索。
- 介绍
在长波近似中,用均匀介质代替不均匀复合材料是很方便的,其中,电磁性由局部电磁场的平均值产生。这种方法通常称为均质化程序。
然而,在一些特殊情况下,常规有效参数 - 介电常数和磁导率的引
可能看起来物理上不正确。例如,对于周期性分层样本,使用的有效参数和 [1-7]会导致矛盾[8-12]。让我们考虑由偶数层组成的有限周期性样本(其单位单元由两个层组成)(见图1)。在样品中,第一层和最后一层由不同的材料制成。因此,样品相对于光入射方向的反转是不对称的[8];即使在无损情况下,从右()和从左()入射的波的反射系数的相位不同
然而,对于均匀层,相应应相同。 计算直接表明和的差值是d /lambda;的一阶,其中lambda;是波长,d是单层的厚度。因此,在 和 方面的分层系统的均匀化程序仅在静态情况下是正确的(lambda;=infin;)[8]。
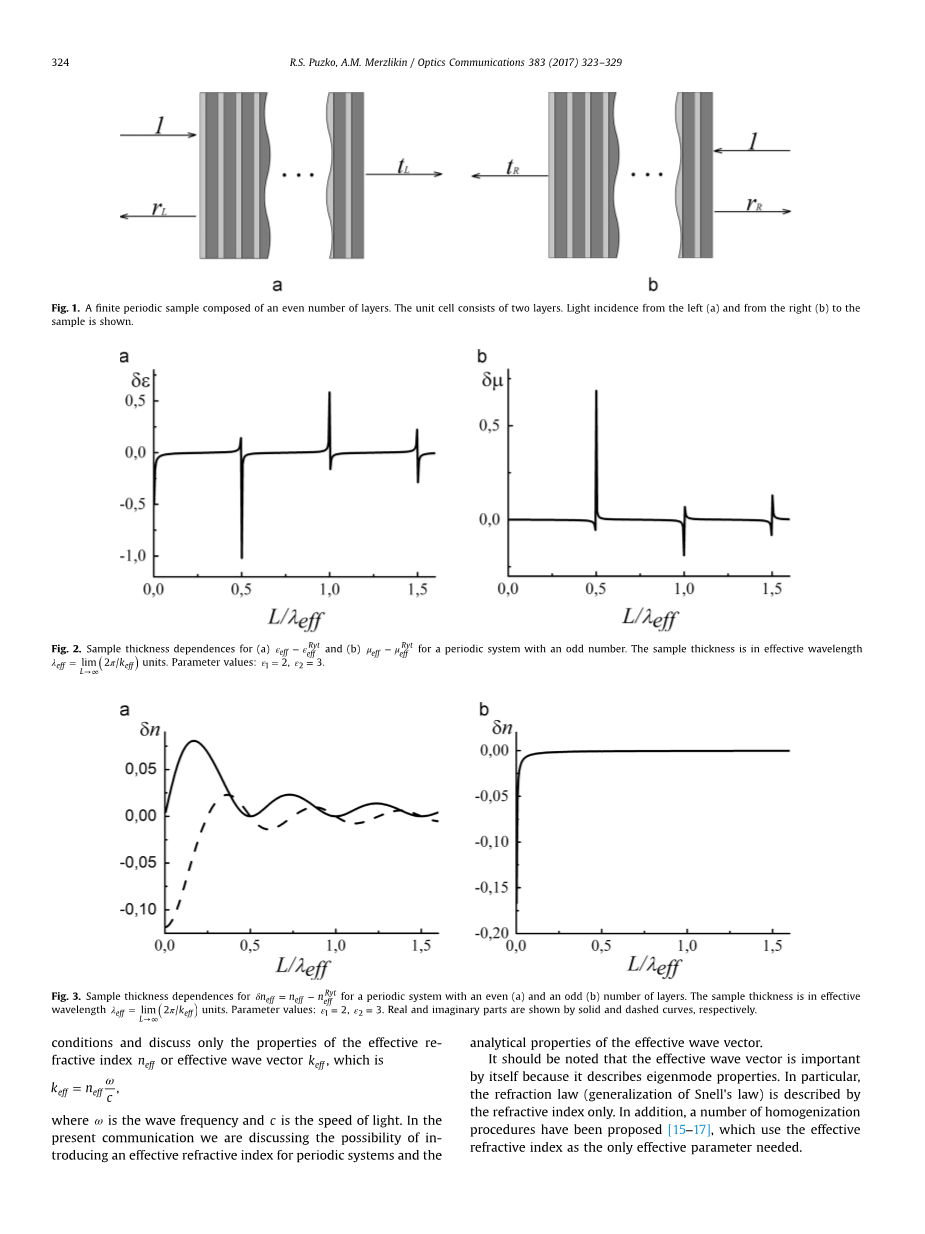
对于由奇数层组成的样本,在[8,9]中证明了有效参数对样本大小的依赖性。图。图2显示了对于由奇数层组成的有限样本和参数检索的参数之间的差异。随着系统尺寸的增加,出现在某些点的峰不会消失。因此,检索的参数描述样品而不是一些均质材料。
尽管和不能被正确地引入超过静态近似的事实,可以引入有效折射率。长波近似中的计算表明,随着层数的增加,有效波矢量(从散射参数检索)趋向于由预测的常数[8-11]。来自[9]的图3示出了有效折射率对无限大小预测的值的收敛。
引入超过静态近似的有效参数的问题被简化为两个独立的问题:有效折射率的定义和边界条件的描述。以前,借助于附加表面电流[13]或边界上的附加有效层[14]的有效阻抗的正则化被认为是固定边界条件问题的方法。然而,这个问题还远远没有得到解决。
现在我们将远离边界条件的问题,并且仅讨论有效折射率或有效波矢量的性质,
其中omega;是波频率,c是光速。 在本通信中,我们讨论了为周期性系统引入有效折射率的可能性以及有效波矢量的分析性质。
应当注意,有效波矢量是重要的因为它描述了本征模属性。 特别地,折射定律(斯涅耳定律的一般化)仅由折射率描述。 此外,已经提出了许多均匀化程序[15-17],其使用有效折射率作为所需的唯一有效参数。
图 1.由偶数层组成的有限周期性采样。 单元电池由两层组成。 显示了从左(a)和从右(b)到样品的光入射。
图2.对于具有奇数的周期性系统,(a)和(b)的样品厚度依赖性。 样品厚度为有效波长效应单位, 参数值:ε1= 2,ε2= 3。
图3.对于具有偶数(a)和奇数(b)数量的层的周期性系统,样品厚度依赖性为 。样品厚度为有效效应
波长单位,参数值:ε1= 2,ε2= 3。实部和虚部分别用实线和虚线曲线表示。
2.有效波矢
让我们考虑电磁平面波通过无限周期分层系统(波垂直于层)的传播,其单位单元由两层组成。 第一层的特征在于介电常数和磁导率ε1和mu;1以及厚度d1; 第二层的特征在于类似的参数ε2,mu;2和d2。
该系统的本征态是Bloch波,其参数由 [3]找到,并由分散方程描述:
(1)
其中Y1和Y2是相应层的导纳,rho;1和rho;2是它们的光学长度。
(2)
(3)
k=omega;/c是自由空间的波矢。色散方程 定义Bloch波矢量,其可以被解释在样品前面和后面的电磁场,作为无限分层系统中的有效波矢量。
现在让我们考虑由有限数量的层组成的周期性结构。 可以通过透射系数来定义有效波矢量。 传输系数可以表示为:
(4)
通过异质结构的波传播可以被视为通过孔材料表面的三级过程传输,在结构内部的传播以及通过材料 - 真空表面的传输(参见图4)。
传播的第一阶段和最后阶段可以通过一些有效的边界条件来表征(在阻力方面[8,9,18]或者更复杂[13,14])。尽管有效边界条件可能取决于系统的厚度,边界效应对传输系数(作为周期或准周期函数[8])的贡献不随着厚度的增加而增长。相反,第二级(通过结构的传播)进入透射系数的贡献随着系统的长度而增长:固有解的复相(相的主要部分由吸收或不相干散射)随着系统的厚度L线性(平均)地增长。因此,可以忽略表面效应,并且将透明系数的对数的虚部视为相位侵入,
图4. 通过传播复合材料的平面波。
样品的长度L.对数ln(t)/ L的实部描述了电场振幅的减小,其由波矢量的虚部表征。因此,对于足够厚的结构的有效波矢量可以定义如下:
(5)
(6)
或组合在一式后
(7)
传递矩阵(T矩阵)描述了样本前面和后面的电磁场之间的关系
(8)
其中TEH是场表示中的传递矩阵。 还可以引入T矩阵,其连接在不同方向上传播的波的幅度
(9)
其中TAB是波表示中的传递矩阵,系数A1和A2分别是沿着样本前面和后面的轴传播的波的幅度,B1和B2是波的幅度,在相反的方向。
通过考虑层两侧的边界条件,可以获得同质层的T矩阵的显式形式。 波形表示中的传递矩阵具有形式
(10)
其中是层的光学长度,是其导纳。 分层系统的T矩阵可以通过以相反顺序乘以层的T矩阵来获得
T=prod;Tj. (11)
同时,可以表示系统的T矩阵根据反射的振幅系数(系数和,用于从系统相对侧的 入射)和透射传递(不依赖于方向)
(12)
表示(12)允许以T矩阵元素表示传播系数。 然后,可以获得有效波矢量(7)。
当系统增加时,该有效波矢量应当趋向于的值。的波矢量的实部的行为可以通过线性依赖近似。显着偏差仅出现在带隙附近。 在带隙内部,波矢量的实部是恒定的,并且虚部在带隙的中间具有一个最大值。
数值计算的结果表明由(7)定义的有效波矢量与的波矢量(参见(1))的点向连接。图5a示出了由4,10和100层组成的结构与真实的的实部的偏差
的一部分。 如图所示,最大偏差在频带内间隙。 然而,随着层数的增加,有限样本的色散曲线趋向于的色散曲线。
图5.由4(黑色曲线),10(灰色曲线)和100(光效)组成的结构的有效波矢量的偏差的实部(a)和虚部灰色曲线)层从的波矢量。 层的介电常数ε1 = 2和ε2 = 3。
图6.对于100层有限结构(黑色曲线)和系统(灰色曲线)的情况,有效波矢量导数的实部(a)和虚部(b)。 层的电磁参数与图1中的相同。
图 7. 的波矢量的导数与从KKLR获得的值之间的差。 在计算中使用的积分步骤的依赖关系以对数标度显示。 针对差的实部(a)和虚部(b)的范数L1计算量。
图8. 有效折射率与从(28)和(29)获得的值的相关性的相对偏差。 图形给出了实部(a)和虚部(b)。 系统,具有两种类型的层:ε1= 5,mu;1= 3,d1 = 0.25和ε2= 2,mu;2= 1,d2 = 0.1。
对于有限系统(4,10和100层),的虚部与的虚部的偏差示于图5b。 对应于4层样品的黑色曲线类似于色散曲线; 然而,虚部甚至在带隙外部也是非零的。 随着层数的增加,吸收带的变窄变得明显。 曲线在的情况下收敛到依赖性。
当然,导数也趋向于,然而,该收敛不是均匀收敛。 图2中的黑色和灰色曲线。图 6显示有限厚度样本和的波矢量的依赖性。可以看出,均匀收敛的违反发生在带隙的末端。
3.有效波矢导数的分析性质
我们的论文中的关键点是验证式的关系,
(13)
(14)
应满足这些关系的建议是基于透射系数的分析性的想法。 单层(10)的T矩阵元素是频率的分析函数。 因此,整个系统(11)的T矩阵元素也是频率的分析函数。 一旦透射系数t可以用T矩阵元素(12)表示,它也是频率的分析函数。 对于的导数,适用以下公式:
(15)
可以看出,对于分层系统的的导数应该满足KKLR作为分析函数。
为了验证有效波矢量导数的KKLR,我们使用数值方法(见图7)。 积分(13)和(14)的计算使用梯形法进行。 它允许我们将误差减少到积分步骤的二阶。值得一提的是,关系式(13)和(14)中的被积函数在点omega;0处具有奇异点。 因此,应特别注意在杆附近的集成。 计算(13)和(14)中的主积分值,我们使用近似的被积式。 令被积函数中的分数的分子f1和f0在点x =omega;0plusmn;h,其中h是综合的步骤。然后,通过建议分数的分子是线性函数f(omega;)= (f1-f0)(omega;-2h)/2h 0.5(f 1 f0),一个获得沿着域xisin;(omega;0-h;omega;0 h)的积分的结果,其等于f1-f0。
KKLR包含主积分值。 因此,应进行初步计算以选择数值算法的积分间隔。
我们通过在数值计算中应用任意精度的库来进行一组计算[19],以确保获得的结果不是数值错误的产物。
计算得到的第一个重要结果是KKLR(13)和(14)中的常数。 发现常数in公式(14)为,part;k/part;omega;的常数为。
4.磁性材料和吸收材料
在前面的部分中,我们得到满足KKLR的有效波矢量的实部和虚部
其中括号... 表示对复合样本长度的平均。 先前考虑的关系仅针对没有频率色散的非磁性,非吸收材料的情况进行研究。
在磁性和/或吸收材料的情况下,出现关于KKLR的有效波矢量导数的问题。 为了回答这个问题,我们考虑具有介电常数和磁导率的分层系统的模型,其满足在系统的任何点处的关系ε(omega;,x)=alpha;mu;(omega;,x)(alpha;不依赖于坐标, 频率)。 所考虑的结构不反射光:系统的任何点处的导纳是Y =radic;alpha;。 因此,通过在与系统的轴垂直的任何平面处应用场边界条件,可以看出系统中不存在反射。 我们可以写出用于波的麦克斯韦方程组的系统,该系统正常地传播到层(沿着系统的轴x)光的速度取为等于1
(16)
通过关系ε(omega;,x)=alpha;mu;(omega;,x),可以得到(从函数E(omega;,x)和H(omega;,x)到函数E(omega;,x)plusmn;alpha;H(omega;,x)的变换是有用的。 电场具有以下形式
(17)
因此,有效波矢的导数是
(符号lt;...gt; L表示在结构的长度上的平均值)。 通过重写这个公式为真实和虚部分和的导数,得到(对于简单的目的,我们假设系数alpha;是真实的)
(18)
(19)
其中,符号的Re(ε(X,omega;))= ε (X,omega;)和IM(ε(X,omega;))= ε Prime;(X,omega;)拍摄的。应用克拉默斯-克勒尼希关系为电子商之后(X,omega;)。
(20)
(21)
(22)
(23)
(22)
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[26119],资料为PDF文档或Word文档,PDF文档可免费转换为Word
课题毕业论文、外文翻译、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。