中纬度中尺度大气的动力机制外文翻译资料

英语原文共 8 页，剩余内容已隐藏，支付完成后下载完整资料

中纬度中尺度大气的动力机制

摘要：中尺度天气现象具有复杂的多样性，从而不能进行简单的分类。本研究中基于中纬度春季大范围内的云可分辨模拟进行了全时空的谱分析。在天气尺度上动能最大，而在中尺度上动能局限于“平流带”，其中空间和时间尺度通过速度尺度为10的比例常数相关联。通过计算控制方程中不同项的相对大小，可以识别五种运动状态。这些状态被分为准地转流，传播的重力波、与地形、声学模式和弱温度梯度相关的静止重力波，其中垂直运动受非绝热加热强迫。

1. 引言

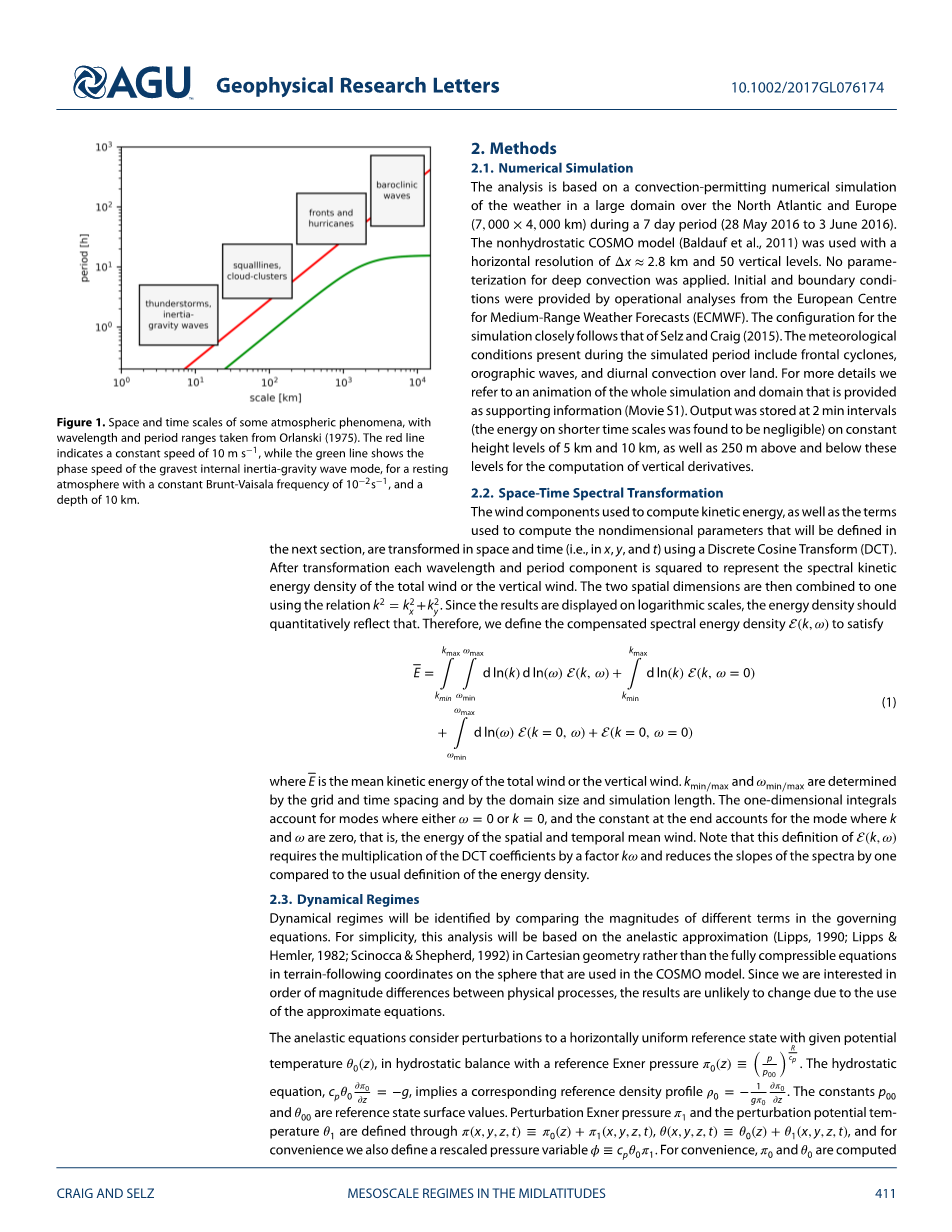
中尺度通过其不具备的特性进行定义。它不是天气尺度，即：空间尺度~1000km，时间尺度1天，运动满足准地转运动。它不是接近均匀和各方向同性的三维湍流尺度，其中空间尺度约100m，时间尺度为1分钟。相反，中尺度被定义在它们之间，并被分为了三个量级(Orlanski,1975)，并且包涵多种如雷暴、地形波、锋面、飑线中尺度对流系统和飓风的中尺度天气现象(图1)。这个定义并不通用，例如，人们可能会区分中尺度对流结构和孤立对流单体，通过他们不同的对流机制而提出问题。图1的一个显著特点是中尺度天气系统并没有囊括整个两个尺度之间的全部时空范围，但是它重点集中到了波长周期图的对角线上，其中对应着几米每秒的固定速度。这种速度有传输非线性平流的特征，尽管如垂直波长约为一公里的对流层重力惯性波也在这些尺度上发生。

在动能谱中，中尺度天气现象展示了不同的情况。在较小的尺度上，观测和数值模拟约有的幂率，而在几百公里尺度上转为。这样能量分布背后的物理机制并不完全清楚(e.g., Bierdel et al., 2016; Blazica et al., 2013; Skamarock et al., 2014)。在大尺度上的异常的大值可能是由于准地转湍流造成的涡街。这个理论适用于气流满足准地转平衡的天气尺度，然而对于较小尺度还未发现类似的平衡，或许是由于中尺度的天气现象并不能用一个简单的理论进行解释。

本文通过试图通过计算中尺度主要的动力平衡中各项对能量谱的贡献来对来给这些问题提出新见解。这个分析是初步的，但是包含两个创新点：首先，使用全时空的谱分解。这系列的分析曾经被Wheeler and Kiladis(1999)成功地应用于识别热带波动模式，但在本次研究中这种方法将被普遍应用；其次，将会重新估计无量纲数，例如，罗斯贝数，并将其与方程中其它项进行比较，从而从时间和空间的角度确定动力机制。

图1 部分大气现象的时空尺度，波长和周期取自Orlanski(1975)。红色等值线表示10()，绿色等值线表示在有恒定的Brunt—Vaisala频率，深度为10km的静止大气中，大气内部最重要的惯性—重力波模式的相速度

1. 方法
   1. 数值模拟

分析基于在北大西洋和欧洲的大范围（7000m*4000m）的云可分辨数值模拟，时间范围是七天（2016年5月28日至2016年6月3日）。使用了非静力的COSMO模式（Baldauf et al.,2011），水平分辨率为2.8km，垂直有50个层次。没有使用深对流的参数化。初始边界条件由欧洲中期天气预报中心（ECMWF）提供。模拟的设置和Selz and Craig(2015)相似。模拟期间的天气条件包括锋面气旋、地形波和陆面的日对流。对于更多的细节，我们提供了支持信息（影像S1），这个影像可以提供整个过程的仿真动画。对于计算结果，在五千米和十千米的高度层上，保存每两分钟的输出结果（较短时间尺度上的能量忽略），在计算垂直方向上的导数的时候利用了各层次上下的250米的信息。

• 1. 时空的谱变换

被用来计算动能的风的分量，以及下一节被用来计算无量纲参数的项被是用离散余弦变换（DCT）的方法在空间和时间（即，x、y和t）进行变换得到的。在变换后每个波长和周期分量的平方被用来表示全风速和垂直风速的谱动能密度。然后利用将两个空间维度组合为一个维度。通过对结果的对数显示，能量密度可以定量地显示结果。因此，我们定义补偿谱能量密度去满足当为全风速和垂直风的总动能的区域。和被格点和时间间隔决定，同时也被整个区域的尺度和模拟时长决定。在=0或者k=0的情况下进行一维积分，而=0或者k=0的情况下始终不进行积分。注：对的定义需要DCT的系数和因子k的乘积，并且减小谱的斜率，使之与普遍定义的能量密度的斜率相同。

• 1. 动力机制

通过比较控制方程中不同项的相对大小，可以揭示动力机制。简单地说，这次分析将会基于笛卡尔几何中的滞弹性近似（Lipps,1990; Lipps amp; Hemler,1982; Scinocca amp; Shepherd,1992）,而不是COSMO模型中的地形跟随坐标中完全可压缩方程。因为我们的关注点在物理过程间的数量级的差异，所以近似解的存在导致结果不容易产生差异。

滞弹性方程考虑了相对于水平均匀状态下的给定位温的扰动，在静力平衡有一个参考Exner 压力，即。由静力学方程,可知密度分布。其中固定不变的和表示了地面的数值。扰动Exner气压和扰动位温由等式和确定，同时为了准确性，我们也重新定义了气压变量。方便起见，和由每步的水平均值确定，并且不是保持随时间严格的不变。综上，滞弹性方程组为

其中的变量u指的是三维风，v指的是水平风，f为地转参数。非绝热位温的源为,其中q是单位质量的加热率（J）。用无量纲参数去计算动力机制，而动力机制是被下面等式中的各项的相对大小所定义的。

在得出结果之后，其中的物理机制会在3.2部分被讨论。在空间网格上使用二阶有限差分计算每个项的贡献（在各自量级上）。实验应用实验的条件为水平格距，垂直层距离时间步长为。

图2 图(a)表示10km处的总动能密度的时空谱，图(b)表示5km处的垂直动能密度的时空谱，如方程(1)定义。上方和右侧的色标代表着不同的模态，右侧色标代表波长为无限时，上方色标则代表时间无限的情况。阴影区表示接近网格长度的空间模式，即。上方的虚线（对角线）表示10的典型的平流速度，而下方的虚线表示深层次的水平传播的重力波的频散关系。

图3 类似于图2的时空诊断图，但显示了在5km高度上的无量纲参数(6)—(9)的大小

上面所介绍的每个波长和周期的谱分解计算得出的比值，即为所求的参数。通过这种方法我们可以得到每个无量纲参数的波长周期。值得注意的是：不像动能密度，无量纲参数不能通过对数坐标轴显示方式进行修正，因为计算比值的时候该效果被抵消了。

1. 结论
   1. 动能

图2a展示了在对流层上层(10km)的动能的时空谱（5km处的时空谱与之相似）。天气尺度的作用在这一层起到主要贡献。空间波如果小于5的长度，它就不能被模式很好的解析，并且能量也因为频散而减少。这些情况通过填色或者灰色阴影在图中做了参考标记。在图中的右下角几乎找不到能量，同时在这个时空尺度对应的速度比深层次的对流层重力惯性波对应的速度更快。在中尺度的情况下，最大能量沿着对角线分布，为10。在图中的这个区域被称为平流带。

天气尺度的流场以涡旋运动为主，但对于中尺度这个结论尚不明确。在考虑对流层中层的垂直风的能量的时候，我们可以发现辐散的存在（图2b）。最大的能量的波长出现在波长为10km和周期约0.5h处，这种情况一般被认为是对流云不能被模式有限的分辨率所识别。即使在模拟长度所允许的最长周期内，最高分辨率的空间尺度上也有很大的能量，说明其中存在小尺度准静止的特征，如地形重力波。第二，垂直能量的增量沿对角线逐渐变弱，在天气尺度上时该能量变得不显著。最后，正如预期，在中尺度所有波长范围中，垂直动能的最大值在24h中的日周期中。相比之下，在日周期中水平动能只在有限波长中可见，与区域平均值的变化对应（图2a）。对于在不同物理过程中，无量纲参数对光谱的相对贡献将会在下一节讨论，其中对于无量纲参数的定义在2.3节。

图4第3.3节所定义的时空图：(qg)为准地转状态，(ac)声波，(adv)平流状态，(pgw)传播的重力波，(ogw)地形重力波。具体内容见正文。

• 1. 主要的平衡

罗斯贝数（方程 6）表示了惯性加速度和科里奥利加速度的相对大小。当罗斯贝数1时，科里奥利力起主要作用，流场接近地转平衡。图3a表示对于波长≳500km和周期T≳的情况下罗斯贝数为1或者更小时的情况。在天气尺度，即≳500km和T≳，流场为地转平衡，罗斯贝数约为0.2。参考时间和空间的阀值，罗斯贝数的低值区被定义为矩形，但是沿着平流的对角线有数值减小的趋势，可能是由于水平的风速比较大。

在被定义的矩形中，静力平衡的区域被波长和周期的阀值定义(方程 7)，这由惯性力和垂直压力梯度的比值计算得到(如图3b)，图中表示了在所有空间分辨率和时间尺度上≲1时的情况，以及≳30km和T≳0.5h时的lt;0.1的情况。如果以横纵比为基础，这种空间尺度就是合理的，因为垂直运动受到对流层深度的限制。

Strouhal数（等式 8）是欧拉和扰动位温的平流变化之比。St意味着一个未知的数量变化是在平流的时间尺度上发生的。图3c表示了天气尺度和平流带的情况，因此证明其合理性。大值的St表示平流项是小项，控制方程中主要是线性项的相互平衡。而对于对流层的深对流中的惯性重力波，图示的颜色分布也是正确的。在平流对角线上，缓慢运动对应的St是小值。这个结果符合预期，例如对于准静止的地形重力波，它与参考框架中的慢速的大尺度流场都是线性的。

Froude数的平方（等式 9）将位温的扰动量的拉格朗日变率与参考状态梯度的垂直平流进行比较。对于这个数与标准定义的Froude数的关系，也就是文中平流场与物体的相互作用的定义，将会在未来的工作中进一步讨论。在这里我们先把重点放在等式(9)对其的直接定义。对于重力波，其回复力来自于层结的重力波，是有序的并且一致。图3有两个区域出现了这种情况。首先沿着对流层深层的惯性重力波的分布曲线的颜色，其次是对于小尺度的准静止运动。对于准地转运动，的数值是最大的，但是它还是略小于天气尺度情况下。图中右下角的的最大值可能没有物理意义，因为这个尺度下有很少的能量。

Fr的最小值出现在中尺度对流带中，这其中有有趣的物理含义。Klein(2010)对中纬度进行了一般的尺度分析，指出小的Fr导致了位温的垂直平流和非绝热加热之间的主要平衡。也就是说，上升运动和绝热冷却是对热源的直接响应，因此水平温度梯度始终是弱的。这有点类似于弱的温度梯度(WTG)，这点越来越多地被应用于分析热带动力学（Raymond amp; Zeng, 2005; Sobel amp; Bretherton, 2000）。图3d表明这种平衡的原理也适用于中纬度中尺度天气。然而小的值约为0.5，因此在天气尺度上弱的温度梯度平衡不如地转平衡准确。

图5 (a) 10km处的动能和五个动力机制的贡献。两条斜率分别为2和2/3的黑线作为参考。(b)表示5km处的垂直动能，以及五个动力机制分别的贡献。(c)表示10km处的散度风和旋度风的动能。(d)表示5km处和在对流系统中的垂直动能。灰色阴影表示波长小于5的区域

• 1. 动力机制

前一节的研究结果可以用状态图（图4）概括，根据无量纲参数的大小和顺序统一的来定义。定义了五种机制。

1. 准地转(qg)：lt;0.5
2. 对流(adv)：gt;0.5和
3. 声波(ac)：gt;0.5和
4. 传播的重力惯性波(pgw)：gt;0.5，0.75lt;和Stgt;1
5. 准静止的地形重力惯性波(ogw)：gt;0.5，0.75lt;和Stlt;1

图5a表示了10km高度处的动能谱，显示了五种情况分别的贡献。这个能量谱主要受准地转运动和中尺度对流所控制。在小尺度上，地形波贡献了总能量的三分之一。有趣的是，通常情况下的能量谱的中尺度断裂，即，对于波长小于200km的波存在能量的低值区，不与这个形势一致。这说明与大幅降尺度地转运动湍流相关的准二维运动可能也有扰动位温造成的小对流，因此具有小的。在这次诊断中它们没能与潜热导致的直接强迫运动区分开来。

一个有趣的区别是散度风和旋度风的贡献。之前学者的研究发现(Bierdel et al., 2016; Blazica et al., 2013; Skamarock et al., 2014)，旋度风主要发生在大尺度，而散度风在较小尺度的谱中有与之相当的大小(图5c)。通过再次考虑5km处的动能的垂直分量(图5b)可以发现这个结论，因为对流层中层的垂直运动与高层的辐散风相关。而对于波长刚好超过10km的波长来说，这个数量级就很大，对于波长大于等于100km的波将减小一个数量级。大部分能量在平流区，但其中地形起到的贡献与波长小于50km的波贡献相当。在平流区的非绝热强迫可以被WTG的近似值所表示垂直运动的动能定量计算，即，以及它的余项。图5d显示了WTG的近似垂直风在对流区对垂直风的贡献，尤其是在长波的区域。

风场可以通过每个情况下的DCT变换进行逆变换来分解。作为支持信息(影像S2)，小区域24h的动画显示了小区域中五种机制下5km出的反演垂直速度。

1. 讨论

利用数值模式的输出结果，对整个中尺度的时空谱进行了分析。动能谱主要由平流带控制，其中对空间尺度和时间尺度做比，对应着大约为10的速度尺度。对流层中层的垂直运动在最小的空间尺度(10km—20km)和一小时或者更短的

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[17830]，资料为PDF文档或Word文档，PDF文档可免费转换为Word