交互式多目标优化的抓斗位移卸载起重机外文翻译资料

英语原文共 7 页，剩余内容已隐藏，支付完成后下载完整资料

交互式多目标优化的抓斗位移卸载起重机

摘要：在本文中，多目标优化（MOO）应用于最优的控制抓斗位移卸载起重机的问题。 起重机被建模为具有可变的绳长度和抓斗的轨迹受到船，码头，和起重机结构影响的车-摆系统。 最小化的目标被选择为时间，能量和最大瞬时功率。 最优控制问题直接同步最优解控制方法。 研究表明，MOO可以作为一个有效的工具，在选择一个在诸如时间和能量等相互矛盾的目标之间进行折中。 此外，最优解对于使用者想学习如何控制变量与过程相互作用非常有用。

1简介

抓斗式卸载起重机用于移动散装材料从船到岸上的料斗。 这种类型的起重机今天通常由使用者控制手推车和抓斗运动使其获得有效的轨迹。 通常通过提升操作方法来改进，本文的想法是相反，使用最佳控制来确定轨迹。然后，最好的跟踪和控制信号可以为了以各种方式改进操作，例如，教导操作员或自主运行起重机。开发和解决最佳控制问题对于起重机已经在几个早期参考文献中进行了研究，参见，例如，Al-Garni et al。（1995）; Auernig和Troger（1987）; Hu和Teo（2004）。

反映起重机的行为成本函数是非常重要的，实现成本函数尽可能好需要选择好轨迹和控制信号。 通常期望的行为是a在不同目标之间的折中，如速度，能源效率，控制利用等目标通常是矛盾的，这意味着依赖关于不同目标的优先顺序，不同轨迹和控制信号将是最佳的。 这里最佳意味着没有办法改善一个客观而不恶化另一个（Miettinen，1999）。满足该属性的解决方案表示为Pareto最优和所有帕累托最优点的集合是帕累托集。 帕累托的形象设置在目标空间表示为Pareto边界。 最佳控制许多目标的问题被称为多目标最优控制问题。

多目标优化控制问题就在论文这里作为一个非线性程序和结果是一个多目标优化问题（MOO）可以写成

有许多算法来“解决”一个MOO。 一个类是标量化方法，另一种是矢量优化方法，参见Miettinen（1999）。 第一类结合形成标量目标函数的目标解决为单目标问题产生一点在帕累托集中的时间。 第二类对待独立的目标，并解决了作为一个向量值优化问题，其中许多点立即获得帕累托集。 在这项工作中，标量化方法已被使用。

除了帕累托最优点如何另一个选择是在什么时候决策者（DM），即：，决定哪个解决方案的人“最好”，做出决定。在本文中，一个互动方法已被选择，其中DM能够 - 在不同的Pareto最优解之间进行选择。以这种方式，DM可以控制对终端的搜索解决方案取决于如何的客观价值和设计变量在Pareto集中变化。选择的过程首选的解决方案也经常是一个好的学习方式关于优化问题和工厂。对于大型，规模问题，如最优控制问题起重机，它可能需要大量的时间来找到一个sin-gle Pareto最优解使用标量化方法并且交互式过程可能是缓慢和繁琐的DM。在最近的研究中，两相方法已经介绍。在这些方法中，帕累托边界是第一个稀疏采样，然后DM能够连续在实际边界的近似上“导航”时间，见Eskelinen et al。 （2010）; Hartikainen et al。 （2011）;Monz et al。 （2008）。然而，在这些方法论文需要一个凸的帕累托边界来产生好近似（工业上并不总是这样过程）或近似的计算可以乏味。在本文中，Linder引入了一种方法et al。 （2012）。通过抽样帕累托并以特定的方式分解该组采样点为凸集，可以进行计算近似Pareto边界快甚至非凸帕累托边界，见Linder et al。 （2012）。

还有其他论文研究了MOO应用于起重机的最佳控制问题，参见例如Deb和Gupta（2004）Logist et al。 （2010），andSakawa和Shindo（1982）。

本文的其余部分组织如下：第2节抓斗式卸载起重机的型号是呈现。 第3节显示如何说明MOO问题从最优控制问题。 第4节介绍开发的MOO框架具有简短的描述的如何可以用来调查帕累托边界。 在第5节框架适用于起重机最佳控制问题。 最后，提出了一些结论在第6节。

2港口起重机的建模

2.1手推车和抓斗

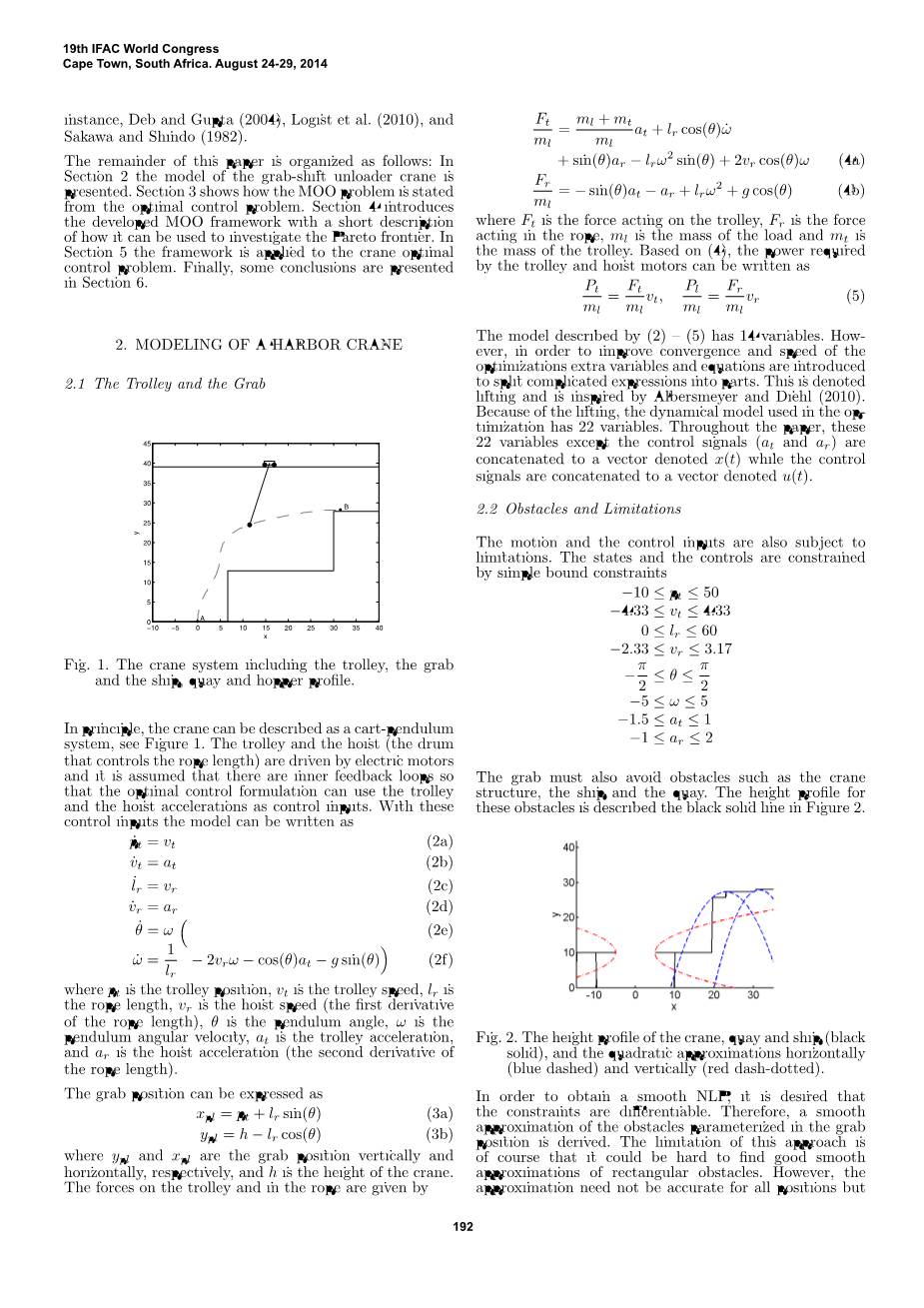
图1 起重机系统包括手推车，抓斗和船，码头和料斗轮廓。

原则上，起重机可以被描述为手推车系统，见图1.小车和提升机（滚筒控制绳索长度）由电动机驱动并且假设存在内部反馈回路等最佳控制公式可以使用手推车和提升机加速度作为控制输入。 用这些控制输入模型可写为：

其中pt）是手推车位置，vt）是台车速度，lr是绳长度r是提升速度（第一导数的绳长度），theta;是摆角，omega;是摆角速度，at）是手推车加速度，和ar是提升机加速度（的二阶导数绳长度）。抓取位置可以表示为

其中ypl和xpl是垂直的抓斗位置水平地，h是起重机的高度。小车和绳索上的力由

其中Ft）是作用在手推车上的力r是力在绳索中起作用l是负载的质量和mt）是手推车的质量。 基于（4），所需功率通过手推车和起重机电机可以写成

1. - （5）描述的模型有14个变量。 怎么样-过去，以提高收敛和速度引入了额外的变量和方程将复杂的表达式拆分成部分。 这被表示并受到Albersmeyer和Diehl（2010）的启发。由于提升，动力学模型中使用的op-timization有22个变量。 在整篇论文中，这些22个变量，除了控制信号（at）和ar） 是连接到表示为x（t）的向量，而控制信号被连接到表示为u（t）的向量。

2.2障碍和限制

运动和控制输入也受制于限制。 状态和控件受到约束通过简单的约束约束

抓斗还必须避免障碍物，例如起重机结构，船和码头。 高度剖面这些障碍物如图2中的黑色实线所示。

图2 起重机，码头和船的高度剖面（黑色实线），以及水平的二次近似（蓝色虚线）和垂直（红色点划线）。

为了获得平滑的NLP，期望约束是不同的。 因此，顺利抓取中参数化的障碍物的近似位置。 这种方法的局限性是当然，它可能很难发现良好的平滑矩形障碍物的近似。 但是，那近似不必对于所有位置准确，而是最佳轨迹经常干扰的位置障碍，通常是角落。 因此，二次功能被选择来代表障碍。 对于码头和起重机是适当的参数化二次函数在水平抓取位置为

其中系数a，b和c通过选择来计算三点使二次函数覆盖角落。 （6）中的约束显示为2条蓝色虚线。

对于抓斗在船外旅行的周期，（6）中的约束就足够了。 然而，在本报告中，我们也研究了抓斗开始和结束时的情况在船内。 对于这种情况，抓斗必须避免船闸门以及因此的附加约束是必要的。 为了方便，这些近似是也表示为二次函数，但参数化垂直抓取位置，

生成的约束显示为2条红色虚线。

3多目标优化控制

3.1最优控制的背景

多目标优化控制可以投射如下

函数F（·）是一个无奇怪的DAE模型，划分包括代数关系的动力学模型，船舶，c（·，·）是附加约束，psi;（·）是终端约束一世是目标，L一世（·，·）是成本函数和tF是最后的时间。

有很多方法来解决最优控制问题，但基本上有两个不同的类别方法即直接或间接，见图3.直接方法意味着控制信号被参数化使用一定数量的参数。结果是无限的包括动力学的三维优化问题方程。动力方程可以在任一方面求解的两种方法。顺序方法，也称为“是指标准优化求解器改变参数，对于给定的参数，dy-使用积分器程序求解命名方程。同时的方法，或基于搭配的方法，上并立即解决了整个问题，因为它是一个大而稀疏的问题优化问题。间接方法是基于Pontryagin最小原理（或变分演算）。这意味着最优化的必要条件最优控制问题，这是一个两点约束，ary问题，使用顺序或a同时方法。优点和缺点的不同方法在Betts中有详细描述（2001）。在本文中，直接同步法是选择。这种方法的一个主要优点是相当一般的约束可以直接处理前进方式。

3.2离散到NLP

对于同步方法，离散化是一个步骤最优控制问题（8）重新表示为a非线性程序（NLP）。 有大量的不同的离散化方法，并取决于它是什么选择，NLP的稀疏模式将是不同的。有关此主题的详细讨论可以在Betts（2001）和Kunkel和Mehrmann（2006）。 在这里纸张第一阶反向偏差公式（BDF）已经用过。 选择第一个的主要动机订单BDF而不是更高阶是第一阶BDF产生最稀疏的NLP和精度解决方案是足够的（高达三阶的评价用于比较）。 解决方案的近似动力系统（8）将使用第一阶BDF，

其中Ts=t）FN和N是离散的数目点。 等式约束cd通常表示缺陷约束。目标也需要离散化离散表达式成为NLP目标。 在这里纸，目标使用标准离散化黎曼总和

对于一般的多目标优化控制问题，MOO NLP生成的就是

3.3目标

在本文中选择了三个重要目标用于分析。 目标是：

bull; F1：最小化一个周期的时间，即：， 的时间从A点移动摆锤的终点到点B.

bull; F2：最小化移动中消耗的总能量。

bull; F3：最小化使用的最大瞬时功率由系统在移动期间。

使用两个第一目标的动机是相当明确。 但是，使用第三个目标的动机可能不是那么明显。 这个想法是，当许多起重机同时操作所消耗的功率如果允许所有起重机，港口将非常大使用大瞬时功率。 港口然后会画大电流从电网是什么港口所有者被收取，不仅是使用的能源由港口。 因此，有趣的是调查是否在周期时间，能量之间存在良好的折衷消耗和最大瞬时功率。

目标函数的数学公式是

其中tF是一个周期的总时间，Pt）和Pl是的分别由（5）给出的吊车和提升电动机功率，和（·） = max（0，·）。 N是时间步长和x的数量是所有决策变量的集合。 因此，能量和最大瞬时功率目标仅被选择考虑加速手推车所消耗的功率抓住并且在制动时不被功率反馈。 积极通过将变量拆分为两部分来重构各部分例如

P = P minus; P minus;, P ge; 0, P minus; ge; 0

重组需要P 和P- 被拉向零，因为否则许多P的组合 和P- - 能够满足P = P - P- - 对于给定的P。 拉动是通过将正则化项添加到（10）中的目标

其中K=1...3,delta;为小数(近似0.001）

4互动MOO的框架

为了计算Pareto边界和导航它，在Linder等人开发的框架 （2012）一直用过的。 基本上，它可以分为两个阶段。

在第一阶段，帕累托边界采样自动方法，行动的DM。 因为它可能需要几分钟甚至一个解决方案，有利的是DM可以无人值守运行这个阶段。 在第二阶段，采样的Pareto集被加载到DM使用的GUI中以在近似的帕累托集上连续导航。

4.1阶段I：相

O ffl in阶段采样完整的Pareto边界均匀。 图4示出了采样的示例R2。这个阶段可以分为三个步骤; 预处理，采样和后处理。

首先，预处理步骤创建搜索方向d和参考点集合zRX。参考中的点

图4 参考点集合（zRX）与方向d在二维MOO的问题。 参考点在等距离之间创建个体最小值z1*：和z2*：。 注意它不是需要参考超平面“高于”完成帕累托边境。

点集用作优化的起点，参见图4.参考点为在由跨越的超平面上等距地创建MOO问题的个体最小值（z1*：和z2*：在图4），方向选择为法线参考超平面。 发现个体最小值将MOO问题划分为一组单目标优化（SOO）问题，以及解决每个目标单独。

其次，采样步骤使用参考点集连同在Pas-coletti和Sera fi ni（1984）来解决MOO问题。对于每个参考点，使用解决SOO问题软件包IPOPT（Wuml;achter和Biegler，2006）。这一步做实际优化找到帕累托边界和取决于样品的数量和大小的MOO问题，这一步可能需要几个小时完成。

第三，后处理步骤应用帕累托滤波器删除所有非帕累托最优解。 为了处理非 - 凸起和断开的Pareto边界在线相位，使用Pareto集分解成单纯形参考点和Delaunay三角测量。 这个使得可以在之间创建线性近似样本，即使Pareto集合是非凸的。

4.2第二阶段：在线阶段

当Pareto集已经获得并分解进入简单，它可以在导航应用程序中打开 - 。 DM使用GUI在采样上导航帕累托通过交互式改变滑块和观看结果实时，见图5.当DM移动时滑块为一个目标，软件瞬间搜索在近似的Pareto集上的解其对应于期望值并且可视化结果，对于目标和决策变量。 它是也可能为DM改变边界目标和决定变量看看如何新约束可能会更改可能的解决方案。

使用分段线性近似的优点的帕累托前沿在线阶段是一个新的可以获得大约Pareto最优解通过求解线性优化问题。 这类优化问题可以解决得非常快

图 5.两个导航应用程序的快照视窗。 a）中显示的第一个窗口显示窗口用于选

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[137094]，资料为PDF文档或Word文档，PDF文档可免费转换为Word