单面通气全尺寸实验研究：风力影响外文翻译资料

英语原文共 9 页，剩余内容已隐藏，支付完成后下载完整资料

---

单面通气全尺寸实验研究：风力影响

Marcello Caciolo, Pascal Stabat , Dominique Marchio

Energy and Buildings 43（2011）1765-1773

摘要：自然通风有助于降低空调需求，并有助于提高建筑物的热舒适度。在本文中，通过简单的自然通风配置（即单面通风）产生的流场和空气变化率进行实验检验。实验是使用几种测量技术在暴露于户外条件的全尺寸建筑物中实现的。对于不同的室外条件（温差，风速和方向），对堆积和风力效应产生的流动的主要特征进行了检验。最后，将测量的空气变化率与通过现有相关性计算的空气变化率进行比较，以分析其对实验配置的适用性。结果表明，风在开口处产生湍流扩散，抵消堆叠效应。此外，在迎风打开的情况下，存在另外的效果，即混合层的效果，这有利于于增加气流速率。现有的相关实验在迎风开启的情况下给出了不错的结果，而在下风口打开的情况下，它们却高估了气流速率。

1. 介绍

自然通风可以提供降低制冷消耗，限制建筑物过热的有效手段，当室外温度低于室内温度（自由冷却）时，通过引入室外新鲜空气，无风扇消耗，即使单面 已知自然通风效率低于交叉通风，这种解决方案在实践中经常被发现，因为它对应于门被关闭的蜂窝办公室或教室的通用空间配置。

单侧通气中通风空气变化率的预测是复杂的，因为开口在入口和出口的同时起作用，给出了每个开口处空气混合和再循环的可能性。

此外，必须考虑到由于风湍流引起的不均匀作用，这在交叉通风中可以忽略。最后，由于整体的风险和风险之间的相互作用而产生的流动路径完全落后。

通过叠加和风力效应的组合，单纯通风所产生的全部空气变化率都有所减少。这些模型通常使用与其建立的相同的实验数据进行验证。与新的实验数据进行比较是必要的，以便测试其适用于更一般的条件和配置。 此外，计算流体动力学（CFD）已广泛用于研究单侧通气。再次，为了提高这种计算技术的信心，与实验数据的比较是有趣的。

本文介绍了在具有单面通气的全尺寸房间中进行的现场测量，暴露于真实的室外条件下，使用多种测量技术。然后，对实验结果进行分析，以便更好地了解叠层和风力影响产生的流动机理。最后，将实验空气变化率与现有经验相关性的预测值进行比较，以评估其强度和极限。

1. 检查单面通风换气率的现有相关性

文献中提出了个别经验相关性，以便计算由于堆叠和风力影响的组合而引起的气流速率。

Warren提出了两种表达方式：一种用于堆叠驱动的单面通气，基于分析考虑;另一种用于风力单向通风，基于在两个全尺寸建筑物中进行的实验:

在两个方程中，q堆和q风分别是由于堆和风而引起的气流速率，Cd是排放系数，通常取0.6，Aeff是开口的有效流动面积，Delta;T是户外室内温差，H为开口高度，g为重力加速度，Tav为户外与v风之间的平均温度为风速。

在堆叠和风力效应的组合的情况下，Warren提出分别计算每个参数的影响，然后使用其中最大的。

Pfaff和De Gids提出了一个经验表达式，基于全尺寸建筑物的33次测量，适用于组合风和堆叠效应的情况：

其中因子1/2来自于空气仅流过开口的一半并且veq是开口处空气的“等效速度”，计算公式为：

其中C1，C2和C3是经验系数。平方根下的三项分别对应于由风，浮力和湍流引起的压力差，这被认为是加法的。

使用类似的方法，Larsen和Heiselberg得出了一个考虑到风向的更为复杂的相关性。在几次风洞试验的基础上建立的表达形式如下：

其中C1和C2是取决于风向的经验系数，f（beta;）和Delta;Cp,opening(beta;v)是风向的经验函数，Cp是开口处的风压系数。

最后，Dascalaki等人认为，像COMIS这样的多区域气流模型在单面通气预测中没有考虑到风力影响。因此，基于52次全面实验，它们定义了一个校正因子 可以应用于气流模型的结果，使用1作为排放系数以考虑风力影响：

表1：

单面通气计算气流率的现有相关性

表1总结了不同作者提供的表达式，用于计算由堆叠效应引起的空气变化率，风力效应及其组合。

1. 实验装置

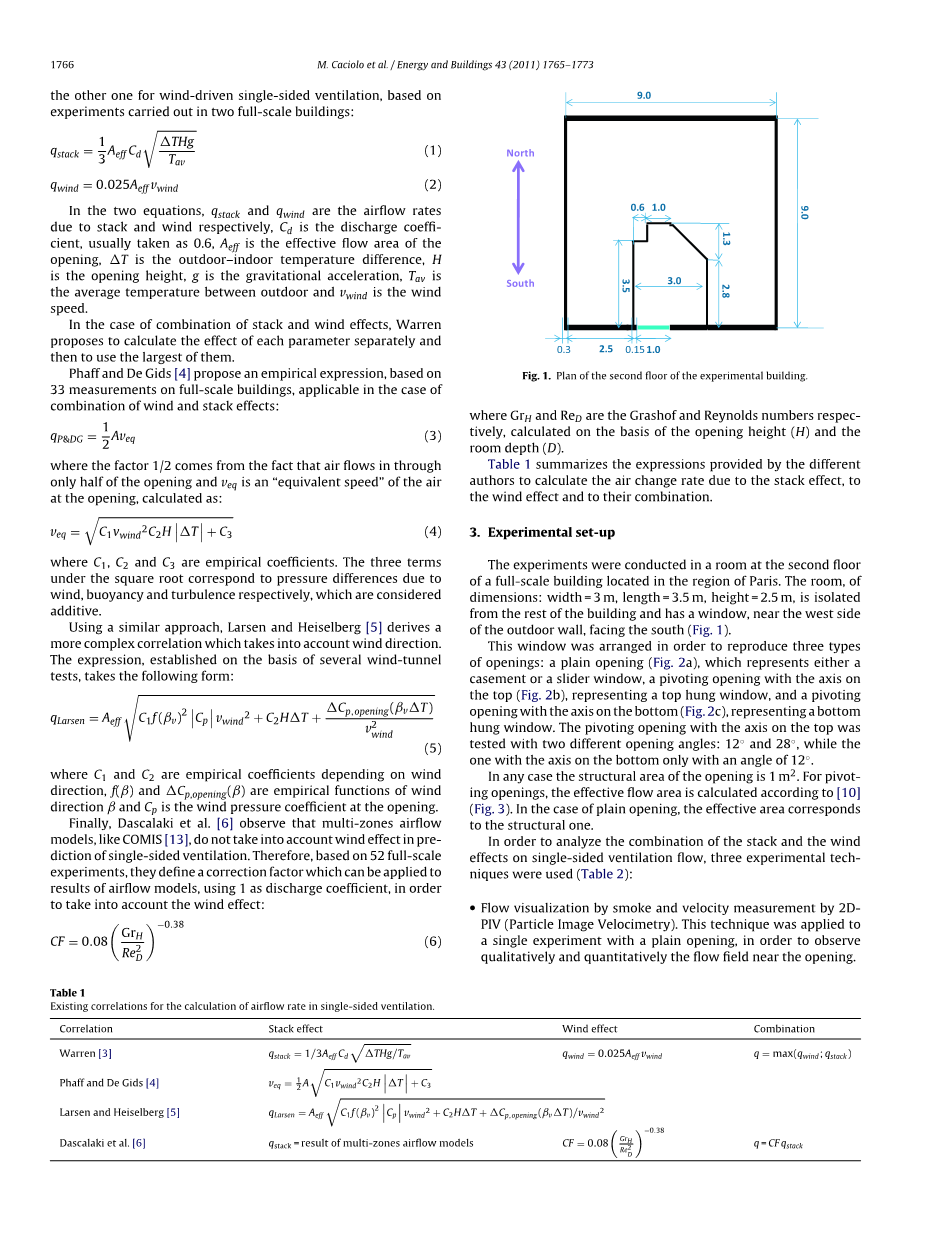
图1：实验楼二楼计划

实验在位于巴黎地区的全面建筑二楼的一个房间进行。 尺寸：宽度= 3m，长度= 3.5m，高度= 2.5m的房间与建筑物的其余部分隔离，并且在室外墙的西侧附近有一个朝南的窗户（图1）。

这个窗口是为了再现三种类型的开口而设置的：一个平面开口（图2a），它表示一个窗扇或一个滑动窗口，一个位于顶部轴线的枢转开口（图2b），代表顶部悬挂窗口和具有底部轴线的枢转开口（图2c），表示底部悬挂窗口。测试顶部轴线的枢转开口有两个不同的开启角度：12◦和28◦，而底部轴线的角度为12◦

在任何情况下，开口的结构面积为1m 2。对于旋转开口，根据（图3）计算有效流动面积。在平开的情况下，有效面积对应于结构。

图2：打开配置通过实验测试：平面打开和枢转开口，顶部和底部均为轴

图3：计算枢转开口的有效流动面积

图4：用于实验的PIV系统的示意图

为了分析叠层和风力对单侧通风流的影响，采用了三个实验技术（表2）：

表2：实验技术使用

• 通过2D-PIV（粒子图像测速）的烟雾和速度测量的流动可视化。将该技术应用于具有平开口的单个实验，以便定性和定量地观察开口附近的流场。
• 热风速测量法。在开口平面上的不同点测量速度，湍流速率和温度，以找出这些量与室外条件之间的关系。
• 气体示踪剂衰减技术，为了测量室内不同室外条件下的空气变化率。

在每个实验中，平均室内温度由位于房间不同位置的六个PT-100传感器测量（精度：plusmn;0.1℃）。 户外条件，即风速和方向，室外温度和总太阳辐射，由位于10米高（屋顶高度）的当地气象台进行监测。

• 1. 2D-PIV

2D-PIV用于测量垂直于其前面开口的垂直平面上的流场。 PIV系统由双腔Nd-Yag Solo III激光器组成，其产生照亮测量平面的光片，以及垂直于测量平面定位的CCD相机FlowSense 2M（Dantec Dynamics）。CCD摄像机在短时间内记录了几个图像，由软件包“Dynamic Studio”处理，以计算播种颗粒的位移，从而计算出速度场。

• 1. 热风速计

空气速度和湍流通过五台Schiltknecht ThermoAir6热球风速计测量，该风速计独立于频率为10Hz的流量方向测量风速。速度在5分钟内平均。湍流速率作为瞬时速度的RSM值在5分钟内计算。此外，温度也通过温度探针安装在一起，以1Hz的频率进行测量。

风速计位于开口的平面上，如图5：

图5：热风速计在开口处的位置（从外部看）

• 1. 气体示踪剂衰变

通过气体示踪剂衰减技术计算通风空气变化率。所用的气体示踪剂是SF6。SF6的浓度通过基于光声红外光谱的B＆K型1302气体分析仪测量。分析仪连接到房间的两个采样点。采样周期约为1.5min，两个浓度 采样点每3分钟测量1次。

在每次实验之前，将SF 6注入房间而不打开窗户，以实现均匀浓缩。通过使用桌面风扇来增强混音效果。当两个采样点测量的SF 6浓度变得均匀时，停止注入气体。然后，窗口打开，并监测气体示踪剂的衰减（图6）。

图6：示踪气体测量的空气变化率的确定

浓度衰减由下式表示：

其中C(t)和C(t 0)分别是时间t和初始时间的浓度，N是空气变化率。

通过在20分钟内浓度时间历史的对数的线性回归，对每个采样点计算N的值。房间的变化率计算为两个采样点计算的变化率的平均值。

计算出的交换空间的不确定度估计为plusmn;25％。

1. 结果分析：风和堆叠效应

自然通风的驱动力是温度差异（堆积效应）和风力影响。由堆叠效应驱动的单面自然通风只得到了广泛的分析。相反，缺乏关于堆叠和风力效应的组合的信息。

本节主要分析实验结果，以了解风效应如何影响堆叠效应产生的流场。

• 1. 风对流场的影响

当只有堆叠效应发生作用时，流动是双向的，中性平面水平（NPL）位于开放的一半高度.Heiselberg等人通过烟雾测试来查看开口附近的流场，以获得较大的温差 （20°C），无风。空气流过窗帘的下半部分，并形成一个稳定的喷气，低速流向地板。

为了定性地了解风对流场的影响， 图7示出了平开的情况下,流场的烟雾可视化，温差为7℃,风速为2.5m/s，风向为东南风（迎风）。

流场与Heiselberg等人观察到的相似，除了在这种情况下，喷气机呈现出较大的扩散，这是由于湍流空气引起的，这进一步增加进入和离开空气之间的空气混合（湍流扩散）。

此外，由于风湍流，喷气式飞机的大小和形状都有快速的波动。 这些波动也是通过PIV可视化观察到的，其显示出高度不稳定的速度场。然而，当在3分钟的时间段内平均时，速度场显示类似于没有风的情况的行为（图8）。

实际上，如在质量上观察到的，平均流场与仅由堆叠效应而变化的平均流场非常相似，在开口半高处流动反转。对于这个低风速（2.5m/s），平均流速值开口前面的平面相对较低，为0.1-0.2m/s。

图8：PIV测量开口前的平均流场

• 1. 风速对开度的速度，湍流和温度影响

烟雾和PIV的测量表明，对于低风速，开口附近的流动是湍流，主要是堆叠效应，其特征是平均速度相对较低。为了将这些结果扩展到更高的风速，几个实验是实现测量空气速度，湍流和开口处的温度。

图9显示了图5的五个测量点作为风速的函数的平均速度和湍流速率。

风速增加的第一个影响是开口处的平均空速成比例地增加。然而，重要的是精确地说，我们不能直接将这种增加与气流速率联系起来，因为只有垂直于开口区域的速度分量有助于换气率。

另外，随着风速的增加，湍流速率也随之上升。因此，我们预期以前观察到的流动的湍流扩散和不稳定性随风速而增加，从而改善进入和离开空气之间的空气混合。

为了确认这种混合，可以观察开放时的有效温差的变化。实际上，在没有湍流扩散的情况下，开口的顶部和底部之间的温差相当于开口的温差，即室外-室内温度差。相反，因此湍流扩散增加，进入和离开房间的空气之间混合。由于这种混合的结果，预期开口处的有效温差，从而堆积效应降低。

图10展示了开口处的非二维有效温度梯度（Delta;T*）与风速之间的关系。

有效温度梯度定义为开口顶部和底部（T1 T5）/2-（T2 T6）/2（见图5）之间的温差，这导致堆积效应。该量除以室内和室外的温差，得到无量纲温度梯度Delta;T*。

无量纲温度梯度与风速成反比，确认了开口处的空气混合。

图9-10中结果的大幅度扩展是由于风向和其他室外参数的影响，尽管尚未找到对这些因素的明确依赖。

图9：作为风速函数的开口平面中的平均速度和湍流

图10：作为风速的函数，开口处的无尺寸有效温差。

• 1. 混合层

在风的存在下，与空气变化率相关的重要影响是混合层。 当开口附近的局部速度平行于墙壁时，即开口处是风区时，出现混合层（图11）。在这种情况下，当到达开口的上游边缘时，室外空气渗入房间 ，夹带室内空气并与之混合。 当到达下游边缘时，部分混合空气进入房间。 这种机制提供室内和室外空气之间的交换。

图11：混合层示意图

混合层的存在可以通过开口两侧的空气流速进行调查。 实际上，混合层的上游流动的特征在于比下游流动更低的空气流速（图12）。 图12显示了西侧的速度（探头6，见图5）和东侧（探头2）之间的关系，两个实验子集：从东南风向（蓝色标记）和实验表征的实验 其特点是从北方风向（红色）。

图12：由探头6测量的空气速度作为探头2在开口处测量的空气速度的函数。

在东南风的情况下，开口西侧测量的空气速度（探头6，下游）高于西侧（探头2，上游）测得的空气速度，证实存在混合层。

对于北风（迎风），开口两侧测量的空气流量是相同的。另外，在背风开启的情况下，空气流速远低于迎风开启的情况。 可以通过考虑风在建筑物的背风侧形成大的再循环区，其特征在于低气压（图13）。 因此，在这种情况下混合层的效果可以忽略不计。

图13：在背风开启的情况下，围绕建筑物的气流模式的示意图

• 1. 风对空气变化率的影响

在没有风的情况下，即仅当堆叠效应起作用时，可以分析地导出气流速率。

为了了解上一节（湍流扩散混合层）确定的风力影响气流速率，现分析空气变化率实验结果。

实验分为两组（图14）：迎风试验，西南风，背风实验，东风风。

两组实验都呈现出很好的温差变化范围（2°C和9°C之间的Delta;T）和风速（2-5.5m / s）

图1

剩余内容已隐藏，支付完成后下载完整资料

---

资料编号：[137104]，资料为PDF文档或Word文档，PDF文档可免费转换为Word