英语原文共 10 页,剩余内容已隐藏,支付完成后下载完整资料
一种基于三相二极管整流器的功率因数校正技术
A.R. Prasad,IEEE会员,Phoivos D. Ziogas, IEEE高级会员,Stefanos Manias
本文收稿于1989年4月4日,是在1989年6月26日-29日期间于密尔沃基举行的IEEE电力电子专家会议上提出的。
摘要:本文提出和分析了一种新型的基于带有前端三相二极管整流器的电源的有源功率因数校正方法(图1)。这种方法的实施需要使用一个额外的单开关升压斩波器。合并后的前置整流器绘制出的从交流电源处得到的正弦交流电流的输入功率因素接近1,同时工作在一个固定的开关频率上。此外,本文表明,当有源输入功率因数校正阶段也被用来调节转换器的直流母线电压时,与传统的三相交流-直流转换器相比,本文所述的转换器的性能得到了改进。这些改进包括减少了元器件的个数,简化了输入同步逻辑要求,和只需要更小的无功分量。最后,这些理论结果已经被实验证实了。
Ⅰ、简介
传统地,公共基础设施中的交流线路的电压转换主要是相位控制或二极管整流器来实现。经过这个整流器得到的输入电流会对配电网络和其它相邻电力系统的整流器造成一系列的问题,包括:
- 电流和电压的相移要求电源和配电设备处理无功功率,提高其视在功率;
- 较高的输入电流谐波畸变率和较低的输入功率因数;
- 降低整流效率,由于输入电流的有效值较大;
- 输入的交流电源电压失真,由于相对应的更高的峰值电流;
- 需要更大尺寸的无功元件。
为了克服这些缺点,系统设计人员越来越多地融合各种有效的提高输入功率因数的校正方法[2]-[4]。对于中高功率的应用而言,它们的输入整流器是靠三相交流电源供电。旨在提高三相交流-直流转换器功率因数的Bang-Bang滞环控制方法的应用,已经被几位作者讨论过了[2]-[4]。在这些参考资料中,三相交流-直流转换器已经通过采用适当输入输出连接的三个单相交流-直流转换器(图2)实现了。这种拓扑结构产生单位输入功率因数,而且明显远远优于原来的相位控制的AC - DC拓扑结构。然而,它也表现出一些缺点,包括;
1)需要复杂的输入同步逻辑;
2)由于功率电路中三个单相转换器控制参数的变化,由输入线电流(Iia)产生的三次谐波无法被完全消除;
3)开关频率依赖于负载;
4) 三相交流-直流转换器所需要的元件数量是单相交流-直流转换器的三倍;
5)使用三相逆变器和变压器(更好的变压器铁心和铜的利用率等)的优点是无法实现的。
本文讨论了三相交流-直流转换器的分析方法和设计过程,它能够从交流电源处得到高质量的输入电流波形,而且没有表现出前文提到的缺陷。然而,它存在着大大增加开关器件的电流承受力和前置滤波交流输入电流的高频率谐波。关于提到的转换器的工作原理将在下一章讨论。
Ⅱ、工作原理
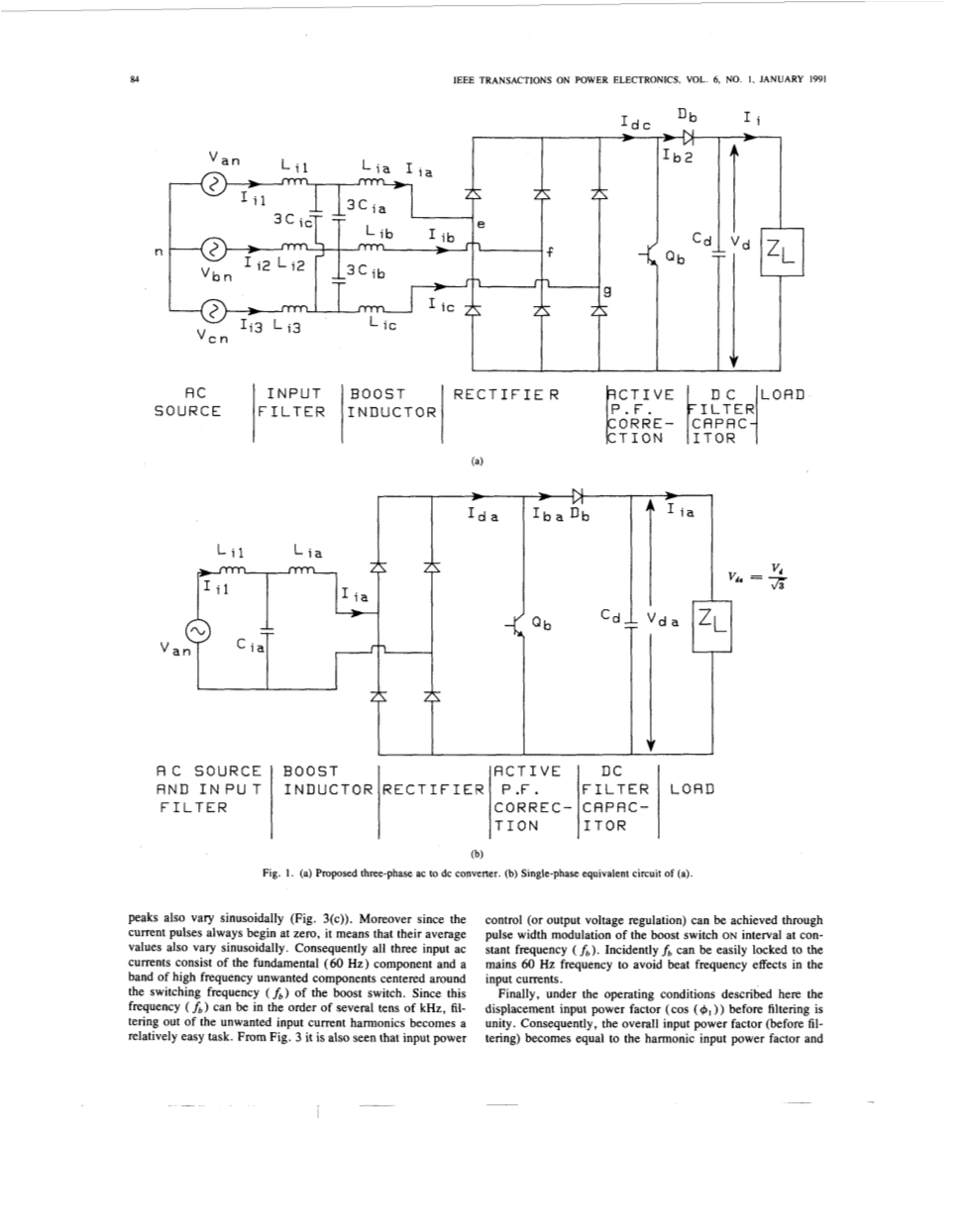
前文提到的三相交流-直流转换器(图1)由两个主要的功率转换阶段构成。第一阶段是一个由输入滤波器、升压电感、三相二极管整流器、有源功率因数校正和直流滤波电容器组成的阶段。第二阶段可以被建模为任何类型的负载,它需要一个受控或不受控的直流母线,例如通用的单相逆变器或三相逆变器或带有高频隔离的直流-直流转换器。输入电流波形的有源形成是通过使用三个升压斩波元件Lia,Qb,Db得到的,如图1所示。升压开关Qb工作在恒定的频率。QB的占空比随着负载的不同而不同,因此它的输入电流是不连续的。当升压开关处于导通状态时,所有三个输入交流相位因通过电感Lib,Lib,Lic,六个整流二极管和升压开关而变小。因此,三个输入电流Iib,Iib,Iic开始同时以一定的速率增大至与各自相电压对应的瞬时值。此外,在每个导通间隙的特定峰值电流值与它们在相同导通间隙内对应的输出相位电压的平均值成比例。由于这些电压平均值呈正弦性变化,所以输入电流的峰值也呈现出正弦性变化(图3(c))。此外,由于脉冲电流始终为零,这意味着他们的平均值也是呈现出正弦变化。因此,所有三个输入交流电流由基础(60 Hz)组件和不想要的一个高频率带宽在升压开关的开关频率(fb)附近的元件组成。因为这个频率(fb)可以达到几十kHz,所以过滤掉不需要的输入电流谐波变成是一个相对容易的任务。从图3还可以看出,输入功率控制(或输出电压调节)可以通过控制脉宽调制升压开关在恒定频率(fb)的导通时间来实现。顺便说一句,fb可以很容易地锁定到60HZ的频率以避免受到输入电流频率的影响。
升压电感
负载
直流滤波电容
有源功率因素校正
整 流 器
交流
电源
输入滤波
(a)
交流
电源以及输入滤波
交流
电源以及输入滤波
负载
直流滤波电容
有源功率因素校正
整流器
(b)
图1.(a)三相交流-直流转换器.(b).图(a)的单相等效电路
最后,在这里描述的工作条件下,位移输入功率因数(COS(phi;1))在过滤之前是为1的。因此,总的输入功率因数(滤波前)变得与谐波输入功率因数相等,即为:
功率因素= (1)
当Iia,n是电流Iia的傅里叶变换的n次谐波分量,COS(phi;1)是位移因素。
值得注意的是,电流谐波以及它的功率因素可以通过一个相对小的输入电容(Cia)和电感(Li1)的高频率抑制住。因此,过滤后的整体输入功率因数(即交流源)是非常接近与1的。
直流滤波电容
负载
有源功率因素校正
滤波器
交流
电源以及输入滤波
升压电感
图2.传统的三相交流-直流变换器
Ⅲ、输入电流分析
对于图1所示的阶段,当升压开关(Qb)处于导通状态时,等效单相电流变得如图4(a)所示。输入电流Iia的上升频率由输入电源电压和电感决定。电流(Iia)在这个阶段(beta;le;tle;t1)通过电感时有以下关系:
为了解得上述公示的中的Iia,带入初始条件,Iia(omega;t)=0,t=beta;时有
当beta;的大小刚好能够使升压开关(Qb)导通时,参照的输入电压Van和t1也处于升压开关(Qb)的导通状态。当处于升压开关(Qb)断开的阶段时,流过电感的电流的下降速率由输入电压(Van)、输出直流电压(Vd)和电感(Lia)的大小决定。这种情况下的单相等效电路如图4(b)所示。对于图4(b)所示的升压变换器理论,当升压开关断开时,滤波器的输入相电压(Ven)为
式中D是升压开关(Qb)的占空比。当处于升压开关断开的状态时,t1le;tle;t2,流过电感(Lia)的电流(Iia)为
将初始条件当t= t1时,Iia(omega;t)= Iia(omega;t1)代入(4)时解得Iia,
对于设计者而言,最坏的工作情况就是恰好在当输入电压达到峰值时(Van(peak))连上升压开关(Qb)。在这种情况下,流过电感(Lia)的电流以最大速率增加,并在t1的末端达到最大值。同时,也是在这种情况下,电流(Iia)降至0所需要的时间最大。因此,升压开关(Qb)的频率是交流输入电压(Van)和输出直流电压(Vd)的函数。将beta;=90°,t=(90° t)带入式(2)可得
图3.仿真波形.(a)三相交流电源相电压。(b)升压开关(Qb)门控信号。(c)整流器输入电流(Iia)及其频谱。(d)整流器输出电流(Idc)及其频谱。(e)三相二极管整流器开关函数及其频谱。(f)升压二极管(Db)开关函数及其频谱。(g)升压开关(Qb)端电压。
图3.(续前图)
实际上,升压开关频率fb的大小在20-40Khz,而且与在输入电源电压(Van)时间段相比,fb在升压开关导通阶段(t1)的值更小。当omega;t的值较小时,sin(omega;t)的值近似于omega;t。因此,式(6)可变为
当t1时,电感电流(Iia)达到最大值,升压开关(Qb)受适当的控制信号的影响而关闭。将beta;=90°,t=(90° t)代入式(5)得
并将omega;t代入sin(omega;t),上述等式即可化为
图4.(a)当升压开关导通时的等效单相电路。(b) 当升压开关断开时的等效单相电路。
在t=t2时,电流Iia(omega;t)=0,将这个条件代入上述公式可得
因此,输出直流电压的最小值
如果直流输出电压(Vd)小于上述所说的值,则电感电流(Iia)就会在此刻减小至0。所以,升压开关频率需要减小至某个值,此时电感电流(Iia)会在升压开关(Qb)再次导通前变为0。换句话说,升压开关的占空比必须减小至给定的升压开关的开关频率(fb)。因此,升压开关的开关频率(fb)是直流输出电压(Vd)的函数。最小直流母线电压(Vd)随升压开关的占空比的变化如图5所示。
经以上阐述可知,模拟电感电流(Iia)及其频谱,二极管整流器开关函数(Sd(omega;t))及其频谱,二极管(Dd)开关函数(Sd1(omega;t))及其频谱都可推导出来,并如图3所示。图3清晰地展示了整流器的输入和输出电流(Iia,Idc)经低频元件滤波后的波形。
输入电流(Iia)的表达式可以通过傅立叶变换获得
An和Bn是电流(Iia)的傅里叶变换系数。上述表达式可以进一步简化成
当
Cn和theta;n的值取决于特定电感值(Lia)下的升压开关的工作频率。输入功率因素(没有输入滤波)随升压开关占空比的变化关系如图6所示。低输入功率因素是由于电流(Iia)中高频率谐波的存在引起的。这些高频率电流谐波可以用一个小的输入滤波器滤掉,以此使得输入功率因素接近于1。峰值输入电流(Iia)取决于电感(Lia)的值、工作频率以及升压开关的占空比。
Ⅳ、系统分析
在本章节中,先前提到的转换器将在静态条件下分析。推导出的表达式将在下文中为设计合理的转换器提供必要的信息。转换器将在以下几个假设的基础上分析:
- 所有电源开关设备都是理想的,并且二极管的正向压降和反向漏电流可以忽略不计;
- 滤波元器件是理想的;
- 电压没有纹波。
而且,额定输入电压的有效值Van(rms),以及额定输入功率Pd被假设成
进一步假设交流电源频率角是1.0(标幺值),从图3(c)可知当Lia=0.1(标幺值)时,峰值电流Iia(peak)为
Tb升压开关的时间周期。电流基波分量Iia.1的振幅为0.62。从式(13)可知电流Iia的峰值取决于Lia、Van(peak)以及Tb的值。从图3(c)可知电流Iia.1(peak)与Iia(peak)的比值是0.418。因此电流Iia.1(peak)的通用表达式为
在所有升压开关的开关频率下,电感Lia的最大值均可通过式(14)计算。
-
整流器输出电流的推导及输出滤
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[137128],资料为PDF文档或Word文档,PDF文档可免费转换为Word
课题毕业论文、外文翻译、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。