英语原文共 9 页,剩余内容已隐藏,支付完成后下载完整资料
基于增益和相位裕度的多回路PI
控制器整定
Zhuo-Yun Niea,b,Qing-Guo Wangb,*,Min Wua,Yong Hea
a中南大学信息科学与工程学院,长沙410083,中国
b新加坡国立大学电气与计算机工程系,新加坡119260,新加坡
摘 要
在本文中,提出了一种单循环策略来设计多回路PI控制器来实现两输入和两输出(TITO)进程中所需的增益和相位裕度。为了处理回路的相互作用,TITO系统被转换成具有从交互中得到的不确定性的两个等效单个循环。在一个回路中对初始控制器设计估计最大不确定度,并且应用单输入和单输出(SISO)控制器设计。该控制器代替其他等效回路进行设计,最后,第一回路控制器根据其他回路控制器的知识进行改进。对于SISO控制器整定,提出了一种新方法来确定可实现的增益和相位裕量以及相关的控制器参数。本文将给出实例用于比较和说明。
关键字:控制器整定,PI控制器,增益和相位裕度,TITO系统过程
1.引言
增益和相位裕量通常用作整定SISO工业系统PID控制器的性能规格[1-3]。其中主要原因是增益和相位裕度已经作为控制环路中的稳定性和鲁棒性的重要度量,不像Hinfin;,H2,l1和mu;方法往往导致控制器脆弱[4]。在由于Astrom的[5]方法的公知设计过程中,极限增益和频率通过继电器测试和用简单公式计算的控制器估计。 Ho等[6]提出了一种基于简化的一阶加死区时间模型的调谐方法。 与这种简单模型不同,Fung等人[7]提出了一种用于任何线性系统的PI控制器整定的图形方法,其中可以实现精确余量,而不管过程顺序,时间延迟或阻尼特性。然而,这种方法可能没有解决方案,除非增益和相位裕度在获得解决方案之前被适当地选择。
工业中的大多数过程具有多输入和多输出(MIMO)性质。 分布式控制在MIMO系统中很流行,因为它具有简单的结构和较少的调整参数来处理[8,9],并成为一个活跃的研究课题多年[10-12]。独立设计和顺序设计是分散控制的两种常用设计策略[13-15]。 但前者忽略环间相互作用,而后者需要大量的SISO设计迭代。MIMO分散控制设计是复杂的,因为控制回路之间的相互作用[16],特别是对于增益和相位裕度规范,甚至SISO通常情况没有解析解。在MIMO增益和相位裕量的情况下,Ho等人[17]提出了基于Gershgorin带的整定方法,并且SISO增益和相位裕度设计被应用于每个环的频带。然而,Kookos [18]指出,这种方法只有在开环系统是主导时才有效。Huang等人[19]使用等效单环与有效开环过程(EOP)来推导多环PI / PID控制器。 在这种方法中,为获得EOP进行模型缩减和近似是必要的,这样带来的设计误差是不可避免的。在本文中,我们开发了一个单迭代策略来为TITO过程设计控制器,这是工业中最常见的多变量系统[20,21]。 我们基于未知的第二回路控制器的一些不确定性估计而在一个回路中设计初始控制器; 然后用已知的第一回路控制器设计其他回路的控制器; 最后,我们用已知的第二回路控制器重新调整第一回路控制器。利用其他回路控制器的参数,一个回路的等效过程可用SISO设计处理。 在本文中,我们还提出了一种新的SISO PI控制器整定方法,以确定可实现的增益和相位裕量以及相关的控制器参数。
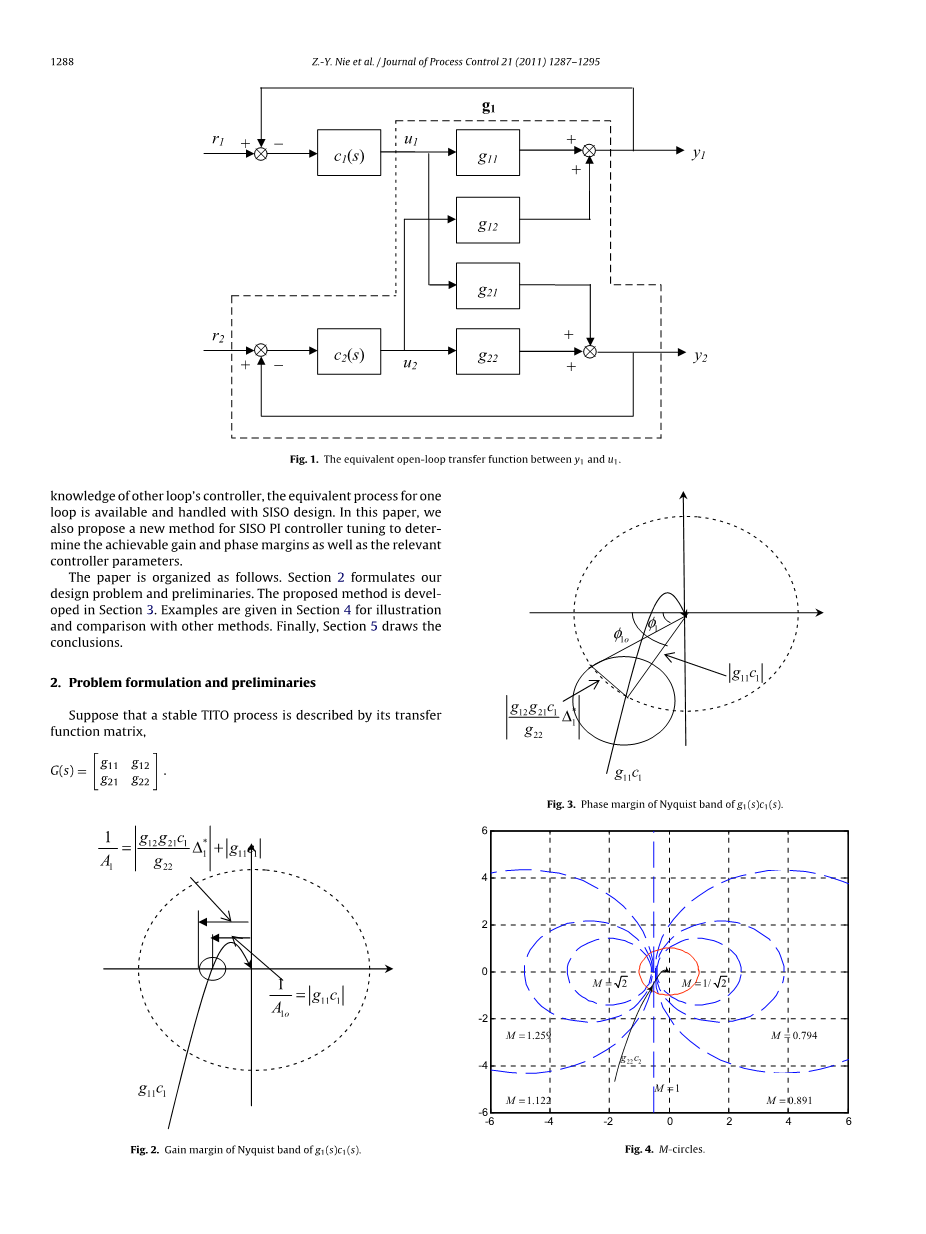
图1. y1和u1之间的等效开环传递函数
本文的结构如下。 第2节说明我们问题的提出和初步方案。 所提出的方法在第3节中实践。在第4节中给出用于说明和与其他方法比较的案例。 最后,第5节得出结论。
2.问题的提出和初步方案
假设稳定的TITO过程由其传递函数矩阵描述
图2 g1(s)c1(s)的奈奎斯特幅值裕度
图3 g1(s)c1(s)的奈奎斯特频相位裕量
图4 M圈
图5单位输出反馈系统
图6直线和半圆的交点
图7可实现的增益和相位裕量
图8 PI控制器的参数
图9所得系统的伯德图
图10实施例1的阶跃响应
它在图1所示的单位输出反馈配置中由对角线的常规PI控制器控制
,
图11 回路1的奈奎斯特频带(3)可实现的幅值和相位裕度
图12 回路1的初始PI控制器c1(s)参数
图13 回路2可实现的幅值和相位裕量
图14 回路2的PI控制器c2(s)参数
图15 回路1可实现的幅值和相位裕度
图16 回路1的PI控制器c1(s)参数
图17 g1(s)c1(s)的奈奎斯特曲线
图18 g2(s)c2(s)的奈奎斯特曲线
其中每个控制器被参数化为
从图1可以看出
当第二回路闭合时,即u2 = - c2(s)y2,y1和u1之间的等效开环传递函数由下式给出
(1)
类似地,y2和u2之间的等效开环传递函数由下式给出
(2)
使两个环路的期望增益和相位裕度分别为(A1,phi;1)和(A2,phi;2)。由于控制回路之间的相互作用,上一节中提到的SISO控制器整定方法不能直接使用。 例如,由于存在未知控制器,等效过程(1)变为不确定的工厂。 类似地,当为等价过程(2)应用到c2(s)的设计时,存在未知控制器c1(s)。 为了打破这种相互关系,让我们优先考虑式(1)。令
我们将其视为不确定性,并将其最大幅度表示为△*1。 我们会估计。 然后,回路1的开环传递函数由下式给出
(3)
其奈奎斯特曲线将由奈奎斯特频带实现,奈奎斯特频带分别由中心和半径为g11(jomega;)c1(jomega;)和|(g12(jomega;)g21(jomega;)c1(jomega;)/g22(jomega;))△*1|的圆形成,注意,g11(s)c1(s)的奈奎斯特曲线是奈奎斯特频带(3)的中心线。图2和图3显示出了对角元素g11(s)c1(s)及其不确定性圆的典型奈奎斯特曲线。首先,我们假设(3)的奈奎斯特频带上的增益和相位交叉频率及其中心曲线g11(s)c1(s)彼此相同,这与Ho的情况[17]是相同的假设, 但将仅用于初始控制器设计。 这意味着
- ang;g11(jomega;p1)c1(jomega;p1) = minus;pi;,其中omega;p1是奈奎斯特频带(3)上的相位交叉频率;
- |g11(jomega;g1)c1(jomega;g1)| = 1,omega;g1是奈奎斯特频带(3)上的增益交叉频率。
3.提出的方法
在我们的设计策略中,我们基于由于未知的第二回路控制器的一些不确定性估计而在一个回路中设计初始控制器; 然后用已知的第一回路控制器确定第二回路控制器; 最后,利用已知的第二回路控制器重新调整第一回路控制器。
在不失一般性的情况下,让初始控制器处于环路1.目标是形成奈奎斯特频带(3)以实现增益裕度A1和相位裕量phi;1。 分别用A1o和phi;1o表示对角线环路的增益和相位裕量g11(s)c1(s)。 从(3)和图2可以看出,A1可以用A10表示为
(4)
并且类似地从(3)和图3可以看出,phi;1以phi;1o表示
(5)
方程(4)和(5)表明,形成奈奎斯特频带(3)以满足A1和phi;1的初始控制器的设计等效于使g11(jomega;)c1(jomega;)的奈奎斯特曲线形状具有A1o和phi;1o:
(6)
(7)
这样,环路1的初始控制器设计成为(6)和(7)中的标准SISO PI控制器设计问题。
通过将初始控制器代入(2),等效开环过程g2(s)可用于知道c1(s),并且应用SISO设计以获得用于环2的c2(s),以满足增益裕量A2和相位裕量phi;2,
(8)
(9)
最后,将c2(s)代入(1)并且在知道c2(s)的环路1中重新设计新的c1(s),以获得增益裕度A1和相位裕量phi;1,
(10)
(11)
在上述设计过程中,c1(s)必须设计两次。 第一次是第一次,第二次是最后一次。 为了设计初始的,我们使用奈奎斯特带的包络曲线(3)。 虽然这个设计步骤本质上是保守和近似的,但它有助于在其他循环中获得c1(s)而不知道控制器; 此外,该初始控制器c1(s)不仅稳定等效处理(1),而且使所得到的真实环路具有接近期望增益和相位裕度的增益和相位裕量。我们的模拟研究表明,c1(s)的初始控制器和最终控制器通常有非常相似的动态行为。因此,基于重新设计的c1(s)重新调谐第二等效回路的c2(s)具有有限的规格改进,并且不需要,参见下一节中的模拟结果。因此,我们的设计能够 仅在一次迭代之后停止。
图19 例2的闭环时间响应
表1 控制器参数和得到的实施例2的性能指数
3.1最大不确定度的估计
上述设计的关键因素是估计由于未知c2(s)引起的不确定性△1(s)的最大幅度△1*。 看看△1(s)=(g22(s)c2(s)/(1 g22(s)c2(s)))的形式,这促使我们研究方程的性质:
(12)
如图4所示,M的不同值的z的轨迹被绘制在复平面中,其通常被称为M圆。可以看出,Mgt; 1的所有那些M圆位于Re(z)lt;-1 / 2的平面处,并且圆随着M增加而变小;另一方面,所有这些具有0 lt;M lt;1的M-圆位于Re(z)lt;-1 / 2该圆随着M减小而变小。
通常,g22(s)c2(s)(或z的轨迹)的奈奎斯特曲线从正实轴开始并移动到单位圆,|△1(s)| (或M)增加。 然后,奈奎斯特曲线(或z的轨迹)落入单位圆中并且倾向于以|△1(s)| (或M)减小。 因此,最大|△1(s)| 大约当| g22(s)c2(s)|时实现 = | e(-pi; theta;)j | = 1,其中theta;是g22(s)c2(s)的相位裕量,这意味着 △1*可近似取为
(13)
注意,g22(s)c2(s)的奈奎斯特曲线总是与g2(s)c2(s)的奈奎斯特曲线一起旋转,并且g2(s)c2(s)的合理相位裕度通常在45°和90°。 因此,我们采取g22(s)c2(s)在45°和90°之间,也给出了△1*isin;(0.707,1.3066),默认值为1。
3.2 PI控制器设计用于SISO案例
Fung等人的[7]图形方法看起来适用于这里。 然而,它们的方法要求用户事先指定合适的增益和相位裕量以实现解决方案,或者调整规格直到找到解决方案。 我们在这里开发了一
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[137172],资料为PDF文档或Word文档,PDF文档可免费转换为Word
课题毕业论文、外文翻译、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。